河南省豫东名校2022-2023学年上学期理数新高三摸底联考试卷

这是一份河南省豫东名校2022-2023学年上学期理数新高三摸底联考试卷，共21页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（共12小题，每小题5分，共60分）
1．设全集U=R，若集合A={−1，0，1，2，3，4，5}，B={x||x−2|>1}，则集合A∩(∁UB)=（ ）
A．{1}B．{−1，0，4，5}
C．{1，2，3}D．{0，1，2，3}
2．已知复数z=a+bi(a，b∈R)，若ai2022+2i=1+bi，则|z|=（ ）
A．2B．3C．2D．5
3．已知平面向量a，b满足a=(3，1)，|b|=2，|a+b|=2，则a与b的夹角为（ ）
A．2π3B．π4C．3π4D．5π6
4．“中国剩余定理”又称“孙子定理”，1852年英国来华传教士伟烈亚利将《孙子算法》中“物不知数”问题的解法传至欧洲.1874年，英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”，“中国剩余定理”讲的是一个关于整除的问题，现有这样一个整除问题：将1至2022这2022个数中，能被5除余1且被7除余1的数按由小到大的顺序排成一列，构成数列{an}，则此数列的项数为（ ）
A．58B．57C．56D．55
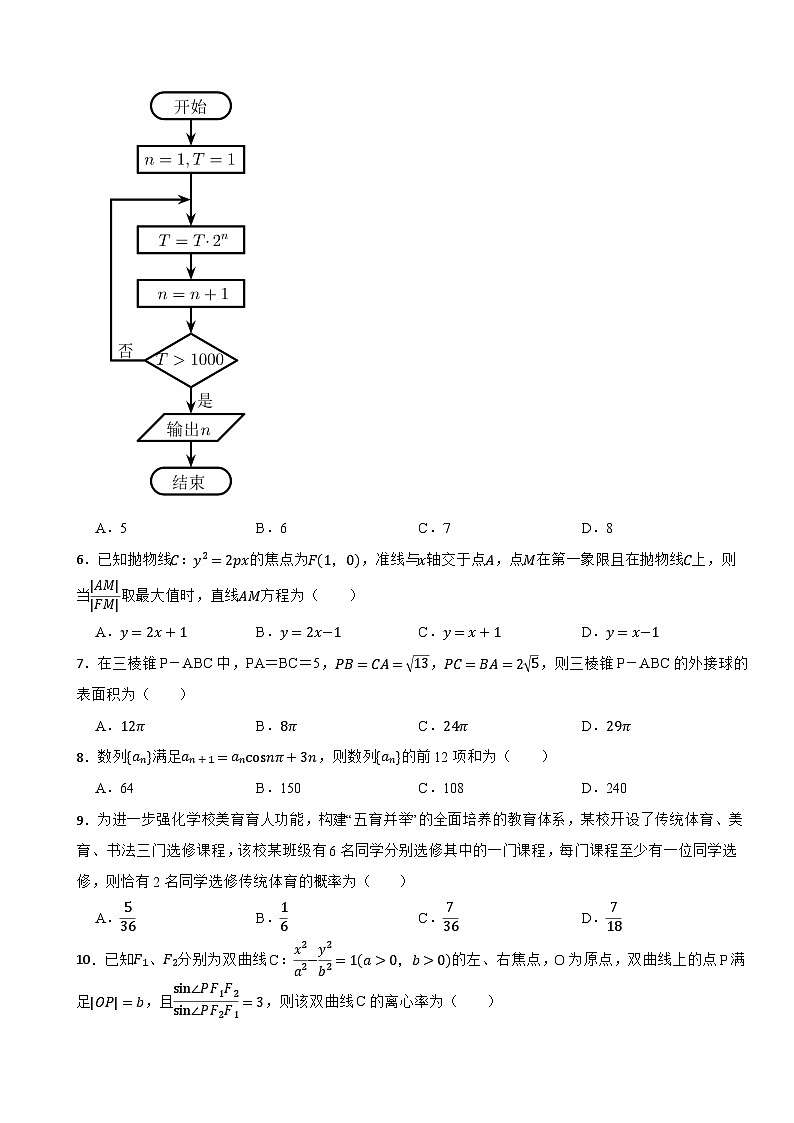
5．已知一个程序框图如图，则输出的n的值等于（ ）
A．5B．6C．7D．8
6．已知抛物线C：y2=2px的焦点为F(1，0)，准线与x轴交于点A，点M在第一象限且在抛物线C上，则当|AM||FM|取最大值时，直线AM方程为（ ）
A．y=2x+1B．y=2x−1C．y=x+1D．y=x−1
7．在三棱锥P－ABC中，PA＝BC＝5，PB=CA=13，PC=BA=25，则三棱锥P－ABC的外接球的表面积为（ ）
A．12πB．8πC．24πD．29π
8．数列{an}满足an+1=ancsnπ+3n，则数列{an}的前12项和为（ ）
A．64B．150C．108D．240
9．为进一步强化学校美育育人功能，构建“五育并举”的全面培养的教育体系，某校开设了传统体育、美育、书法三门选修课程，该校某班级有6名同学分别选修其中的一门课程，每门课程至少有一位同学选修，则恰有2名同学选修传统体育的概率为（ ）
A．536B．16C．736D．718
10．已知F1、F2分别为双曲线C：x2a2−y2b2=1(a>0，b>0)的左、右焦点，O为原点，双曲线上的点P满足|OP|=b，且sin∠PF1F2sin∠PF2F1=3，则该双曲线C的离心率为（ ）
A．2B．62C．2D．3
11．已知f(x)=2x2+3x+1，x≤0|lg2x|，x>0，函数g(x)=f(x)+b有四个不同的零点x1，x2，x3，x4，且满足：x11000，n＝5，满足T>1000，跳出循环，n＝5。
故答案为：A.
【分析】利用已知条件结合程序框图的顺序结构、条件结构和循环结构，进而得出输出的n的值。
6．【答案】C
【知识点】直线与圆锥曲线的综合问题
【解析】【解答】过点M作MM1与准线垂直，垂足为M1，|AM||FM|=|AM||MM1|=1cs∠AMM1=1cs∠MAF，如图：
当|AM||FM|最大时，∠MAF取最大值，此时AM与抛物线相切，
∵抛物线的焦点F(1，0)，∴y2=4x，
设切线方程为y=k(x+1)，则y=k(x+1)y2=4x，∴k2x2+(2k2−4)x+k2=0，
由k2≠0Δ=(2k2−4)2−4k4=0解得k2=1，k=±1，
∵点M在第一象限内，∴k=1，直线方程为：y=x+1。
故答案为：C.
【分析】过点M作MM1与准线垂直，垂足为M1，再利用余弦函数的定义得出|AM||FM|=|AM||MM1|=1cs∠MAF，当|AM||FM|最大时，∠MAF取最大值，此时AM与抛物线相切，再利用抛物线的焦点F(1，0)，从而得出p的值，进而得出抛物线的标准方程，设切线方程的点斜式方程为y=k(x+1)，再利用直线与抛物线相交，联立二者方程结合判别式法得出k2≠0Δ=(2k2−4)2−4k4=0，进而得出k的值，再利用点M在第一象限内，从而求出满足要求的k的值，进而得出直线 AM的方程。
7．【答案】D
【知识点】球的体积和表面积
【解析】【解答】三棱锥P－ABC中，PA＝BC＝5，PB=CA=13，PC=AB=25，
构造长方体使得面对角线分别为5，25，13，则长方体体对角线长等于三棱锥外接球直径2R，如图所示，
设长方体棱长分别为a，b，c，则b2+c2=20，a2+b2=25，a2+c2=13，
则a2+b2+c2=29，即4R2=29，外接球表面积4πR2=29π。
故答案为：D
【分析】在三棱锥P－ABC中，PA＝BC＝5，PB=CA=13，PC=AB=25，构造长方体使得面对角线分别为5，25，13，再利用长方体体对角线长等于三棱锥外接球直径2R，设长方体棱长分别为a，b，c，再结合勾股定理得出球的半径长，再利用球的表面积公式得出三棱锥P－ABC的外接球的表面积。
8．【答案】C
【知识点】函数的周期性；数列的求和
【解析】【解答】利用a1=a1，再分别代入n=1，2，3可得a2=−a1+3，a3=a2+6=−a1+9，a4=−a3+9=a1，a1+a2+a3+a4=12.
由csnπ周期为2，同理可得a5+a6+a7+a8=36，a9+a10+a11+a12=60，
∴S12=12+36+60=108。
故答案为：C.
【分析】利用已知条件结合数列的递推公式和函数的周期性，进而结合求和法得出数列{an}的前12项和 。
9．【答案】D
【知识点】古典概型及其概率计算公式；简单计数与排列组合
【解析】【解答】6名同学分别选修一门课程，每门课程至少有一位同学选修，共有(C62C42C22A33+C64+C61C52C33).A33=540种，
恰有2名同学选修传统体育的情况：C62⋅(C41+C42C22A22)⋅A22=210种，
∴P=210540=718。
故答案为：D
【分析】利用已知条件结合组合数公式和排列数公式解决计数问题的方法，再结合古典概型求概率公式，进而得出恰有2名同学选修传统体育的概率。
10．【答案】D
【知识点】双曲线的简单性质；正弦定理；余弦定理
【解析】【解答】因为F1，F2分别为双曲线的左右焦点，
由正弦定理得到|PF2|sin∠PF1F2=|PF1|sin∠PF2F1，
又因为sin∠PF1F2sin∠PF2F1=3得|PF2||PF1|=3，
又∵||PF2|−|PF1||=2a，
∴|PF1|=a，|PF2|=3a，
在△OPF1中，|OF1|=c，|PF1|=a，|OP|=b，
∴∠OPF1=90°，cs∠PF1O=|PF1||OF1|=ac，
在△PF1F2中，cs∠PF1O=a2+4c2−9a22⋅a⋅2c=a2+4c2−9a24ac，
所以a2+4c2−9a24ac=ac，
化简得e=ca=3。
故答案为：D.
【分析】利用F1，F2分别为双曲线的左右焦点，由正弦定理结合sin∠PF1F2sin∠PF2F1=3得|PF2||PF1|的值，再利用双曲线的定义得出|PF1|=a，|PF2|=3a，在△OPF1中，|OF1|=c，|PF1|=a，|OP|=b，再结合双曲线中a，b，c三者的关系式得出∠OPF1=90°，再利用余弦函数的定义得出|PF1||OF1|=ac，在△PF1F2中结合余弦定理得出a，c的关系式，再结合双曲线的离心率公式变形得出双曲线的离心率。
11．【答案】A
【知识点】函数的零点与方程根的关系
【解析】【解答】如图，作出f(x)图象，若y＝－b与y=f(x)有四个交点，需00)，再利用求导的方法判断函数的单调性，进而得出函数的最大值，从而得出b的最大值。
17．【答案】（1）解：由正弦定理asinA=bsinB=csinC=2R，可得RsinC=12c，a=2RsinA，b=2RsinB，
∴csC(acsB+bcsA)=2RcsC(sinAcsB+sinBcsA)=2RcsCsin(A+B)=2RcsCsinC=ccsC，
所以ccsC=12c，则csC=12，
因为00得m∈R，
设M(x1，y1)，N(x2，y2)，则y1+y2=−2mm2+9，y1y2=−8m2+9（*），
kTM⋅kTN=y1x1−t⋅y2x2−t=y1my1+1−t⋅y2my2+1−t=y1y2m2y1y2+m(1−t)(y1+y2)+(1−t)2，
将（*）代入上式，可得：−8m2+9m2⋅−8m2+9+m(1−t)(−2mm2+9)+(1−t)2=8(9−t2)m2−9(1−t)2，
要使kTM⋅kTN为定值，则有9−t2=0，又∵t>0，∴t＝3，
此时kTM⋅kTN=8−9×4=−29，
∴存在点T(3，0)，使得直线TM与TN斜率之积为定值−29，此时t＝3.
【知识点】椭圆的标准方程；直线与圆锥曲线的综合问题
【解析】【分析】（1）利用已知条件结合长轴和短轴的定义，进而得出a，b的关系式，再利用代入法和椭圆中a，b，c三者的关系式，进而得出a，b，c的值，从而得出椭圆的标准方程。
（2）由已知知直线l过Q(1，0)，设l的方程为x＝my＋1，再利用直线与椭圆相交，联立二者方程结合判别式法得出m的取值范围，设M(x1，y1)，N(x2，y2)，再利用韦达定理得出y1+y2=−2mm2+9，y1y2=−8m2+9（*），再利用两点求斜率公式得出
kTM⋅kTN=y1y2m2y1y2+m(1−t)(y1+y2)+(1−t)2，将（*）代入上式，可得：−8m2+9m2⋅−8m2+9+m(1−t)(−2mm2+9)+(1−t)2=8(9−t2)m2−9(1−t)2，要使kTM⋅kTN为定值，则有9−t2=0，再利用t>0得出t的值，进而得出此时kTM⋅kTN的值，所以存在点T(3，0)，使得直线TM与TN斜率之积为定值−29，此时t＝3。
21．【答案】（1）解：f(x)定义域为(0，+∞)，由于f(x)=lnx−kx有一个零点，可得方程k=lnxx有且仅有一个实根，
令ℎ(x)=lnxx，ℎ′(x)=1−lnxx2，由ℎ′(x)>0得00)，μ′(x)=−exx−1x0；x∈(1，+∞)，μ(x)0，x∈(1，+∞)，φ′(x)0，∴ex−lnx+kx≥ex−lnx+(1−e)x=ex−ex+(x−lnx)（*），
现证明，ex≥ex，x−lnx≥1，构造A(x)=ex−ex，A′(x)=ex−e，
令A′(x)0得出ex−lnx+kx≥ex−ex+(x−lnx)（*），现证明，ex≥ex，x−lnx≥1，构造A(x)=ex−ex，再利用求导的方法判断函数的单调性，进而得出函数的最小值，所以A(x)≥A(1)=0成立；构造B(x)=x−lnx，再利用求导的方法判断函数的单调性，进而得出函数的最小值，所以B(x)≥B(1)=1成立，所以（*）式≥1成立，原式得证。
22．【答案】（1）解：由于x=2−3ty=t，消t得2−3y=x，即x+3y−2=0，
由ρ⋅sin2θ=6csθ得ρ2⋅sin2θ=6ρcsθ，∴曲线C的直角坐标方程是：y2=6x.
（2）解：将直线l：x=2−3ty=t化为标准形式x=2−32t′y=12t′，
代入y2=6x，(12t′)2=6(2−32t′)并化简得t′2+123t′−48=0.
Δ=624>0，设A，B对应参数为t1，t2，t1t2=−48，所以|AM|⋅|BM|=|t1t2|=48.
【知识点】平面内两点间的距离公式；点的极坐标和直角坐标的互化；参数方程化成普通方程
【解析】【分析】（1）利用已知条件结合参数方程与普通方程的转化方法，再结合极坐标和直角坐标的互化公式，进而得出直线l普通方程与曲线C的直角坐标方程。
（2）利用已知条件，由点斜式方程设出直线l方程，再结合直线l与曲线C相交，联立二者方程求出交点A，B的坐标，再结合已知条件 M(2，0)和两点距离公式得出 |AM|⋅|BM|的值。
23．【答案】（1）解：由于f(x)=|x−2|+|x+1|=−2x+1，x≤−13，−1