河南省六市TOP二十名校2022-2023学年高三上学期理数9月摸底考试试卷（文字版，含解析）

这是一份河南省六市TOP二十名校2022-2023学年高三上学期理数9月摸底考试试卷（文字版，含解析），共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题（共12小题，每小题5分，共60分）
1．设集合A={x|x≥2}，B={1，2，4，5}，则B∩∁RA=（ ）
A．{1}B．{1，2}C．{1，2，4}D．{4，5}
2．已知复数z满足(z−i)(z+i)=1，则|z−i|=（ ）
A．1B．2C．5D．22
3．已知向量a，b满足|a|=|b|=1，(2a−b)⊥b，则a与b的夹角为（ ）
A．π6B．π3C．π2D．2π3
4．中国公民身份号码编排规定，女性公民的顺序码为偶数，男性为奇数，反映了性别与数字之间的联系；数字简谱以1，2，3，4，5，6，7代表音阶中的7个基本音阶，反映了音乐与数字之间的联系，同样我们可以对几何图形赋予新的含义，使几何图形与数字之间建立联系.如图1，我们规定1个正方形对应1个三角形和1个正方形，1个三角形对应1个正方形，在图2中，第1行有1个正方形和1个三角形，第2行有2个正方形和1个三角形，则在第9行中的正方形的个数为（ ）
A．53B．55C．57D．59
5．已知抛物线C：y2=4x的焦点为F，准线为l，与x轴平行的直线与l和C分别交于A，B两点，且若|AF|=|BF|，则|AB|=（ ）
A．2B．22C．23D．4
6．已知等比数列{an}的公比q>0，前n项和为Sn，3a1−S3=60，a2−a4=18，则a5=（ ）
A．2B．3C．6D．10
7．在正方体ABCD−A1B1C1D1中，P，Q分别为AB，CD的中点，则（ ）
A．AB1∥平面BC1QB．平面AB1D1∥平面BC1Q
C．A1Q⊥平面B1DPD．平面B1CD⊥平面B1DP
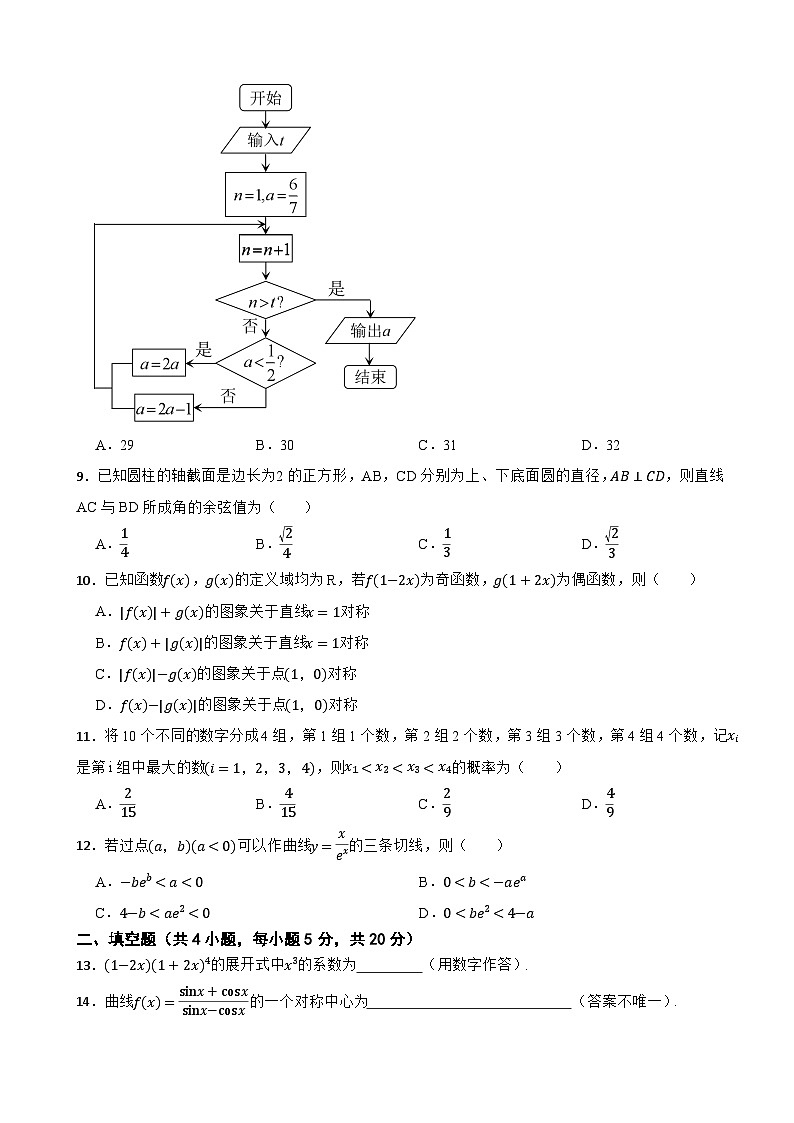
8．执行如图所示的程序框图，输出的a的值为37，则输入的t的值可以为（ ）
A．29B．30C．31D．32
9．已知圆柱的轴截面是边长为2的正方形，AB，CD分别为上、下底面圆的直径，AB⊥CD，则直线AC与BD所成角的余弦值为（ ）
A．14B．24C．13D．23
10．已知函数f(x)，g(x)的定义域均为R，若f(1−2x)为奇函数，g(1+2x)为偶函数，则（ ）
A．|f(x)|+g(x)的图象关于直线x=1对称
B．f(x)+|g(x)|的图象关于直线x=1对称
C．|f(x)|−g(x)的图象关于点(1，0)对称
D．f(x)−|g(x)|的图象关于点(1，0)对称
11．将10个不同的数字分成4组，第1组1个数，第2组2个数，第3组3个数，第4组4个数，记xi是第i组中最大的数(i=1，2，3，4)，则x1A．215B．415C．29D．49
12．若过点(a，b)(a<0)可以作曲线y=xex的三条切线，则（ ）
A．−bebC．4−b二、填空题（共4小题，每小题5分，共20分）
13．(1−2x)(1+2x)4的展开式中x3的系数为 （用数字作答）.
14．曲线f(x)=sinx+csxsinx−csx的一个对称中心为 （答案不唯一）.
15．已知双曲线C：x2a2−y2b2=1(a>0，b>0)的右焦点为F，P为C右支上一点，⊙P与x轴切于点F，与y轴交于A，B两点，若△APB为直角三角形，则C的离心率为 .
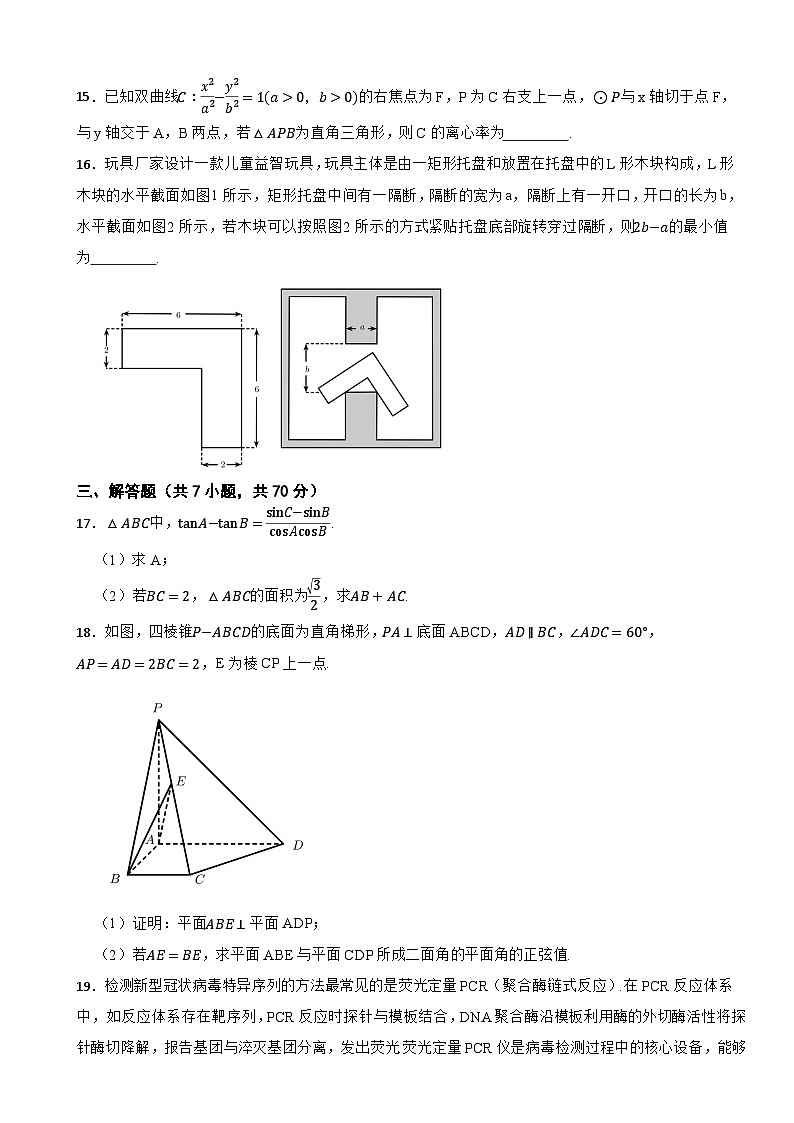
16．玩具厂家设计一款儿童益智玩具，玩具主体是由一矩形托盘和放置在托盘中的L形木块构成，L形木块的水平截面如图1所示，矩形托盘中间有一隔断，隔断的宽为a，隔断上有一开口，开口的长为b，水平截面如图2所示，若木块可以按照图2所示的方式紧贴托盘底部旋转穿过隔断，则2b−a的最小值为 .
三、解答题（共7小题，共70分）
17．△ABC中，tanA−tanB=sinC−sinBcsAcsB.
（1）求A；
（2）若BC=2，△ABC的面积为32，求AB+AC.
18．如图，四棱锥P−ABCD的底面为直角梯形，PA⊥底面ABCD，AD∥BC，∠ADC=60°，AP=AD=2BC=2，E为棱CP上一点.
（1）证明：平面ABE⊥平面ADP；
（2）若AE=BE，求平面ABE与平面CDP所成二面角的平面角的正弦值.
19．检测新型冠状病毒特异序列的方法最常见的是荧光定量PCR（聚合酶链式反应）.在PCR反应体系中，如反应体系存在靶序列，PCR反应时探针与模板结合，DNA聚合酶沿模板利用酶的外切酶活性将探针酶切降解，报告基团与淬灭基团分离，发出荧光.荧光定量PCR仪是病毒检测过程中的核心设备，能够监测出荧光到达预先设定阈值的循环数（Ct值）与病毒核酸浓度有关，病毒核酸浓度越高，Ct值越小.某第三方核酸检测机构先后采用过甲、乙两家公司的荧光定量PCR仪，日核酸检测量分别为600管和1000管，现两家公司分别推出升级方案，受各种因素影响，升级后核酸检测量变化情况与相应概率p如下表所示：
甲公司：
乙公司：
（1）求至少有一家公司的升级方案使得日核酸检测量增加不低于50％的概率；
（2）以日核酸检测量为依据，该检测机构应选哪家公司的仪器？
20．已知椭圆C：x2a2+y2b2=1(a>b>0)的左、右顶点分别为A，B，左焦点为F，|AF|=1，|BF|=3.
（1）求C的方程；
（2）设M，N是C上在x轴两侧的两点，直线AM与BN交于点P，若P的横坐标为4，求△FMN的周长.
21．已知函数f(x)=x(x−lnx−1).
（1）讨论f(x)的零点个数；
（2）若af(x)≤ex−1−x，求a的取值范围.
22．在直角坐标系xOy中，直线l的参数方程为x=2+12ty=32t（t为参数）.以坐标原点为极点，x轴非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρ=msinθtanθ(m>0).
（1）写出C的直角坐标方程；
（2）l与C交于A，B两点，与x轴交于点P，若|PA|=2|PB|，求m.
23．已知a，b都是正数，且a+b=2，证明：
（1）a+b≥2；
（2）1a2+1++1b2+1≥1.
答案解析部分
1．【答案】B
【知识点】交集及其运算；补集及其运算
【解析】【解答】A={x|x≥4}，∁RA={x|x<4}，则B∩∁RA={1，2}.
故答案为：B
【分析】 解不等式求得集合A，根据集合的基本运算求得∁RA，进而求得 B∩∁RA的值 .
2．【答案】A
【知识点】复数代数形式的乘除运算；复数的模
【解析】【解答】设z=x+yi(x，y∈R)，则z=x−yi，
(z−i)(z+i)=(x+(y−1)i)(x−(y−1)i)=x2+(y−1)2=1，
|z−i|=x2+(y−1)2=1，
故答案为：A.
【分析】 结合复数的四则运算进行化简，然后结合复数的模长公式可求出答案.
3．【答案】B
【知识点】数量积表示两个向量的夹角
【解析】【解答】由(2a−b)⊥b可得(2a−b)⋅b=2a⋅b−b2=0，
则2|a|⋅|b|cs⟨a，b⟩−|b|2=0，
又|a|=|b|=1，则cs⟨a，b⟩=12，
所以a与b的夹角为π3.
故答案为：B.
【分析】 由已知可求得(2a−b)⋅b=2a⋅b−b2=0，再由夹角公式求解，即可求出a与b的夹角.
4．【答案】B
【知识点】数列的递推公式
【解析】【解答】设an为第n行中正方形的个数，bn为第n行中三角形的个数，由于每个正方形产生下一行的1个三角形和1个正方形，
每个三角形产生下一行的1个正方形，则有an+1=an+bn，bn+1=an，
整理得an+1=an+an−1(n≥2)，且a1=1，a2=2，
则a3=a2+a1=3，a4=a3+a2=5，a5=a4+a3=8，a6=a5+a4=13，
a7=a6+a5=21，a8=a7+a6=34，a9=a8+a7=55.
故答案为：B.
【分析】设an为第n行中正方形的个数，bn为第n行中三角形的个数，再推断与下一行的关系，从而得出第9行的个数.
5．【答案】D
【知识点】抛物线的定义
【解析】【解答】由抛物线的定义可知|AF|=|BF|=|AB|，△ABF为等边三角形，
设准线l与x轴交于点H，则|FH|=2，
∠HAF=30°，所以|AB|=|AF|=2|FH|=4.
故答案为：D
【分析】 由抛物线的定义可知△ABF为正三角形，然后求解出答案.
6．【答案】B
【知识点】等比数列的通项公式
【解析】【解答】设等比数列{an}的首项为a1，公比为q，
由题意可得2a1−a2−a3=60a2−a4=18，即a1(2−q−q2)=60a1q(1−q2)=18，
整理得a1(1−q)(2+q)=60a1q(1−q)(1+q)=18，解得q=12或q=−65（舍去），a1=48，
所以a5=a1q4=3.
故答案为：B.
【分析】 由已知结合等比数列的求和公式及通项公式可求出首项及公比，进而可求出答案.
7．【答案】D
【知识点】直线与平面平行的判定；平面与平面平行的判定；直线与平面垂直的判定；平面与平面垂直的判定
【解析】【解答】如图，因为AB1∥C1D，而C1D与平面BC1Q相交，则A选项不正确；
因为DP∥BQ，B1P∥C1Q，所以平面B1DP∥平面BC1Q，
而平面AB1D1与平面B1DP相交，则B选项不正确；
在矩形A1B1CD中，A1Q与B1D不垂直，即A1Q与平面B1DP不垂直，则C选项不正确；
设B1D的中点为G，因为DP=B1P，所以GP⊥B1D，
又因为GP∥BC1，BC1⊥B1C，所以GP⊥B1C，
所以GP⊥平面B1CD，所以平面B1CD⊥平面B1DP，则D选项正确.
故答案为：D.
【分析】由线面的位置关系可判断A；由面面平行的判定和性质可判断B；由线面垂直的判定和性质可判断C；建立空间直角坐标系，由法向量的关系可判断D.
8．【答案】B
【知识点】循环结构
【解析】【解答】程序运行如下：n=1，a=67；n=2，a=57；n=3，a=37；n=4，a=67；…，
此程序的a值3个一循环.若输出的a的值为37，则输入的t的值为3k(k∈N∗)，仅有B符合；
故答案为：B.
【分析】 先运行程序框图，找出规律即可得到答案.
9．【答案】C
【知识点】余弦定理
【解析】【解答】如图，作正四棱柱AEBF−GCHD，
使棱柱的顶点分别在圆柱的上、下底面圆上，AC∩EG=O.
由题意可知，AB=AG=2，AE=2，OA=OE=62.
由EG∥BD可知，∠AOE即为直线AC与BD所成的角或其补角，
所以cs∠AOE=OA2+OE2−AE22OA⋅OE=(62)2+(62)2−(2)22×62×62=13.
故答案为：C.
【分析】 作正四棱柱AEBF−GCHD，使棱柱的顶点分别在圆柱的上、下底面圆上，AC∩EG=O，由EG∥BD可知，∠AOE即为直线AC与BD所成的角或其补角，利用余弦定理计算出异面直线AC与BD所成角的余弦值.
10．【答案】A
【知识点】奇函数与偶函数的性质；奇偶函数图象的对称性
【解析】【解答】因为f(1−2x)为奇函数，所以f(1+2x)=−f(1−2x)，
所以函数f(x)的图象关于点(1，0)对称，则|f(x)|的图象关于直线x=1对称.
因为g(1+2x)为偶函数，所以g(1−2x)=g(1+2x)，
所以函数g(x)的图象关于直线x=1对称，
所以|f(x)|+g(x)的图象关于直线x=1对称.
故答案为：A.
【分析】 由f(1−2x)为奇函数得f(1+2x)=−f(1−2x)，从而|f(x)|的图象关于直线x=1对称，由g(1+2x)为偶函数，得函数g (x)的图象关于直线x=1对称，由此推导出|f(x)|+g(x)的图象关于直线x=1对称.
11．【答案】A
【知识点】相互独立事件的概率乘法公式
【解析】【解答】最大的数在第4组的概率P4=410=25，
在前3组中，最大的数在第3组的概率P3=36=12，
在前2组中，最大的数在第2组的概率P2=23，
x1故答案为：A.
【分析】 先考虑10个数中最大数必然在第四组，求出概率，再顺次考虑剩余6个数的最大数必然在第三组，求出概率，以此类推下去，可得答案.
12．【答案】D
【知识点】利用导数研究函数的单调性
【解析】【解答】y′=1−xex，设切点为(x0，x0ex0)，则1−x0ex0=x0ex0−bx0−a，整理得x02−ax0+aex0=b，
由题意知关于x0的方程x02−ax0+aex0=b有三个不同的解.
设f(x)=x2−ax+aex，f′(x)=−(x−a)(x−2)ex，
由f′(x)=0得x=a或x=2，
又a<0，所以当x当a0，f(x)单调递增，
当x>2时，f′(x)<0，f(x)单调递减.
又易知y=x2−ax+a在(−∞，a2)上单调递减，在(a2，+∞)上单调递增，开口向上，
所以当x趋向于负无穷或正无穷时，y=x2−ax+a都趋向于正无穷.
而当x趋向于负无穷时，y=(1e)x趋向于正无穷，故f(x)=x2−ax+aex=(x2−ax+a)(1e)x也就趋向于正无穷；
当x趋向于正无穷时，y=ex趋向于正无穷且增长速率远远超过y=x2−ax+a，故f(x)=x2−ax+aex>0且趋向于零，
又f(a)=aea<0，f(2)=4−ae2>0，函数f(x)的大致图像如图所示.
因为f(x)的图像与直线y=b有三个交点，
所以0故答案为：D.
【分析】 设切点为(x0，x0ex0) ，利用导数求出过切点的切线方程，问题转化为方程x02−ax0+aex0=b有三个不同的解，设f(x)=x2−ax+aex，利用导数研究其单调性与最值，画出函数f (x)的大致图象，数形结合得答案.
13．【答案】-16
【知识点】二项式定理
【解析】【解答】由于(1+2x)4展开式的通项公式为Tr+1=C4r(2x)r，
当r=2时，x2的系数为C42×22=24；
当r=3时，x3的系数为C43×23=32；
(1−2x)(1+2x)4的展开式中含x3的系数为−2×24+1×32=−16.
故答案为：-16.
【分析】 根据已知，只要求出(1+2x)4展开式中的含x2，x3的系数即可求解出展开式中x3的系数 .
14．【答案】(π4，0)（答案不唯一）
【知识点】两角和与差的正切公式；正切函数的图象与性质；同角三角函数间的基本关系
【解析】【解答】f(x)=sinx+csxsinx−csx=tanx+1tanx−1=−tanx+tanπ41−tanxtanπ4=−tan(x+π4)，
令x+π4=k1π或x+π4=π2+k2π(k1，k2∈Z)，
则x=−π4+k1π或x=π4+k2π，
令k2=0，则x=π4.所以函数的一个对称中心是(π4，0).
故答案为：(π4，0)（答案不唯一）.
【分析】 根据题意得定义域为f(x)=sinx+csxsinx−csx=−tanx+tanπ41−tanxtanπ4=−tan(x+π4)，根据正切函数的图象与性质，可求出答案.
15．【答案】2+62
【知识点】双曲线的简单性质
【解析】【解答】不妨设点P在x轴的上方，由题意可知PF⊥x轴，
所以P点的横坐标xP=c，代入x2a2−y2b2=1，得yP=b2a=|PF|.
又△APB为直角三角形，易知∠APB=90°，且|PA|=|PB|=|PF|，
则有|PF|=2c，即b2a=2c，
则2ac=c2−a2，即(ca)2−2⋅ca−1=0，则e=ca=2+62.
故答案为：2+62
【分析】 设点P在x轴的上方，由题意可知PF⊥x轴，又△APB为直角三角形，易知∠APB=90°，且|PA|=|PB|=|PF|，再结合b2=c2-a2及e=ca，求解出 C的离心率 .
16．【答案】42
【知识点】三角函数中的恒等变换应用
【解析】【解答】解法1：如图，作HF⊥AB于F，DG⊥AB于G，延长CD交AB于E，
设∠AED=θ，点A到直线CD的距离为h.
由题意可知，AF=DG=2，CD=a，
则ℎ=AE⋅sinθ=(AF+FG+GE)⋅sinθ
=(AF+CD⋅csθ+DGtanθ)⋅sinθ=(2+acsθ+2tanθ)sinθ
=2sinθ+asinθcsθ+2csθ=22sin(θ+π4)+a2sin2θ.
当θ=π4时，h取最大值22+a2.
若木块可以旋转穿过隔断，则有22+a2≤b，
即2b−a≥42，故2b−a的最小值为42.
解法2：如图，设CD的中点为I，点A到直线CD的距离为h，
由题意可知AH=22，由∠CHD=π2，可知HI=12CD=a2.
则有ℎ≤AI≤AH+HI，
当AH⊥CD时，两个等号同时成立，此时h取最大值AH+HI=22+a2.
若木块可以旋转穿过隔断，则有22+a2≤b，即2b−a≥42，
故2b−a的最小值为42.
故答案为：42
【分析】 作HF⊥AB于F，DG⊥AB于G，延长CD交AB于E，设∠AED=θ，可得ℎ=22sin(θ+π4)+a2sin2θ，可得22+a2≤b，可求出2b−a的最小值.
17．【答案】（1）解：由tanA−tanB=sinC−sinBcsAcsB，
可得sinAcsA−sinBcsB=sinC−sinBcsAcsB，
整理得sinAcsB−csAsinB=sinC−sinB.
则sinAcsB−csAsinB=sin(A+B)−sinB，
即sinAcsB−csAsinB=sinAcsB+csAsinB−sinB，
故sinB=2csAsinB.
由sinB≠0，故csA=12，
又A∈(0，π)，所以A=π3.
（2）解：设△ABC的内角A，B，C所对的边分别为a，b，c，
因为A=π3，所以△ABC的面积S=12bcsinA=34bc=32，
所以bc=2.
因为BC=a=2，由余弦定理a2=b2+c2−2bccsA，
得b2+c2−bc=(b+c)2−3bc=4，
所以AB+AC=b+c=10.
【知识点】两角和与差的正弦公式；余弦定理
【解析】【分析】 (1)根据同角三角函数关系和两角差公式将已知条件进行变形可得csA的值，结合A的取值范围可得A角的值；
(2)由三角形面积公式可得bc的值，再利用余弦定理可求得 AB+AC的值.
18．【答案】（1）证明：由题意可知AB⊥AD，
因为PA⊥底面ABCD，AB⊂平面ABCD，所以AB⊥AP，
又AP∩AD=A，所以AB⊥平面ADP，
又AB⊂平面ABE，所以平面ABE⊥平面ADP.
（2）解：由题意可知△ACD为等边三角形，且AB=3.
连接AC，作EF⊥AC于F，连接BF，
则有EF∥AP，且EF⊥平面ABCD，
因为AE=BE，所以AF=BF，
所以AF=CF，故E为CP的中点.
以A为坐标原点，AB，AD，AP的方向分别为x轴、y轴、z轴的正方向建立如图所示的空间直角坐标系，
则A(0，0，0)，B(3，0，0)，C(3，1，0)，D(0，2，0)，E(32，12，1)，P(0，0，2).
设平面ABE的一个法向量n1=(x1，y1，z1)，
AB=(3，0，0)，AE=(32，12，1)，
则AB⋅n1=0AE⋅n1=0，即3x1=032x1+12y1+z1=0，可取n1=(0，2，−1).
设平面CDP的一个法向量n2=(x2，y2，z2)，PC=(3，1，−2)，PD=(0，2，−2)，
则PC⋅n2=0PD⋅n2=0，即3x2+y2−2z2=02y2−2z2=0，可取n2=(1，3，3).
则cs⟨n1，n2⟩=23−35×7=10535，
即所求角的正弦值为1−(10535)2=47035.
故平面ABE与平面CDP所成二面角的平面角的正弦值为47035.
【知识点】平面与平面垂直的判定；用空间向量研究二面角
【解析】【分析】(1)推导出AB⊥AD， AB⊥AP，从而 AB⊥平面ADP， 由此能证明平面ABE⊥平面ADP；
(2)连接AC，作EF⊥AC于E，连接BF，则有EF// AP且EF⊥平面ABCD， 以A为坐标原点，AB，AD，AP的方向分别为x轴、y轴、z轴的正方向建立如图所示的空间直角坐标系， 利用向量法能求出平面ABE与平面CDP所成二面角的平面角的正弦值.
19．【答案】（1）解：记事件A为“甲公司的方案使日核酸检测量增加不低于50％”，
事件B为“乙公司的方案使日核酸检测量增加不低于50％”，
事件C为“至少有一家公司的升级方案使得日核酸检测量增加不低于50％”
则C=AB∪AB∪AB，且A，B相互独立.
由题意可知P(A)=34+112=56，P(B)=12+14=34.
P(C)=P(AB)+P(AB)+P(AB)=56×(1−34)+(1−56)×34+56×34=2324，
故至少有一家公司的升级方案使得日核酸检测量增加不低于50％的概率为2324.
（2）解：设采用甲公司的仪器和改造方案后日核酸检测量为X，采用乙公司的仪器和改造方案后日核酸检测量为Y，
随机变量X的分布列为：
则E(X)=1800×34+900×112+540×16=1515.
随机变量Y的分布列为：
则E(Y)=1800×12+1500×14+1100×14=1550.
故E(X)【知识点】相互独立事件的概率乘法公式；离散型随机变量及其分布列；离散型随机变量的期望与方差
【解析】【分析】(1)由题意结合事件的独立性求解至少有一家公司的升级方案使得日核酸检测量增加不低于50%的概率即可；
(2)分别求得两家公司的数学期望，然后给出结论即可.
20．【答案】（1）解：设椭圆C的半焦距为c，
由|AF|=1，|BF|=3，可得a−c=1，a+c=3.
则a=2，c=1，b2=a2−c2=3，
所以椭圆C的方程为x24+y23=1
（2）解：由C的方程可知A(−2，0)，B(2，0)，设P(4，t)，M(x1，y1)，N(x2，y2)，
则直线AM的方程为y=t6(x+2)，直线BN的方程为y=t2(x−2)，
由y=t6(x+2)x24+y23=1，得(27+t2)x2+4t2x+4t2−108=0，
Δ=16t4−4(27+t2)(4t2−108)>0，
所以(−2)⋅x1=4t2−10827+t2，则x1=54−2t227+t2.
所以M(54−2t227+t2，18t27+t2)，
由y=t2(x−2)x24+y23=1，得(3+t2)x2−4t2x+4t2−12=0，
Δ=16t4−4(3+t2)(4t2−12)>0
所以2x2=4t2−123+t2，得x2=2t2−63+t2
所以N(2t2−63+t2，−6t3+t2).
所以直线MN的斜率为18t27+t2+6t3+t254−2t227+t2−2t2−63+t2=18t(3+t2)+6t(27+t2)(54−2t2)(3+t2)−(2t2−6)(27+t2)=−6tt2−9
所以直线MN的方程为y+6t3+t2=−6tt2−9(x−2t2−63+t2)，
即y=−6tt2−9x+6tt2−9=−6tt2−9(x−1)，
故直线MN恒过右焦点F′(1，0).
则有△FMN的周长L=|MF|+|NF|+|MN|=|MF|+|MF′|+|NF|+|NF′|=4a=8，
所以△FMN的周长为8.
【知识点】椭圆的标准方程；直线与圆锥曲线的综合问题
【解析】【分析】(1)由已知可得 a−c=1，a+c=3，可求出C的方程；
(2) 设P(4，t)，M(x1，y1)，N(x2，y2)， 与椭圆联立方程组，可得 x2=2t2−63+t2 ，求出 直线MN的方程，进而求出直线MN恒过右焦点F′(1，0)，可求出△FMN的周长.
21．【答案】（1）解：设F(x)=x−lnx−1，
∵F(x)的定义域为(0，+∞)，可知f(x)与F(x)的零点相同.
F′(x)=1−1x=x−1x，当x∈(0，1)时，F′(x)<0，F(x)单调递减，
当x∈(1，+∞)时，F′(x)>0，F(x)单调递增，
当x=1时F(x)取得最小值，且F(1)=0，则F(x)有且只有1个零点，
故f(x)有且只有1个零点.
（2）解：方法一：由af(x)≤ex−1−x，得ex−1−x−ax(x−lnx−1)≥0，
由x>0，得ex−1x−1−a(x−lnx−1)≥0，设g(x)=ex−1x−1−a(x−lnx−1)，
则g(1)=0，g′(x)=ex−1(x−1)x2−a⋅x−1x=x−1x2(ex−1−ax).
设G(x)=ex−1−x(x>0)，G′(x)=ex−1−1，
当x∈(0，1)时，G′(x)<0，G(x)单调递减，
当x∈(1，+∞)时，G′(x)>0，G(x)单调递增，则G(x)≥G(1)=0，
当a≤1时，因为x∈(0，+∞)，所以ex−1−ax≥ex−1−x≥0.
所以x∈(0，1)时，g′(x)=x−1x2(ex−1−ax)<0，g(x)单调递减，
x∈(1，+∞)时，g′(x)=x−1x2(ex−1−ax)>0，g(x)单调递增，
故g(x)在(0，+∞)上的最小值为g(1)=0，即af(x)≤ex−1−x恒成立，
当a>1时，设ℎ(x)=ex−1−ax(x>0)，则ℎ(1)=1−a<0，
令ℎ′(x)=ex−1−a=0，得x=1+lna，由a>1知x=1+lna>1.
当x∈(1，1+lna)时，ℎ′(x)<0，ℎ(x)单调递减，∴ℎ(x)<ℎ(1)<0.
故x∈(1，1+lna)时，g′(x)=x−1x2(ex−1−ax)<0，g(x)单调递减，
而g(1)=0，即x∈(1，1+lna)时，g(x)<0，故af(x)≤ex−1−x不成立.
综上，a的取值范围为(−∞，1].
方法二：ax(x−lnx−1)≤ex−1−x
⇔a(x−lnx−1)≤ex−1x−1=ex−lnx−1−1
令t=x−lnx−1，t′=1−1x.
则x∈(0，1)时，t=x−lnx−1递减；x∈(1，+∞)时，t=x−lnx−1递增.
∴t=x−lnx−1≥0.
则af(x)≤ex−1−x⇔at≤et−1对于t≥0恒成立.
令ℎ(t)=et−at−1.则ℎ′(t)=et−a，ℎ′(0)=1−a.
下面分两种情况说明：
若1−a≥0，即a≤1时，ℎ′(t)≥1−a≥0恒成立，ℎ(t)单调递增.
∴ℎ(t)≥ℎ(0)=0符合题意.
若1−a<0，即a>1时，令ℎ′(t)=0，则t=lna.
则t∈(0，lna)时，ℎ(t)递减，ℎ(lna)<ℎ(0)=0，舍去.
综上，a≤1，即a的取值范围为(−∞，1].
【知识点】利用导数研究函数的单调性；利用导数研究函数最大（小）值
【解析】【分析】(1) 设F(x)=x−lnx−1， 由F(x)的定义域可知f (x)与F (x)的零点相同，利用导数研究函数F (x)的单调性可知F (x)有且只有1个零点，从而f (x)仅有一个零点；
(2)将已知条件变形为 ex−1x−1−a(x−lnx−1)≥0， 设g(x)=ex−1x−1−a(x−lnx−1)， 分a≤1和a>1两种情况，利用导数即可求解出 a的取值范围.
22．【答案】（1）解：由ρ=msinθtanθ，整理得ρsin2θ=mcsθ，即ρ2sin2θ=mρcsθ，
又θ≠kπ2(k∈Z)，所以曲线C的直角坐标方程为y2=mx(x≠0).
（2）解：由l的参数方程可知，直线l过点P(2，0)，倾斜角为π3.
把x=2+12ty=32t代入y2=mx，整理得3t2−2mt−8m=0.
设点A，B所对应的参数分别为t1，t2，
由题意可知t1>0，t2<0，
且t1+t2=2m3，①t1t2=−8m3，②
因为|PA|=2|PB|，则有t1=−2t2，③
①③联立，得t1=43m，t2=−23m，
代入②，解得m=3.
【知识点】参数的意义；参数方程化成普通方程
【解析】【分析】 (1)直接利用转换关系，在参数方程极坐标方程和直角坐标方程之间进行转换；
(2)利用一元二次方程根和系数关系式的应用建立方程，进一步求出m的值.
23．【答案】（1）证明：由a+b=2，两边平方整理得2ab=4−(a+b)，
因为a+b≥2ab，当“a=b”时等号成立.
所以a+b≥4−(a+b)，
所以a+b≥2，当“a=b”时，等号成立.
（2）证明：1a2+1+1b2+1−1=b2+1+a2+1−(a2+1)(b2+1)(a2+1)(b2+1)=1−a2b2(a2+1)(b2+1).
由a+b=2，得a+b=4−2ab≥2ab，当“a=b”时等号成立.
则ab≤1，故1−a2b2≥0，所以1−a2b2(a2+1)(b2+1)≥0，
所以1a2+1+1b2+1≥1，当“a=b”时，等号成立.
【知识点】基本不等式
【解析】【分析】 (1)根据基本不等式进行证明即可证得 a+b≥2；
(2)先因式分解，再利用基本不等式进行证明即可.日核酸检测量
增加200％
增加50％
降低10％
p
34
112
16
日核酸检测量
增加80％
增加50％
增加10％
p
12
14
14
X
1800
900
540
p
34
112
16
Y
1800
1500
1100
p
12
14
14