新高考数学一轮复习讲练教案4.5 三角恒等变换（含解析）

这是一份新高考数学一轮复习讲练教案4.5 三角恒等变换（含解析），共20页。

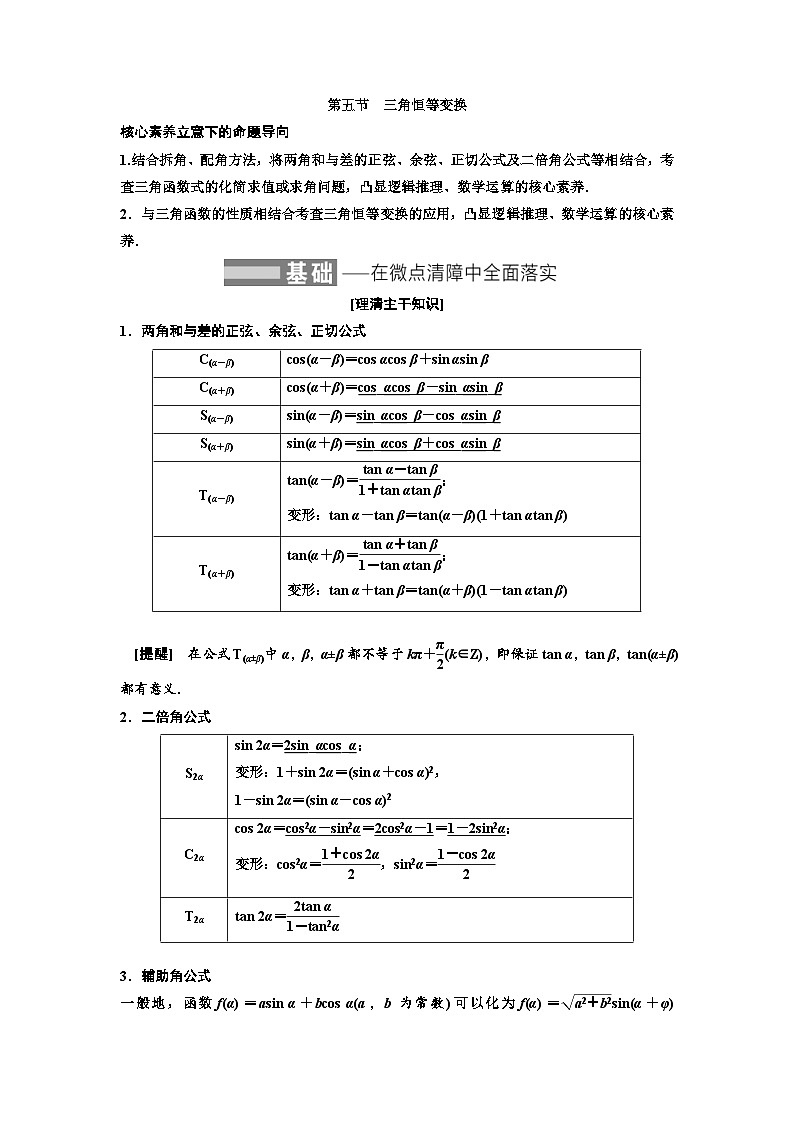
第五节　三角恒等变换
核心素养立意下的命题导向
1.结合拆角、配角方法，将两角和与差的正弦、余弦、正切公式及二倍角公式等相结合，考查三角函数式的化简求值或求角问题，凸显逻辑推理、数学运算的核心素养．
2．与三角函数的性质相结合考查三角恒等变换的应用，凸显逻辑推理、数学运算的核心素养．

[理清主干知识]
1．两角和与差的正弦、余弦、正切公式
C(α－β)
cos(α－β)＝cos αcos β＋sin αsin β
C(α＋β)
cos(α＋β)＝cos_αcos_β－sin_αsin_β
S(α－β)
sin(α－β)＝sin_αcos_β－cos_αsin_β
S(α＋β)
sin(α＋β)＝sin_αcos_β＋cos_αsin_β
T(α－β)
tan(α－β)＝；
变形：tan α－tan β＝tan(α－β)(1＋tan αtan β)
T(α＋β)
tan(α＋β)＝；
变形：tan α＋tan β＝tan(α＋β)(1－tan αtan β)

　[提醒]　在公式T(α±β)中α，β，α±β都不等于kπ＋(k∈Z)，即保证tan α，tan β，tan(α±β)都有意义．
2．二倍角公式
S2α
sin 2α＝2sin_αcos_α；
变形：1＋sin 2α＝(sin α＋cos α)2，
1－sin 2α＝(sin α－cos α)2
C2α
cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α；
变形：cos2α＝，sin2α＝
T2α
tan 2α＝

3．辅助角公式
一般地，函数f(α)＝asin α＋bcos α(a，b为常数)可以化为f(α)＝sin(α＋φ)或f(α)＝cos(α－φ) .

[澄清盲点误点]
一、关键点练明
1．(正用二倍角公式)若sin α＝，则cos 2α＝(　　)
A.　　　　　　　　 B．
C．－ D．－
答案：B
2．(正用两角差的正切公式)已知tan α＝2，则tan＝________.
答案：
3．(逆用两角差的正弦公式)化简cos 18°cos 42°－cos 72°sin 42°的值为________．
答案：
4．(辅助角公式)cos 15°－4sin215°cos 15°＝________.
解析：cos 15°－4sin215°cos 15°＝cos 15°－2sin 15°·2sin 15°cos 15°＝cos 15°－2sin 15°·sin 30°＝cos 15°－sin 15°＝2cos(15°＋30°)＝2cos 45°＝.
答案：
二、易错点练清
1．(忽视角的范围)已知锐角α，β满足sin α＝，cos β＝，则α＋β＝(　　)
A.　　　　　　　　　 B．
C. D．或
解析：选B　因为α，β为锐角，且sin α＝<，cos β＝>，则cos α＝，且α∈，sin β＝且β∈，
所以sin(α＋β)＝sin α·cos β＋cos α·sin β＝×＋×＝.
又α＋β∈，所以α＋β＝.
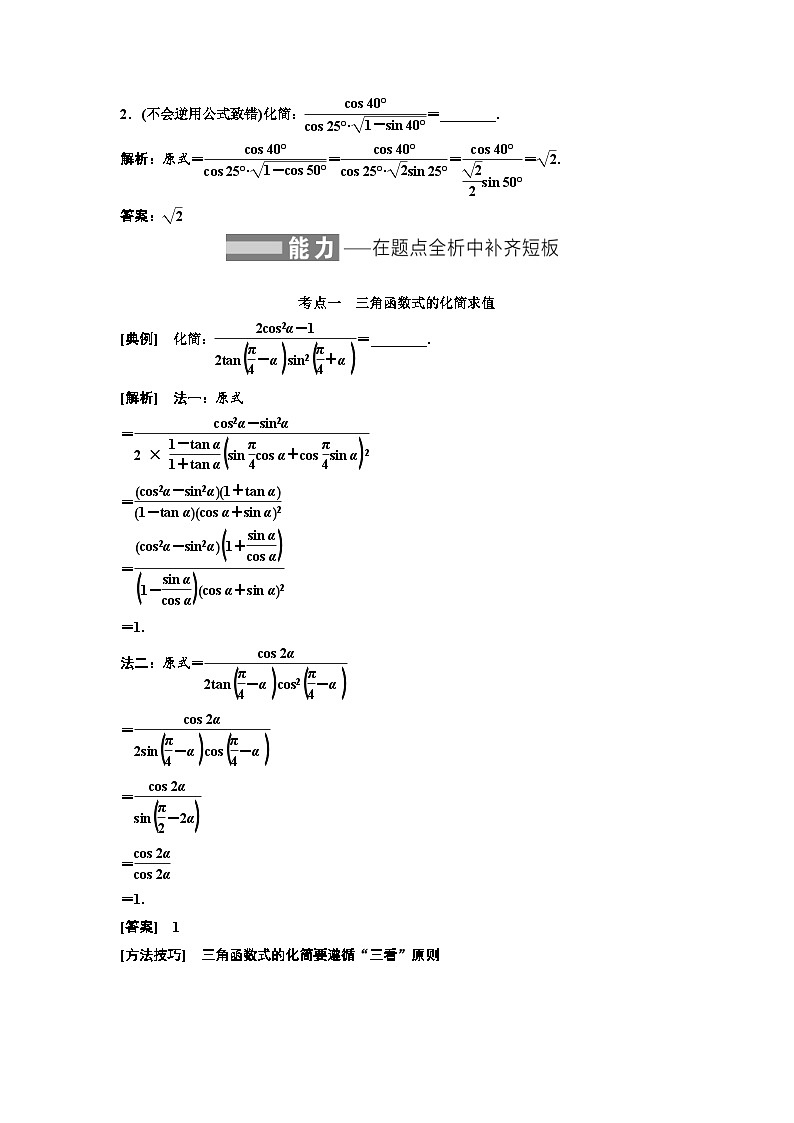
2．(不会逆用公式致错)化简：＝________.
解析：原式＝＝＝＝.
答案：


考点一　三角函数式的化简求值
[典例]　化简：＝________.
[解析]　法一：原式
＝
＝
＝
＝1.
法二：原式＝
＝
＝
＝
＝1.
[答案]　1
[方法技巧]　三角函数式的化简要遵循“三看”原则

　[提醒]　化简三角函数式的常见方法有弦切互化，异名化同名，异角化同角，降幂与升幂等．
[针对训练]
已知α∈(0，π)，化简：
.
解：原式＝.
因为α∈(0，π)，所以cos >0，
所以原式＝＝·＝cos2－sin2
＝cos α.
考点二　三角函数的求值
考法(一)　给值(角)求值
[例1]　(1)＝(　　)
A．－　　　　　　　　　 B．－
C. D．
(2)若α，β均为锐角且cos α＝，cos(α＋β)＝－，则sin＝(　　)
A．－ B．
C．－ D．
[解析]　(1)
＝
＝
＝sin 30°＝.
(2)∵α，β均为锐角，∴0<α＋β<π.
∵cos α＝，cos(α＋β)＝－，
∴sin α＝，sin(α＋β)＝.
∴cos β＝cos[(α＋β)－α]＝cos(α＋β)cos α＋sin(α＋β)sin α＝×＋×＝.
∴sin＝－cos 2β＝1－2cos2β＝.故选B.
[答案]　(1)C　(2)B
[方法技巧]
给值求值问题的求解思路
(1)化简所求式子．
(2)观察已知条件与所求式子之间的联系(从三角函数名及角入手)．
(3)将已知条件代入所求式子，化简求值．　　
考法(二)　给值求角
[例2]　已知A，B均为钝角，sin2＋cos＝，且sin B＝，则A＋B＝(　　)
A. B．
C. D．
[解析]　因为sin2＋cos＝，
所以＋cos A－sin A＝，
即－sin A＝，解得sin A＝.
因为A为钝角，
所以cos A＝－＝－ ＝－.
由sin B＝，且B为钝角，
可得cos B＝－＝－ ＝－.
所以cos(A＋B)＝cos Acos B－sin Asin B
＝×－×＝.
又A，B都为钝角，即A，B∈，
所以A＋B∈(π，2π)，故A＋B＝.故选C.
[答案]　C
[方法技巧]
给值求角问题的解题策略
(1)讨论所求角的范围．
(2)根据已知条件，选取合适的三角函数求值．
①已知正切函数值，选正切函数；
②已知正、余弦函数值，选正弦或余弦函数．若角的范围是，选正、余弦函数皆可；若角的范围是(0，π)，选余弦函数较好；若角的范围为，选正弦函数较好．
(3)由角的范围，结合所求三角函数值写出要求的角．　　
[针对训练]
1．(2020·全国卷Ⅰ)已知α∈(0，π)，且3cos 2α－8cos α＝5，则sin α＝(　　)
A.　　　 B．　　　　
C.　　　　 D.
解析：选A　∵3cos 2α－8cos α＝5，
∴3(2cos2α－1)－8cos α＝5，
即3cos2α－4cos α－4＝0，解得cos α＝－或cos α＝2(舍去)．
∵α∈(0，π)，∴sin α＝＝.故选A.
2．(2020·全国卷Ⅲ)已知2tan θ－tan＝7，则tan θ＝(　　)
A．－2 B．－1
C．1 D．2
解析：选D　由已知得2tan θ－＝7，解得tan θ＝2.
3．已知锐角α，β满足sin α＝，cos β＝，则α＋β等于(　　)
A. B．或
C. D．2kπ＋(k∈Z)
解析：选C　由sin α＝，cos β＝，且α，β为锐角，可知cos α＝，sin β＝，故cos(α＋β)＝cos αcos β－sin αsin β＝×－×＝，又0<α＋β<π，故α＋β＝.
4.的值是________．
解析：原式＝＝＝＝2.
答案：2
考点三　三角恒等变换的综合问题
[典例]　(2021·郑州五校联考)已知函数f(x)＝2sincos＋sin 2x＋a的最大值为1.
(1)求实数a的值；
(2)若将f(x)的图象向左平移个单位，得到函数g(x)的图象，求函数g(x)在区间上的最大值和最小值．
[解]　(1)f(x)＝2sincos＋sin 2x＋a＝sin＋sin 2x＋a＝ cos 2x＋sin 2x＋a＝2sin＋a，
易知2＋a＝1，则a＝－1.
(2)∵将f(x)的图象向左平移个单位，得到函数g(x)的图象，
∴g(x)＝f＝2sin－1
＝2sin－1，
∵x∈，∴2x＋π∈.
∴当2x＋π＝π，即sin＝时，g(x)取最大值－1；
当2x＋π＝π，即sin＝－1时，g(x)取最小值－3.
[方法技巧]
求函数周期、最值、单调区间的方法步骤
(1)利用三角恒等变换及辅助角公式把三角函数关系式化成y＝Asin(ωx＋φ)＋t或y＝Acos(ωx＋φ)＋t的形式；
(2)利用公式T＝(ω>0)求周期；
(3)根据自变量的范围确定ωx＋φ的范围，根据相应的正弦曲线或余弦曲线求值域或最值，另外求最值时，根据所给关系式的特点，也可换元转化为求二次函数的最值；
(4)根据正、余弦函数的单调区间列不等式求函数y＝Asin(ωx＋φ)＋t或y＝Acos(ωx＋φ)＋t的单调区间．　　
[针对训练]
设函数f(x)＝coscos x－sin2(π－x)－.
(1)求函数f(x)的最小正周期和单调递增区间；
(2)若f(α)＝－1，且α∈，求f的值．
解：(1)∵f(x)＝sin xcos x－sin2x－＝(sin 2x＋cos 2x)－1＝sin－1，
∴f(x)的最小正周期T＝＝π.
由2kπ－≤2x＋≤2kπ＋(k∈Z)，
得kπ－≤x≤kπ＋(k∈Z)，
∴f(x)的单调递增区间为(k∈Z)．
(2)∵f(α)＝sin－1＝－1，
∴sin＝.
由α∈知2α＋∈，
∴cos＝－.
∴f＝sin－1
＝sin－1
＝－1
＝×－1＝－.


一、创新思维角度——融会贯通学妙法
三角中的“拆角”“配角”技巧
三角函数的计算是高考一个重要的考点，对于一些角的计算问题除了掌握两角和与差的三角函数公式及倍角公式之外，还要掌握一些必要的“拆角”“配角”的技巧，抓住题设与结论中角的差异，利用公式，变不同的角为同角，实现角的转换，这样可以简化运算．“拆角”“配角”是连接题设条件与待求结论的纽带，是三角函数求值的一种常用方法．下面就三角函数求值中的“拆角”“配角”技巧作一些总结．
技巧(一)　利用特殊角进行“拆角”
[例1]　化简求值：.
[解]　原式＝
＝
＝＝－.
[名师微点]
利用特殊角，达到角的转换，从而巧妙化简求值．将80°拆成60°＋20°，看起来好像将问题复杂化了，但由于60°是特殊角，事实上问题变得简单了．　　
技巧(二)　直接利用所求角与已知角的关系进行“拆角”“配角”
[例2]　已知α为锐角，且cos＝，求cos α的值．
[解]　∵0<α<，∴<α＋<，
∴sin＝，
∴cos α＝cos＝coscos＋sinsin＝.
[名师微点]
此类问题不宜对已知角的三角函数用和(差)角公式展开，一般是根据已知角和所求角的关系进行“拆角”，将所求角用已知角表示，灵活处理已知、未知的关系．同时要注意角的范围，适时地将角的范围尽可能地缩小．　　
技巧(三)　利用所求角与已知角的关系，借助于诱导公式变形“拆、配”
[例3]　已知cos＝，≤α<，求cos的值．
[解]　∵≤α<，∴≤α＋<，
∵cos＝>0，∴α＋是第四象限角，
∴sin＝－，
∴sin α＝sin＝sincos－cossin＝＝－.
同理，cos α＝－，
∴cos＝cos＝coscos α－sinsin α＝×－×＝－.
[名师微点]
对于这类问题，主要是寻找已知和未知间的联系，这个联系就是解题的着手点，审题时要仔细分析条件与结论的关系，善于运用整体思想解题．本题将α＋看成一个整体，则2α＋可转化为＋α.那么，只需由条件求sin，sin α及cos α的值即可．而求 sin α时，再将α转化为－即可．　　
总之，在利用两角和(差)的余弦、正弦和正切公式时，不能机械地从表面上去套公式，而要变通地从本质上使用公式，分析已知条件和结论中角之间的相互关系，把所求的角拆分、配成某两个角(已知的两个角或者可以从已知的角简单变形就能得到的两个角)的和或差，并且这两个角的正、余弦函数值和正切函数值是已知的或可求的．
二、创新考查方式——领悟高考新动向
1．定义：＝ad－bc，如＝1×4－2×3＝－2，则＝(　　)
A．0　　　　　　　　　　 B．
C．－ D．1
解析：选C　由题意得＝cos 45°cos 105°－sin 75°sin 135°＝ －cos 45°cos 75°－sin 75°sin 45°＝－cos(75°－45°)＝－cos 30°＝－.

2．(多选)(2021·湘中名校联考)《九章算术》是我国古代内容极为丰富的数学名著，书中有一个“引葭赴岸”问题：“今有池方一丈，葭生其中央．出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何？”其意思为今有水池1丈见方(即CD＝10尺)，芦苇生长在水的中央，长出水面的部分为1尺．将芦苇向池岸牵引，恰巧与水岸齐接(如图所示)．试问水深、芦苇的长度各是多少？假设θ＝∠BAC，则下列四个结论中正确的是(　　)
A．水深为12尺 B．芦苇长为15尺
C．tan＝ D．tan＝－
解析：选ACD　设BC＝x，则AC＝x＋1，∵AB＝5，∴52＋x2＝(x＋1)2，∴x＝12，即水深为12尺，故芦苇长为13尺．
∴tan θ＝.由tan θ＝，
解得tan＝(负值已舍去)．
∵tan θ＝，∴tan＝＝－.
故正确的结论为A、C、D.
3.“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图)，若大、小正方形的面积分别为25和1，直角三角形中较大的锐角为θ，则cos 2θ等于(　　)
A. B．－
C. D．－
解析：选B　因为大正方形的面积为25，小正方形的面积为1，所以大正方形的边长为5，小正方形的边长为1，所以5sin θ－5cos θ＝1，即sin θ－cos θ＝，两边平方得1－ sin 2θ＝，即sin 2θ＝.因为θ是直角三角形中较大的锐角，所以<θ<，所以<2θ<π，所以cos 2θ＝－＝－.故选B.
4.如图，图中实线是由三段圆弧连接而成的一条封闭曲线C，各段弧所在的圆经过同一点P(点P不在C上)且三个圆半径相等，设第i段弧所对的圆心角为αi(i＝1,2,3)，则coscos－sinsin＝________.
解析：设三段圆弧交于A，B，D三点，连接PA，PB，PD，
则∠APB＋∠APD＋∠BPD＝2π，从而α1＋α2＋α3＝4π，
所以coscos－sinsin＝cos＝cos＝－.
答案：－

一、基础练——练手感熟练度
1．sin 45°cos 15°＋cos 225°sin 165°＝(　　)
A．1　　　　　　　　　　 B．
C. D．－
解析：选B　sin 45°cos 15°＋cos 225°sin 165°＝sin 45°·cos 15°＋(－cos 45°)sin 15°＝sin(45°－15°)＝sin 30°＝.
2．已知α∈，2sin 2α＝cos 2α＋1，则sin α＝(　　)
A. B．
C. D．
解析：选B　由二倍角公式可知4sin αcos α＝2cos2α.
∵α∈，∴cos α≠0，sin α>0，
∴2sin α＝cos α，又sin2α＋cos2α＝1，
∴sin α＝.故选B.
3．(2021·苏州模拟)若cos＝－，则cos＋cos α＝(　　)
A．－ B．±
C．－1 D．±1
解析：选C　cos＋cos α＝cos α＋sin α＋cos α＝cos α＋sin α＝ cos＝－1.
4．tan 18°＋tan 12°＋tan 18°tan 12°＝(　　)
A. B．
C. D．
解析：选D　∵tan 30°＝tan(18°＋12°)＝＝，∴tan 18°＋tan 12°＝(1－tan 18°tan 12°)，∴原式＝.
5．若α∈，且3cos 2α＝sin，则sin 2α的值为(　　)
A．－ B．
C．－ D．
解析：选C　由3cos 2α＝sin，可得3(cos2α－sin2α)＝(cos α－sin α)，又由α∈，可知cos α－sin α≠0，于是3(cos α＋sin α)＝，所以1＋2sin αcos α＝，故sin 2α＝－.
6．已知sin＝，α∈，则cos的值为________．
解析：由已知得cos α＝，sin α＝－，
所以cos＝cos α＋sin α＝－.
答案：－
二、综合练——练思维敏锐度
1．已知sin＝cos，则tan α＝(　　)
A．1 B．－1
C. D．0
解析：选B　∵sin＝cos，
∴cos α－sin α＝cos α－sin α，
即sin α＝cos α，
∴tan α＝＝－1.
2．(多选)下列各式中，值为的是(　　)
A. B．tan 15°cos215°
C.cos2－sin2 D．
解析：选ACD　∵＝tan 45°＝，
tan 15°·cos215°＝sin 15°cos 15°＝sin 30°＝，
cos2－sin2＝cos ＝，
＝sin 30°＝，∴选A、C、D.　
3．若sin(α＋β)＝，sin(α－β)＝，则的值为(　　)
A．5 B．－1
C．6 D．
解析：选A　由题意知sin αcos β＋cos αsin β＝，sin αcos β－cos αsin β＝，
所以sin αcos β＝，cos αsin β＝，所以＝5，即＝5.故选A.
4．(2020·全国卷Ⅲ)已知sin θ＋sin＝1，则sin＝(　　)
A. B．
C. D．
解析：选B　∵sin θ＋sin＝sin θ＋cos θ＝sin＝1，∴sin＝.故选B.
5．(2021·辽宁八校联考)已知cos＝3sin，则tan＝(　　)
A．4－2 B．2－4
C．4－4 D．4－4
解析：选B　由题意可得－sin α＝－3sin，即sin＝3sin，sinα＋·cos －cossin ＝3sincos ＋ 3cossin ，整理可得tan＝－2tan ＝－2tan＝ －2×＝2－4.故选B.
6.17世纪德国著名的天文学家开普勒曾经这样说过：“几何学里有两件宝，一个是勾股定理，另一个是黄金分割．如果把勾股定理比作黄金矿的话，那么可以把黄金分割比作钻石矿．”黄金三角形有两种，其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形，它是一个顶角为36°的等腰三角形(另一种是顶角为108°的等腰三角形)．例如，五角星由五个黄金三角形与一个正五边形组成，如图所示，在其中一个黄金△ABC中，＝.根据这些信息，可得sin 234°＝(　　)
A. B．－
C．－ D．－
解析：选C　由图可知，∠ACB＝72°，
且cos 72°＝＝，
∴cos 144°＝2cos272°－1＝－.
则sin 234°＝sin(144°＋90°)＝cos 144°＝－.
7．设当x＝θ时，函数f(x)＝sin x－2cos x取得最大值，则cos θ＝(　　)
A. B．
C．－ D．－
解析：选C　利用辅助角公式可得f(x)＝sin x－2cos x＝sin(x－φ)，其中cos φ＝，sin φ＝.当函数f(x)＝sin x－2cos x取得最大值时，θ－φ＝2kπ＋(k∈Z)，∴θ＝2kπ＋＋φ(k∈Z)，则cos θ＝cos＝－sin φ＝－(k∈Z)．故选C.
8．设0°<α<90°，若sin(75°＋2α)＝－，则sin(15°＋α)·sin(75°－α)＝(　　)
A. B．
C．－ D．－
解析：选B　因为0°<α<90°，所以75°<75°＋2α<255°.又因为sin(75°＋2α)＝－<0，所以180°<75°＋2α<255°，角75°＋2α为第三象限角，所以cos(75°＋2α)＝－.所以sin(15°＋α)sin(75°－α)＝sin(15°＋α)cos(15°＋α)＝sin(30°＋2α)＝sin[(75°＋2α)－45°]＝[sin(75°＋2α)·cos 45°－cos(75°＋2α)sin 45°]＝×－×＋×＝.故选B.
9．若sin 2α＝，sin(β－α)＝，且α∈，β∈，则α＋β的值是(　　)
A. B．
C.或 D．或
解析：选A　∵α∈，∴2α∈，
∵sin 2α＝>0，∴2α∈，
∴α∈且cos 2α＝－.
又∵sin(β－α)＝，β∈，
∴β－α∈，cos(β－α)＝－，
∴cos(α＋β)＝cos[(β－α)＋2α]
＝cos(β－α)cos 2α－sin(β－α)sin 2α
＝×－×＝，
又∵α＋β∈，∴α＋β＝.
10．化简：－＝________.
解析：－＝
＝＝＝4.
答案：4
11．已知α∈，β∈，且cos＝，sin＝－，则cos(α＋β)＝________.
解析：∵α∈，∴－α∈，
又cos＝，∴sin＝－.
∵sin＝－，∴sin＝.
又∵β∈，∴＋β∈，
∴cos＝，
∴cos(α＋β)＝cos
＝coscos＋sinsin
＝×－×＝－.
答案：－
12．已知方程x2＋3ax＋3a＋1＝0(a>1)的两根分别为tan α，tan β，且α，β∈，则α＋β＝________.
解析：依题意有
∴tan(α＋β)＝＝＝1.
又
∴tan α<0且tan β<0，
∴－<α<0且－<β<0，
即－π<α＋β<0，结合tan(α＋β)＝1，
得α＋β＝－.
答案：－
13．已知A，B均为锐角，cos(A＋B)＝－，cos＝－，则cos＝________.
解析：因为A，B均为锐角，cos(A＋B)＝－，cos＝－，所以 sin＝ ＝.
所以cos＝cos＝－×＋×＝.
答案：
14．已知函数f(x)＝2sin xcos x－2cos2x＋1(x∈R)．
(1)求函数f(x)的最小正周期及在区间上的最大值和最小值；
(2)若f(x0)＝，x0∈，求cos 2x0的值．
解：(1)由f(x)＝2sin xcos x－2cos2x＋1，
得f(x)＝(2sin xcos x)－(2cos2x－1)
＝sin 2x－cos 2x＝2sin，
∴函数f(x)的最小正周期为π.
易知f(x)＝2sin在区间上为增函数，
在区间上为减函数，
又f(0)＝－1，f＝2，f＝－1，
∴函数f(x)在上的最大值为2，最小值为－1.
(2)∵2sin＝，∴sin＝.
又x0∈，∴2x0－∈，
∴cos＝.
∴cos 2x0＝cos
＝coscos－sinsin
＝×－×＝.

15．持续高温使某市多地出现干旱，城市用水紧张，为了宣传节约用水，某人准备在一片扇形区域(如图1)上按照图2的方式放置一块矩形ABCD区域宣传节约用水，其中顶点B，C在半径ON上，顶点A在半径OM上，顶点D在上，∠MON＝，ON＝OM＝10 m，设∠DON＝θ，矩形ABCD的面积为S.

(1)用含θ的式子表示DC，OB的长；
(2)若此人布置1 m2的宣传区域需要花费40元，试将S表示为θ的函数，并求布置此矩形宣传栏最多要花费多少元钱？
解：(1)在△ODC中，DC＝10sin θ，
在△OAB中，OB＝＝10sin θ.
(2)在△ODC中OC＝10cos θ，
从而S＝BC×CD＝100(cos θsin θ－sin2θ)
＝100
＝100
＝100sin－50，0<θ<，
当2θ＋＝，即θ＝时，S取得最大值100－50≈13.4，
所以布置此矩形宣传栏最多要花费13.4×40＝536元．