

山东省淄博市2023年各地区中考考数学模拟(二模)试题按题型难易度分层分类汇编-03解答题(基础题)
展开山东省淄博市2023年各地区中考考数学模拟(二模)试题按题型难易度分层分类汇编-03解答题(基础题)
一.整式的混合运算(共1小题)
1.(2023•沂源县二模)(1)计算:;
(2)化简:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b).
二.分式的混合运算(共1小题)
2.(2023•周村区二模)已知 T=(a+)÷.
(1)化简T;
(2)若a、b为方程x2﹣x﹣6=0的两个根,求T的值.
三.分式的化简求值(共1小题)
3.(2023•博山区二模)先化简,再求值:,其中.
四.解一元一次不等式(共1小题)
4.(2023•周村区二模)解不等式:,并把它的解集在数轴上表示出来.
五.一元一次不等式组的整数解(共1小题)
5.(2023•高青县二模)解不等式组,并求它的整数解.
六.反比例函数与一次函数的交点问题(共1小题)
6.(2023•淄川区二模)如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象相交于A(1,3),B(3,n)两点,与两坐标轴分别相交于点P,Q,过点B作BC⊥OP于点C,连接OA.
(1)求一次函数和反比例函数的解析式;
(2)求四边形ABCO的面积.
七.平移的性质(共1小题)
7.(2023•博山区二模)如图,在△ABC中,BC=3,将△ABC平移4个单位长度得到△A1B1C1,点P,Q分别是AB,A1C1的中点,求PQ的最大值和最小值.
八.解直角三角形的应用(共1小题)
8.(2023•淄川区二模)如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知MO=4m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米,才能发现C处的儿童(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.)
九.解直角三角形的应用-方向角问题(共1小题)
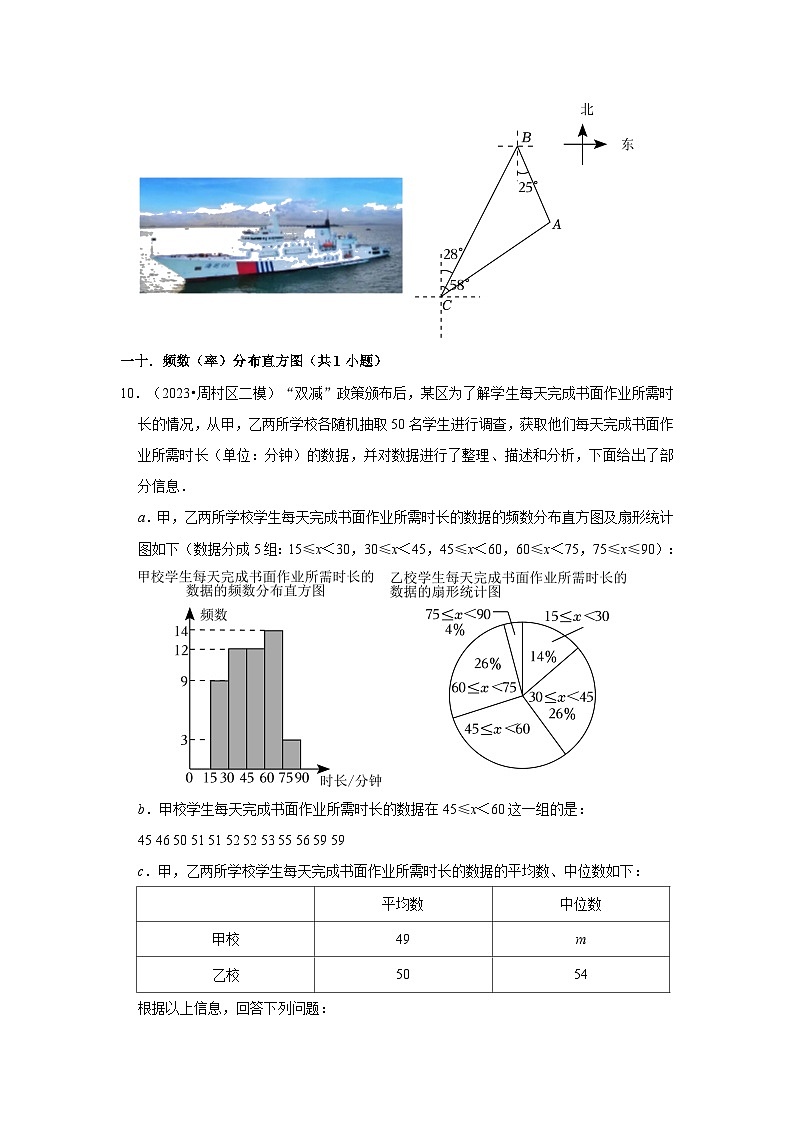
9.(2023•临淄区二模)在某海域开展的“海上联合”反潜演习中,我方军舰要到达C岛完成任务.已知军舰位于B市的南偏东25°方向上的A处,且在C岛的北偏东58°方向上,B市在C岛的北偏东28°方向上,且距离C岛372 km,此时,我方军舰沿着AC方向以30 km/h的速度航行,问:我方军舰大约需要多长时间到达C岛?(参考数据:,,,)
一十.频数(率)分布直方图(共1小题)
10.(2023•周村区二模)“双减”政策颁布后,某区为了解学生每天完成书面作业所需时长的情况,从甲,乙两所学校各随机抽取50名学生进行调查,获取他们每天完成书面作业所需时长(单位:分钟)的数据,并对数据进行了整理、描述和分析,下面给出了部分信息.
a.甲,乙两所学校学生每天完成书面作业所需时长的数据的频数分布直方图及扇形统计图如下(数据分成5组:15≤x<30,30≤x<45,45≤x<60,60≤x<75,75≤x≤90):
b.甲校学生每天完成书面作业所需时长的数据在45≤x<60这一组的是:
45 46 50 51 51 52 52 53 55 56 59 59
c.甲,乙两所学校学生每天完成书面作业所需时长的数据的平均数、中位数如下:
平均数
中位数
甲校
49
m
乙校
50
54
根据以上信息,回答下列问题:
(1)m= ;
(2)乙校学生每天完成书面作业所需时长的数据的扇形统计图中表示45≤x<60这组数据的扇形圆心角的度数是 °;
(3)小明每天完成书面作业所需时长为53分钟,在与他同校被调查的学生中,有一半以上的学生每天完成书面作业所需时长都超过了小明,那么小明是 校学生(填“甲”或“乙”),理由是 ;
(4)如果甲,乙两所学校各有1000人,估计这两所学校每天完成书面作业所需时长低于60分钟的学生共有 人.
一十一.条形统计图(共1小题)
11.(2023•淄川区二模)为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)该校抽查九年级学生的人数为 ,图①中的m值为 ;
(Ⅱ)求统计的这组数据的众数、中位数和平均数.
(Ⅲ)根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于2h的学生人数.
一十二.列表法与树状图法(共2小题)
12.(2023•临淄区二模)区内某学校为了开展好课后延时服务,举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五个兴趣小组(每人限报一项),将参加各兴趣小组的人数绘制成如图两幅不完整的统计图.
根据统计图中的信息解答下列问题:
(1)本次参加课后延时服务的学生人数是 名;
(2)把条形统计图补充完整;扇形统计图中的∠α的度数是 度;
(3)在C组最优秀的2名同学(1名男生1名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加全区的课后延时服务成果展示比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
13.(2023•高青县二模)春季开学后,某校为了让学生有效应用压岁钱,开展有意义的“尊老、敬老”慈善捐款活动,将捐款捐赠给本市敬老院.学生会为了了解学生捐款的情况,随机调查了该校部分学生,根据调查结果,绘制了两幅不完整的统计图.请根据相关信息,解答下列问题:
(1)本次调查的学生人数为 人,在扇形统计图中,捐款金额为100元所在扇形的圆心角的度数是 度,在调查的这组学生中,捐款金额的中位数是 元;
(2)补全条形统计图;
(3)学生会为了更好地引导学生合理支配压岁钱,选出甲,乙,丙和丁四人从不同的方面在全校进行讲解,但由于时间的限定,临时调整只能两人讲解.因此,学生会采用随机抽签的方式从甲,乙,丙和丁四人中确定两名讲解人选.请用列表或画树状图的方式说明抽中甲和乙的概率是多少?
山东省淄博市2023年各地区中考考数学模拟(二模)试题按题型难易度分层分类汇编-03解答题(基础题)
参考答案与试题解析
一.整式的混合运算(共1小题)
1.(2023•沂源县二模)(1)计算:;
(2)化简:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b).
【答案】(1)﹣1;(2)4﹣5ab﹣3a3b2.
【解答】解:(1)原式=
=3﹣3﹣1
=﹣1;
(2)原式=4﹣a2+a2﹣5ab﹣3a3b2
=4﹣5ab﹣3a3b2.
二.分式的混合运算(共1小题)
2.(2023•周村区二模)已知 T=(a+)÷.
(1)化简T;
(2)若a、b为方程x2﹣x﹣6=0的两个根,求T的值.
【答案】(1)a+b;
(2)1.
【解答】解:(1)T=•
=a+b;
(2)∵a、b为方程x2﹣x﹣6=0的两个根,
∴a+b=1,
∴T=1.
三.分式的化简求值(共1小题)
3.(2023•博山区二模)先化简,再求值:,其中.
【答案】,.
【解答】解:
=•
=
=
=,
当时,原式==.
四.解一元一次不等式(共1小题)
4.(2023•周村区二模)解不等式:,并把它的解集在数轴上表示出来.
【答案】x<3,数轴见解析.
【解答】解:x﹣,
去分母得:4x﹣2(x+1)<4﹣(x﹣3),
去括号得:4x﹣2x﹣2<4﹣x+3,
移项合并得:3x<9,
系数化为1得:x<3.
在数轴上表示为:
五.一元一次不等式组的整数解(共1小题)
5.(2023•高青县二模)解不等式组,并求它的整数解.
【答案】﹣1<x≤4,原不等式组的整数解是0,1,2,3,4.
【解答】解:
解不等式①,得:x≤4,
解不等式②,得:x>﹣1,
∴不等式组的解集是﹣1<x≤4.
∴原不等式组的整数解是0,1,2,3,4.
六.反比例函数与一次函数的交点问题(共1小题)
6.(2023•淄川区二模)如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象相交于A(1,3),B(3,n)两点,与两坐标轴分别相交于点P,Q,过点B作BC⊥OP于点C,连接OA.
(1)求一次函数和反比例函数的解析式;
(2)求四边形ABCO的面积.
【答案】(1)反比例函数的解析式为y=,一次函数的解析式为y=﹣x+4;
(2).
【解答】解:(1)∵反比例函数y=(x>0)的图象过A(1,3),
∴m=1×3=3,
∴反比例函数的解析式为y=,
把B(3,n)点代入得,n==1,
∴B(3,1),
把A(1,3),B(3,1)代入y=kx+b得,解得,
∴一次函数的解析式为y=﹣x+4;
(2)作AM⊥x轴于M,则S△AOM=×3=,
∵S四边形ABCO=S△AOM+S梯形AMCB,
∴S四边形ABCO=+×(3+1)(3﹣1)=.
七.平移的性质(共1小题)
7.(2023•博山区二模)如图,在△ABC中,BC=3,将△ABC平移4个单位长度得到△A1B1C1,点P,Q分别是AB,A1C1的中点,求PQ的最大值和最小值.
【答案】PQ的最大值为5.5,最小值为2.5.
【解答】解:取A1B1的中点P′,连接QP′、PP′,如图,
∵△ABC平移4个单位长度得到△A1B1C1,
∴PP′=4,B1C1=BC=3,
∵Q是A1C1的中点,P′为A1B1的中点,
∴P′Q为△A1B1C1的中位线,
∴P′Q=1.5,
∴PP′﹣P′Q≤PQ≤PP′+P′Q(当且仅当P、P′、Q三点共线时取等号),
即4﹣1.5≤PQ≤4+1.5,
∴PQ的最小值为2.5,
∴PQ的最大值为5.5,最小值为2.5.
八.解直角三角形的应用(共1小题)
8.(2023•淄川区二模)如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知MO=4m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米,才能发现C处的儿童(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.)
【答案】汽车从A处前行约6米,才能发现C处的儿童.
【解答】解:在Rt△CMO中,MO=4 m,CO=5 m,
∴CM===3(m),
∵∠BOD=∠MOC,∠BDO=∠CMO=90°,
∴△BDO∽△CMO,
∴,
∴,
∴BD=2.25m,
在Rt△AOD中,∠AOD=70°,
∴AD=OD•tan70°≈3×2.75=8.25(m),
∴AB=AD﹣BD=8.25﹣2.25=6(m),
∴汽车从A处前行约6米,才能发现C处的儿童.
九.解直角三角形的应用-方向角问题(共1小题)
9.(2023•临淄区二模)在某海域开展的“海上联合”反潜演习中,我方军舰要到达C岛完成任务.已知军舰位于B市的南偏东25°方向上的A处,且在C岛的北偏东58°方向上,B市在C岛的北偏东28°方向上,且距离C岛372 km,此时,我方军舰沿着AC方向以30 km/h的速度航行,问:我方军舰大约需要多长时间到达C岛?(参考数据:,,,)
【答案】10h.
【解答】解:过点A作AD⊥BC于D,
由题意得,∠ACB=58°﹣28°=30°,∠ABC=28°+25°=53°,BC=372km,
设AD=xkm,
在Rt△ABD中,
∵∠ABD=53°,
∴BD=≈=,
在Rt△ACD中,
∵∠ACD=30°,
∴CD===,
∵BC=BD+CD,
∴,
解得x≈150,
即AD=150km,
∴AC=2AD=300km,
∵300÷30=10(h),
∴我方军舰大约需要10h到达C岛.
一十.频数(率)分布直方图(共1小题)
10.(2023•周村区二模)“双减”政策颁布后,某区为了解学生每天完成书面作业所需时长的情况,从甲,乙两所学校各随机抽取50名学生进行调查,获取他们每天完成书面作业所需时长(单位:分钟)的数据,并对数据进行了整理、描述和分析,下面给出了部分信息.
a.甲,乙两所学校学生每天完成书面作业所需时长的数据的频数分布直方图及扇形统计图如下(数据分成5组:15≤x<30,30≤x<45,45≤x<60,60≤x<75,75≤x≤90):
b.甲校学生每天完成书面作业所需时长的数据在45≤x<60这一组的是:
45 46 50 51 51 52 52 53 55 56 59 59
c.甲,乙两所学校学生每天完成书面作业所需时长的数据的平均数、中位数如下:
平均数
中位数
甲校
49
m
乙校
50
54
根据以上信息,回答下列问题:
(1)m= 51 ;
(2)乙校学生每天完成书面作业所需时长的数据的扇形统计图中表示45≤x<60这组数据的扇形圆心角的度数是 108 °;
(3)小明每天完成书面作业所需时长为53分钟,在与他同校被调查的学生中,有一半以上的学生每天完成书面作业所需时长都超过了小明,那么小明是 乙 校学生(填“甲”或“乙”),理由是 53分钟低于乙校学生每天完成书面作业所需时长中位数54分钟 ;
(4)如果甲,乙两所学校各有1000人,估计这两所学校每天完成书面作业所需时长低于60分钟的学生共有 1360 人.
【答案】(1)51;
(2)108;
(3)乙,53分钟低于乙校学生每天完成书面作业所需时长中位数54分钟;
(4)1360.
【解答】(1)解:甲校50名学生每天完成书面作业的中位数是第25、26个数,都是51,
∴,
故答案为:51;
(2)解:乙校学生每天完成书面作业所需时长的数据的扇形统计图中表示45≤x<60这组数据的扇形圆心角的度数是360°×(1﹣14%﹣26%﹣26%﹣4%)=108°,
故答案为:108;
(3)解:甲校中位数是51,乙校中位数是54,
而小明每天完成书面作业所需时长为53分钟,在与他同校被调查的学生中,有一半以上的学生每天完成书面作业所需时长都超过了小明,
∴小明是乙校学生,因为53分钟低于乙校学生每天完成书面作业所需时长中位数54分钟;
故答案为:乙,53分钟低于乙校学生每天完成书面作业所需时长中位数54分钟;
(4)解:样本中,甲校每天完成书面作业所需时长低于60分钟的学生有9+12+12=33人,
乙校每天完成书面作业所需时长低于60分钟的学生有50×(1﹣26%﹣4%)=35人,
∴甲校1000名学生每天完成书面作业所需时长低于60分钟的学生有人,
乙校1000名学生每天完成书面作业所需时长低于60分钟的学生有人,
∴估计这两所学校每天完成书面作业所需时长低于60分钟的学生共有660+700=1360人.
故答案为:1360.
一十一.条形统计图(共1小题)
11.(2023•淄川区二模)为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)该校抽查九年级学生的人数为 40 ,图①中的m值为 25 ;
(Ⅱ)求统计的这组数据的众数、中位数和平均数.
(Ⅲ)根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于2h的学生人数.
【答案】见试题解答内容
【解答】解:(Ⅰ)该校抽查九年级学生的人数为:4÷10%=40(人),
∵m%=×100%=25%,
∴m=25,
故答案为:40,25;
(Ⅱ)∵在这组数据中3小时出现次数最多,有15次,
∴众数为3小时;
在这50个数据中,中位数为第25、26个数据的平均数,即中位数为=3小时;
平均数是:(1×4+2×8+3×15+4×10+5×3)=3(小时);
( III)根据题意得:
400×=280(人),
答:根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于2h的约有280人.
一十二.列表法与树状图法(共2小题)
12.(2023•临淄区二模)区内某学校为了开展好课后延时服务,举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五个兴趣小组(每人限报一项),将参加各兴趣小组的人数绘制成如图两幅不完整的统计图.
根据统计图中的信息解答下列问题:
(1)本次参加课后延时服务的学生人数是 80 名;
(2)把条形统计图补充完整;扇形统计图中的∠α的度数是 72 度;
(3)在C组最优秀的2名同学(1名男生1名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加全区的课后延时服务成果展示比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
【答案】(1)80.
(2)补全条形统计图见解答;72.
(3).
【解答】解:(1)本次参加课后延时服务的学生人数是18÷22.5%=80(名).
故答案为:80.
(2)参加D组的人数为80﹣16﹣18﹣20﹣8=18(名).
补全条形统计图如图所示.
扇形统计图中的∠α的度数是360°×=72°.
故答案为:72.
(3)设C组的1名男生和1名女生分别记为a,b,E组的2名男生和1名女生分别记为c,d,e,
画树状图如下:
共有6种等可能的结果,其中所选两名同学中恰好是1名男生1名女生的结果有:ae,bc,bd,共3种,
∴所选两名同学中恰好是1名男生1名女生的概率为=.
13.(2023•高青县二模)春季开学后,某校为了让学生有效应用压岁钱,开展有意义的“尊老、敬老”慈善捐款活动,将捐款捐赠给本市敬老院.学生会为了了解学生捐款的情况,随机调查了该校部分学生,根据调查结果,绘制了两幅不完整的统计图.请根据相关信息,解答下列问题:
(1)本次调查的学生人数为 60 人,在扇形统计图中,捐款金额为100元所在扇形的圆心角的度数是 108 度,在调查的这组学生中,捐款金额的中位数是 50 元;
(2)补全条形统计图;
(3)学生会为了更好地引导学生合理支配压岁钱,选出甲,乙,丙和丁四人从不同的方面在全校进行讲解,但由于时间的限定,临时调整只能两人讲解.因此,学生会采用随机抽签的方式从甲,乙,丙和丁四人中确定两名讲解人选.请用列表或画树状图的方式说明抽中甲和乙的概率是多少?
【答案】(1)60,108,50;
(2)见解析;
(3).
【解答】解:(1)∵捐款金额为50元的有21人,所占的百分比为35%,
∴这次被调查的学生共有:21÷35%=60(人);
捐款金额为100元所在扇形的圆心角的度数是:;
捐款金额的中位数是第30、31两个数,即50元;
故答案为:60,108,50;
(2)捐款金额为20元对应人数为:60×20%=12(人)
捐款金额为200元对应人数为:60﹣3﹣12﹣21﹣18=6(人);
补全条形统计图如图.
(3)解:画树状图得:
∵共有12种等可能的情况,恰好选中甲、乙两位同学的有2种,
∴P(选中甲、乙)=.
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题),共26页。试卷主要包含了÷÷,其中x为不等式组的整数解,,如图所示,两点,且对称轴为直线x=4等内容,欢迎下载使用。
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题),共26页。试卷主要包含了÷÷,其中x为不等式组的整数解,,如图所示,两点,且对称轴为直线x=4等内容,欢迎下载使用。
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(基础题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(基础题),共24页。试卷主要包含了﹣1;,小明解方程﹣=1的过程如下,计算,解不等式组等内容,欢迎下载使用。












