专题19 二次函数与特殊角问题专项练习

这是一份专题19 二次函数与特殊角问题专项练习，文件包含专题19二次函数与特殊角问题原卷版docx、专题19二次函数与特殊角问题解析版docx等2份试卷配套教学资源，其中试卷共98页， 欢迎下载使用。
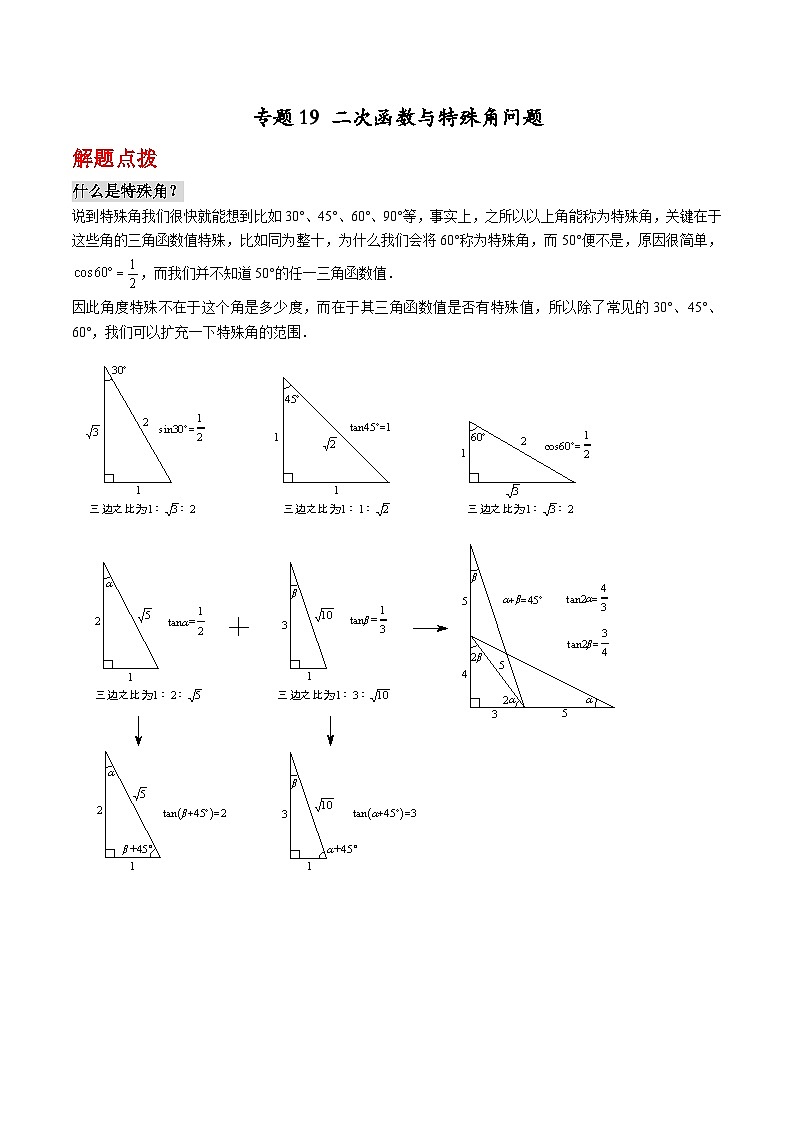
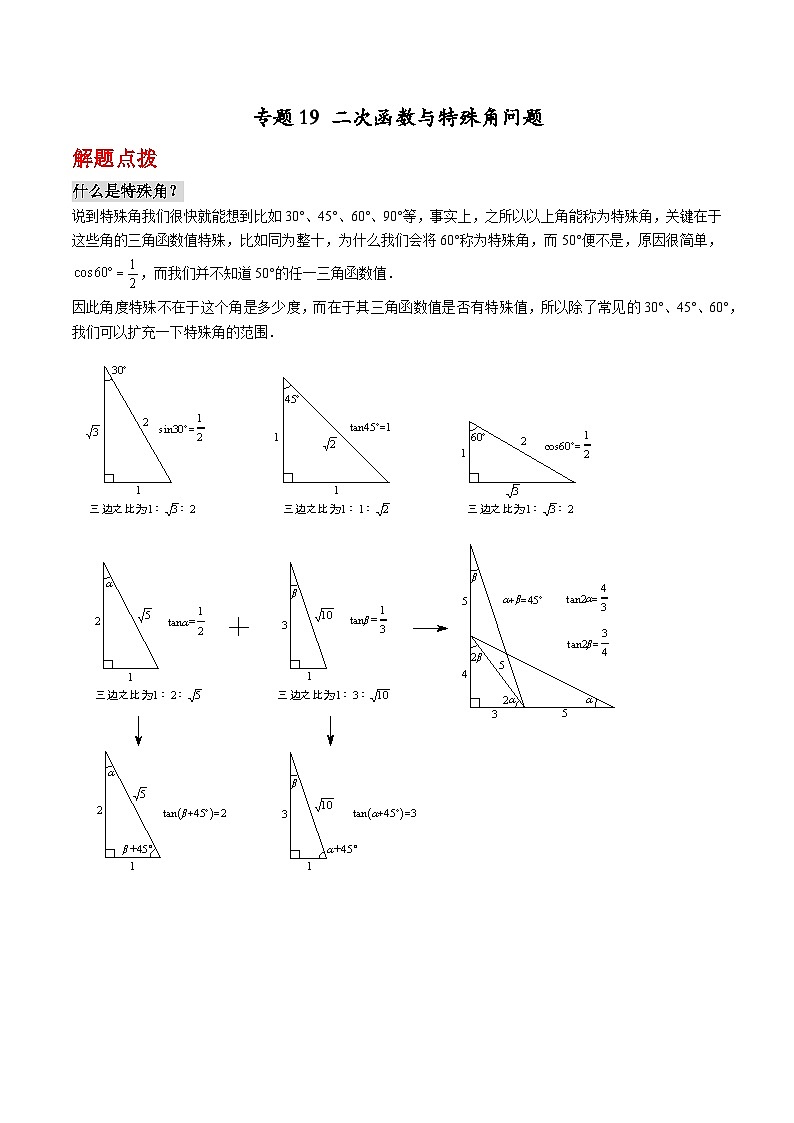
专题19 二次函数与特殊角问题解题点拨什么是特殊角？说到特殊角我们很快就能想到比如30°、45°、60°、90°等，事实上，之所以以上角能称为特殊角，关键在于这些角的三角函数值特殊，比如同为整十，为什么我们会将60°称为特殊角，而50°便不是，原因很简单，，而我们并不知道50°的任一三角函数值．因此角度特殊不在于这个角是多少度，而在于其三角函数值是否有特殊值，所以除了常见的30°、45°、60°，我们可以扩充一下特殊角的范围．
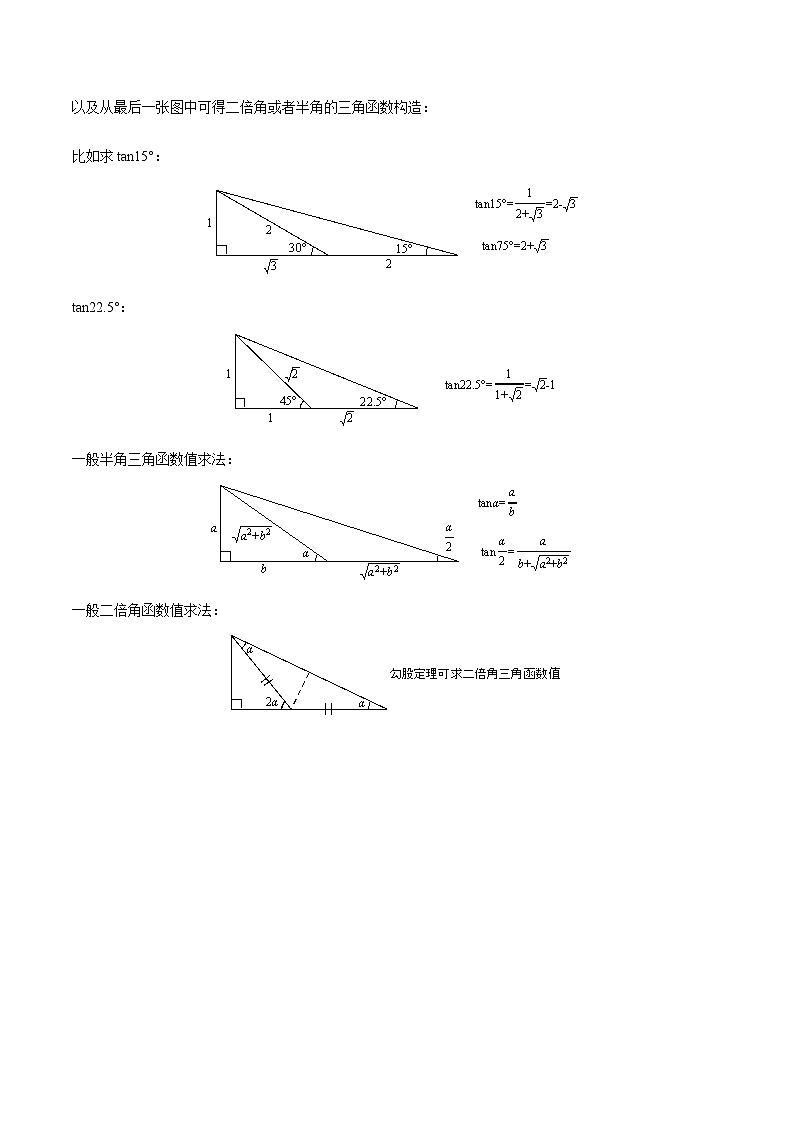
以及从最后一张图中可得二倍角或者半角的三角函数构造： 比如求tan15°：tan22.5°：一般半角三角函数值求法：一般二倍角函数值求法：
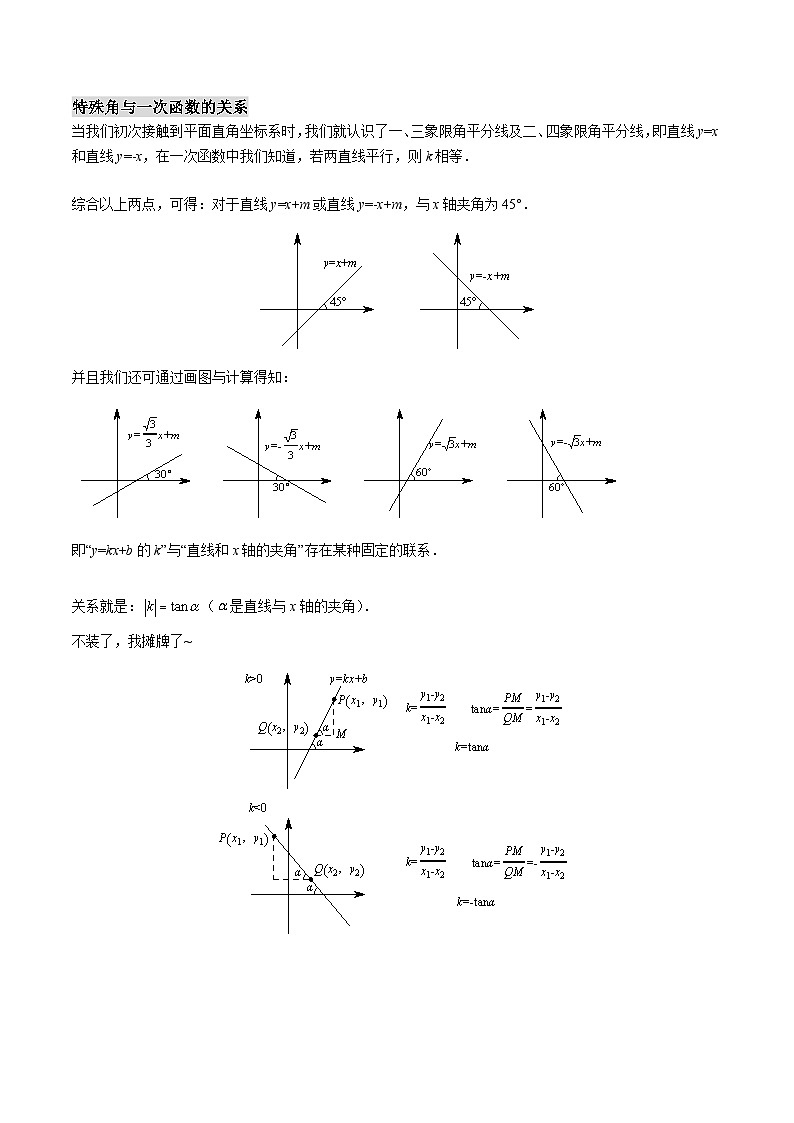
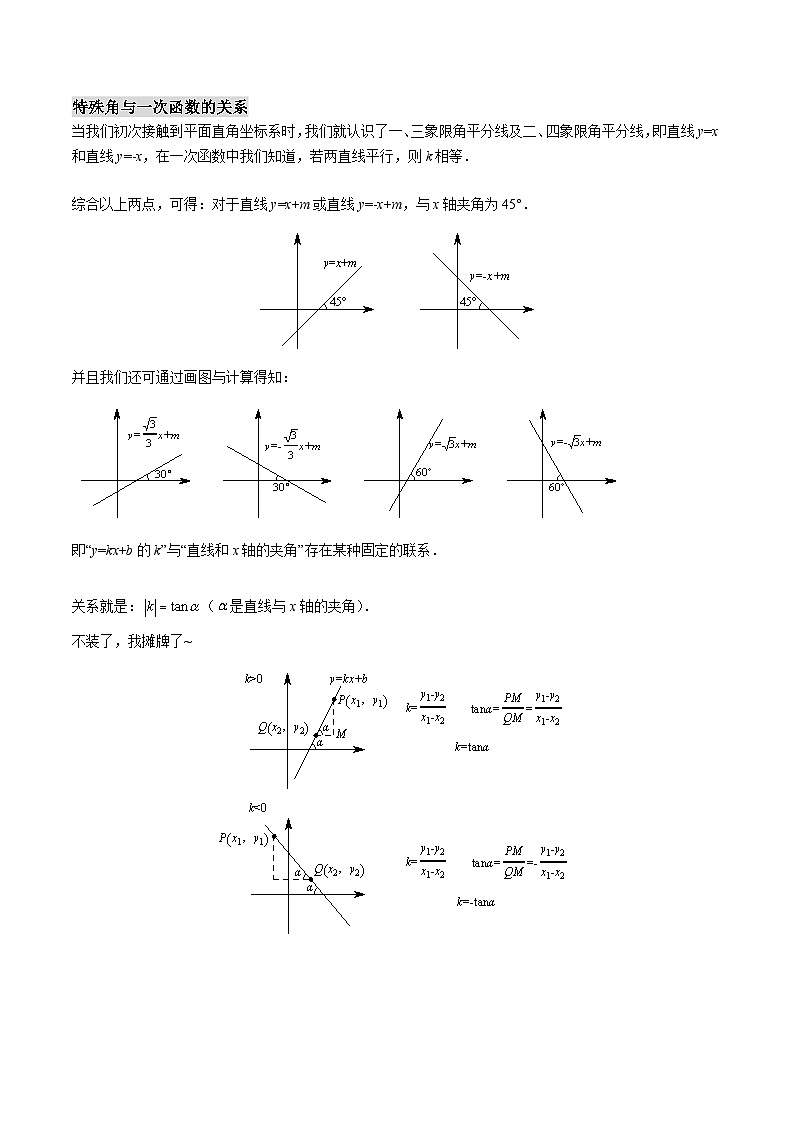
特殊角与一次函数的关系当我们初次接触到平面直角坐标系时，我们就认识了一、三象限角平分线及二、四象限角平分线，即直线y=x和直线y=-x，在一次函数中我们知道，若两直线平行，则k相等． 综合以上两点，可得：对于直线y=x+m或直线y=-x+m，与x轴夹角为45°．并且我们还可通过画图与计算得知：即“y=kx+b的k”与“直线和x轴的夹角”存在某种固定的联系． 关系就是：（是直线与x轴的夹角）．不装了，我摊牌了~  
坐标系中特殊角的处理方法在坐标系中构造定角，从其三角函数值着手：思路1：构造三垂直相似（或全等）；思路2：通过三角函数值化“角度条件”为“直线k”．引例1：如图，在平面直线坐标系中，直线AB解析式为，点M（2，1）是直线AB上一点，将直线AB绕点M顺时针旋转45°得到直线CD，求CD解析式．【分析】思路1：构造三垂直相似（全等）在坐标系中存在45°角，可作垂直即可得到等腰直角三角形，构造三垂直全等确定图形．在直线AB上取一点O，过点O作OP⊥AB交CD于P点，分别过M、P向x轴作垂线，垂足为E、F点．易证△OEM≌△PFO，故PF=OE=2，OF=ME=1，故P点坐标为（-1，2），结合P、M坐标可解直线CD解析式：．构造等腰直角的方式也不止这一种，也可过点O作CD的垂线，但直角顶点未知的情况计算略难于直角顶点已知的情况，故虽可以做但并不推荐．思路2：利用特殊角的三角函数值．过M点作MN∥x轴，则，，考虑到直线CD的增减性为y随着x的增大而减小，故，所以直线CD：，化简得：． 引例2：如图，在平面直线坐标系中，直线AB解析式为，点M（2，1）是直线AB上一点，将直线AB绕点M顺时针旋转得到直线CD，且，求直线CD解析式．【分析】在直线AB上再选取点O构造三垂直相似，如下图所示， 易证△PFO∽△OEM，且相似比，即，，故P点坐标为，结合P、M点坐标可解直线CD解析式：． 本题并不容易从三角函数值本身下手，原因在于角度并不属于我们所讨论的特殊角范围之内，简便的做法只存在于特殊的角中． 认识特殊角，了解特殊角，运用特殊角，就能在复杂问题中找到简便的求法．直击中考1．如图，已知顶点为的抛物线与轴交于，两点，直线过顶点和点．（1）求的值；（2）求函数的解析式；（3）抛物线上是否存在点，使得？若存在，求出点的坐标；若不存在，请说明理由．
2．已知抛物线经过点和点，与y轴交于点C，点P为第二象限内抛物线上的动点．(1)抛物线的解析式为___________，抛物线的顶点坐标为___________．(2)如图1，是否存在点P，使四边形的面积为9？若存在，请求出点Р的坐标；若不存在，请说明理由．(3)如图2，连接交于点，当时，请直接写出点D的坐标；(4)如图3，点E的坐标为，点C为x轴负半轴上的一点，，连接PE，若，请求出点Р的坐标．
3．（2022·全国·九年级专题练习）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+6（a≠0）交x轴于A、B两点，交y轴于点C，且OA＝OC＝3OB，连接AC．(1)求抛物线的表达式；(2)点P从点C以每秒2个单位长度的速度沿CA运动到点A，点Q从点O以每秒1个单位长度的速度沿OC运动到点C，点P和点Q同时出发，连接PQ，当点P到达点A时，点Q停止运动，求S△CPQ的最大值及此时点P的坐标；(3)抛物线上是否存在点M，使得∠ACM＝15°？若存在，求出点M的坐标；若不存在，请说明理由．
4．（2022·广东·模拟预测）如图，点B，C分别在x轴和y轴的正半轴上，OB，OC的长分别为x2-8x+12=0的两个根（OC＞OB），点A在x轴的负半轴上，且OA=OC=3OB，连接AC．(1)求过A，B，C三点的抛物线的函数解析式；(2)点P从点C出发，以每秒2个单位长度的速度沿CA运动到点A，点Q从点O出发，以每秒1个单位长度的速度沿OC运动到点C，连接PQ，当点P到达点A时，点Q停止运动，求S△CPQ的最大值；(3)M是抛物线上一点，是否存在点M，使得∠ACM=15°？若存在，请求出点M的坐标；若不存在，请说明理由．
5．如图1，二次函数的图像与x轴交于点A(﹣2，0)，B(4，0)，抛物线的顶点为C，作射线AC，BC．动点P从点A出发，以每秒1个单位长度的速度沿射线AC做匀速运动，动点Q从B出发，以每秒2个单位长度的速度沿射线BC运动．(1)填空：b＝_____，c＝_____，C的坐标为_____．(2)点P，Q运动过程中，△CPQ可能为等腰三角形吗？说明理由．(3)如图2，连接PO，QO，当∠POQ＝30°时，直接写出t的值．
6．（2021秋·浙江湖州·九年级统考期末）已知地物线与轴交于点，点在该抛物线上（1）若抛物线的对称轴是直线，请用含的式子表示；（2）如图1，过点作轴的垂线段，垂足为点．连结和，当为等边三角形时，求抛物线解析式；（3）如图2，在（2）条件下，已知为轴上的一动点，连结和，当时，求满足条件的点的坐标．
7．如图所示，在平面直角坐标系中，抛物线的顶点坐标为，并与y轴交于点，点A是对称轴与x轴的交点．(1)求抛物线的解析式；(2)如图①所示，P是抛物线上的一个动点，且位于第一象限，连接，求的面积的最大值；(3)如图②所示，在对称轴的右侧作交抛物线于点D，求出D点的坐标；并探究：在y轴上是否存在点Q，使？若存在，求点Q的坐标；若不存在，请说明理由．
8．如图，已知抛物线的顶点M（0，4），与x轴交于A（－2，0）、B两点，(1)求抛物线的解析式；(2)如图1，点C（0，2），P为抛物线上一点，过点P作PQy轴交直线BC于Q（P在Q上方），再过点P作PRx轴交直线BC于点R，若△PQR的面积为2，求P点坐标；(3)如图2，在抛物线上是否存在一点D，使∠MAD＝45°，若存在，求出D点坐标，若不存在，请说明理由．
9．如图，在平面直角坐标系中，已知抛物线与x轴交于、两点，与y轴交于点C，连接AC，(1)求抛物线的解析式；(2)在对称轴上是否存在一点M，使，若存在，请求出点M的坐标；若不存在，请说明理由；(3)①若点P是直线AC下方的抛物线上的一个动点，作PD⊥AC于点D，当PD的值最大时，求此时点P的坐标及PD的最大值；②若点P是抛物线上的一个动点，且∠APB＝45°，请直接写出点P的横坐标．
10．（2023·山东济南·九年级期末）如图1，线的图象经过点，交轴于点、（A点在点左侧），顶点为．(1)求抛物线的解析式；(2)如图2，在直线上方的抛物线上，过点作轴的平行线交于点，过点作轴的平行线交轴于点，过点作轴的平行线交轴于点，求矩形的周长最大值；(3)抛物线的对称轴上是否存在点，使？若存在，请直接写出点的纵坐标；若不存在，请说明理由．
11．（2021·新疆乌鲁木齐·二模）如图，抛物线过点，且与直线交于B、C两点，点B的坐标为．（1）求抛物线的解析式；（2）点D为抛物线上位于直线上方的一点，过点D作轴交直线于点E，点P为对称轴上一动点，当线段的长度最大时，求的最小值；（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使？若存在，求点Q的坐标；若不存在，请说明理由．
12．如图，在直角坐标系中，四边形OABC是平行四边形，经过A（﹣2，0），B，C三点的抛物线y＝ax2+bx+（a＜0）与x轴的另一个交点为D，其顶点为M，对称轴与x轴交于点E．（1）求这条抛物线对应的函数表达式；（2）已知R是抛物线上的点，使得△ADR的面积是平行四边形OABC的面积的，求点R的坐标；（3）已知P是抛物线对称轴上的点，满足在直线MD上存在唯一的点Q，使得∠PQE＝45°，求点P的坐标．
13．（2022·辽宁葫芦岛·二模）如图，在平面直角坐标系中，二次函数的图象与坐标轴交于A，B，C三点，其中点A的坐标为（-3，0），点B的坐标为（0，-4），连接AB，BC． 动点P从点A出发，在线段AB上以每秒1个单位长度的速度向点B作匀速运动；同时，动点Q从点A出发，在线段AC上以每秒个单位长度的速度向点C作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒． 连接PQ，PC． (1)求抛物线的表达式；(2)在点P，Q运动过程中，当的面积为时，求点Q坐标；(3)在（2）条件下，时，在直线PQ上是否存在点M，使？若存在，请直接求出点M的坐标；若不存在，请说明理由．
14．如图1，在平面直角坐标系中，一次函数的图像经过点A(，m)，与y轴交于点B，与x轴交于点C．抛物线经过点A交y轴于点D(0，6)．(1)求m的值及抛物线的表达式；(2)如图2，点E为抛物线上一点且在直线AC上方，若EAC的面积为，求出点E的坐标；(3)坐标轴上有一动点F，连接AF，当∠BAF=60°时，直接写出点F的坐标．
15．（2023·全国·九年级专题练习）如图，在二次函数（m是常数，且）的图像与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．其对称轴与线段BC交于点E，与x轴交于点F．连接AC，BD．(1)求A，B，C三点的坐标（用数字或含m的式子表示），并求的度数；(2)若，求m的值；(3)若在第四象限内二次函数（m是常数，且）的图像上，始终存在一点P，使得，请结合函数的图像，直接写出m的取值范围．
16．（2022秋·云南曲靖·九年级校联考期中）如图，已知抛物线交x轴于，两点，交y轴于点C，点P是抛物线上一点，连接AC、BC．(1)求抛物线的表达式；(2)连接OP，BP，若，求点P的坐标；(3)在抛物线的对称轴上是否存在点Q，使得∠QBA＝75°？若存在，直接写出点Q的坐标；若不存在，请说明理由．
17．（2021·贵州六盘水·统考二模）如图，二次函数y＝﹣x2+bx+c的图象与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C．(1)求二次函数的表达式；(2)将直线BC向上平移h（h＞0）个单位长度，当直线BC与二次函数y＝﹣x2+bx+c的图象只有1个交点时，求h的值；(3)在二次函数图象的对称轴上，是否存在点P，使得∠PBA＝75°？若存在，直接写出点P的坐标；若不存在，请说明理由．
18．（2022·黑龙江齐齐哈尔·三模）如图，二次函数的图象交x轴于点A、点B，其中点B的坐标为，点C的坐标为，过点A、C的直线交二次函数的图象于点D．(1)求二次函数和直线的函数表达式；(2)连接，则的面积为________；(3)在y轴上确定点Q，使得，点Q的坐标为________；(4)点M是抛物线上一点，点N为平面上一点，是否存在这样的点N，使得以点A、点D、点M、点N为顶点的四边形是以为边的矩形？若存在，请你直接写出点N的坐标；若不存在，请说明理由．
19．（2022·辽宁大连·九年级期末）函数y＝，其中a是常数且a≠0，该函数的图象记为G．(1)图象G经过3个定点，分别为 　   　，　   　，　   　；(2)图象G与直线y＝a有2个交点时，结合函数图象，求a的值；(3)图象G与直线x＝2和直线x＝﹣2分别相交于点P，Q，当∠POQ＝135°时，直接写出a的值．
20．（2022·陕西西安·高新一中校考模拟预测）如图，已知抛物线，与轴交于点，点与轴交于点，抛物线的顶点为，其对称轴与轴交于点．(1)抛物线解析式为______，顶点的坐标为______；(2)判断的形状，并说明理曲；(3)如图，点是线段上的一个动点（点与点、点不重合），连结、，过点作，射线交射线于点，交抛物线于点；过点作，垂足为点，交射线于点．①当≌时，请求出此时点的坐标；②当时，请你直接写出的值．