

新高考数学二轮复习培优讲义03 不等式(含解析)
展开解密03讲 :不等式
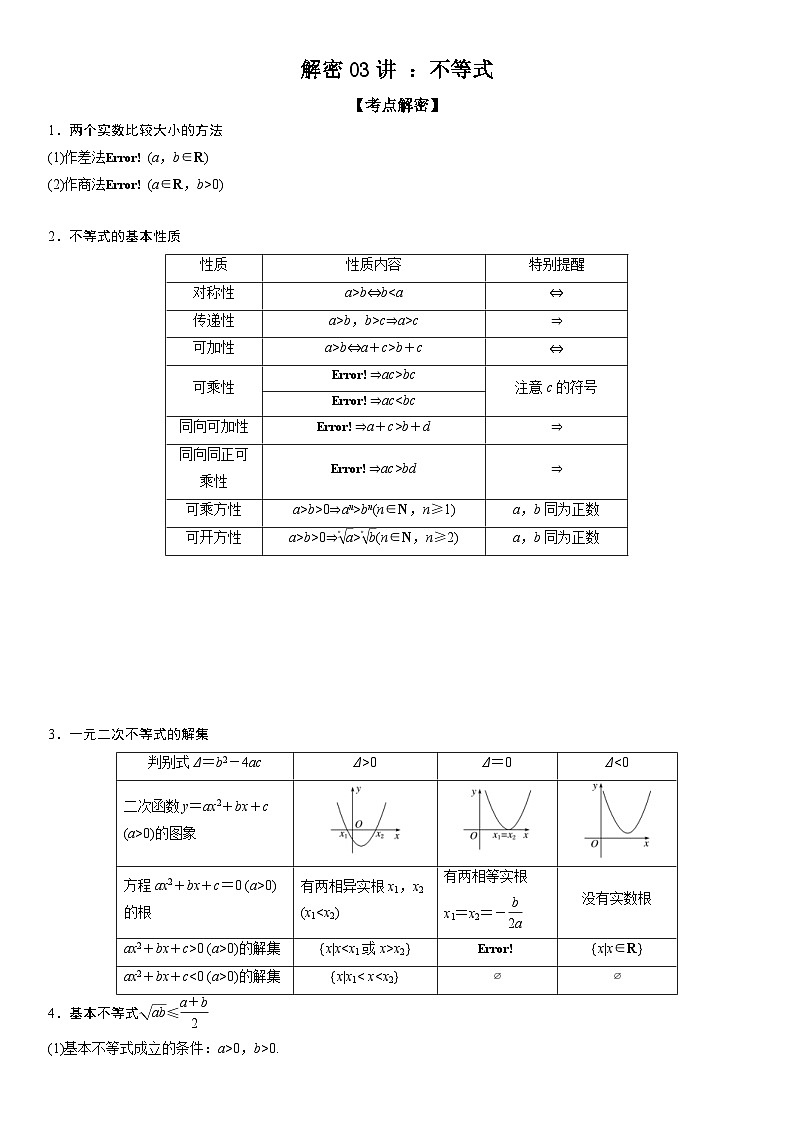
【考点解密】
1.两个实数比较大小的方法
(1)作差法 (a,b∈R)
(2)作商法 (a∈R,b>0)
2.不等式的基本性质
性质
性质内容
特别提醒
对称性
a>b⇔b
传递性
a>b,b>c⇒a>c
⇒
可加性
a>b⇔a+c>b+c
⇔
可乘性
⇒ac>bc
注意c的符号
⇒ac
⇒a+c>b+d
⇒
同向同正可乘性
⇒ac>bd
⇒
可乘方性
a>b>0⇒an>bn(n∈N,n≥1)
a,b同为正数
可开方性
a>b>0⇒>(n∈N,n≥2)
a,b同为正数
3.一元二次不等式的解集
判别式Δ=b2-4ac
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c (a>0)的图象
方程ax2+bx+c=0 (a>0)的根
有两相异实根x1,x2
(x1
x1=x2=-
没有实数根
ax2+bx+c>0 (a>0)的解集
{x|x
{x|x∈R}
ax2+bx+c<0 (a>0)的解集
{x|x1< x
∅
4.基本不等式≤
(1)基本不等式成立的条件:a>0,b>0.
(2)等号成立的条件:当且仅当a=b时取等号.
(3)其中叫做正数a,b的算术平均数,叫做正数a,b的几何平均数.
5.几个重要的不等式
(1)a2+b2≥2ab(a,b∈R).
(2)+≥2(a,b同号).
(3)ab≤2(a,b∈R).
(4)≥2(a,b∈R).
以上不等式等号成立的条件均为a=b.
6.用基本不等式求最值
用基本不等式≤求最值应注意:一正二定三相等.
(1)a,b是正数;
(2)①如果ab等于定值P,那么当a=b时,和a+b有最小值2;
②如果a+b等于定值S,那么当a=b时,积ab有最大值S2.
(3)讨论等号成立的条件是否满足.
【方法技巧】
一、比较大小的常用方法
(1)作差法:①作差;②变形;③定号;④得出结论.
(2)作商法:①作商;②变形;③判断商与1的大小关系;④得出结论.
(3)构造函数,利用函数的单调性比较大小.
二、判断不等式的常用方法
(1)直接利用不等式的性质逐个验证,利用不等式的性质判断不等式是否成立时要特别注意前提条件.
(2)利用特殊值法排除错误答案.
(3)利用函数的单调性,当直接利用不等式的性质不能比较大小时,可以利用指数函数、对数函数、幂函数等函数的单调性来比较.
三、利用基本不等式求最值
(1)前提:“一正”“二定”“三相等”.
(2)要根据式子的特征灵活变形,配凑出积、和为常数的形式,然后再利用基本不等式.
(3)条件最值的求解通常有三种方法:一是配凑法;二是将条件灵活变形,利用常数“1”代换的方法;三是消元法.
【核心题型】
题型一:比较两个数(式)的大小
1.已知,,,则,,的大小关系为( )
A. B. C. D.
【答案】B
【分析】通过作差法,,确定符号,排除D选项;
通过作差法,,确定符号,排除C选项;
通过作差法,,确定符号,排除A选项;
【详解】由,且,故;
由且,故;
且,故.
所以,
故选:B.
2.已知:,则3,,的大小关系是( )
A. B.
C. D.
【答案】D
【分析】先将指数式化为对数式,再根据对数函数单调性以及运算法则比较大小,确定选项.
【详解】,,
∴;
又 ,∴.故选D.
【点睛】本题考查指数式化与对数式关系以及对数函数单调性,考查基本分析求解能力,属基础题.
3.设,,则与的大小关系是( )
A. B. C. D.无法确定
【答案】A
【分析】利用作差法解出的结果,然后与0进行比较,即可得到答案
【详解】解:因为,,
所以,
∴,
故选:A
题型二:不等式的基本性质
4.对于实数a,b,c,下列命题中正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
【答案】D
【分析】由不等式性质判断各选项正误即可.
【详解】对于选项A,注意到若,当时,.故A错误.
对于选项B,设,
得,解得.又,,
得.故B错误.
对于C选项,因,则,故C错误.
对于D选项,,因,则,故D正确.
故选:D
5.已知a,b,c,d均为实数,则下列命题正确的是( )
A.若a>b,c>d,则a-d>b-c B.若a>b,c>d则ac>bd
C.若ab>0,bc-ad>0,则 D.若a>b,c>d>0,则
【答案】AC
【分析】根据不等式的性质和特殊值法逐项分析可求得答案.
【详解】解:由不等式性质逐项分析:
A选项:由,故,根据不等式同向相加的原则,故A正确
B选项:若,则,故B错误;
C选项:,,则,化简得,故C正确;
D选项:,,,则,故D错误.
故选:AC
6.已知,则 ( )
A. B.
C. D.
【答案】AC
【分析】对A,对两边同除ab化简即可判断;
对B,对不等式移项进行因式分解得,即可进一步判断的符号不确定,即可判断;
对C,对不等式移项进行因式分解得,由即可判断;
对D,对不等式移项进行根式运算得,即可进一步判断
【详解】对A,,A正确;
对B,,∵,∴,不等式不一定成立,B错误;
对C,,∵,∴,不等式成立,C正确;
对D,,所以,不等式不成立,D错误;
故选:AC.
题型三:不等式性质的综合应用
7.已知,,则的取值范围是( )
A. B. C. D.
【答案】D
【分析】利用待定系数法得出,并计算出的取值范围,利用不等式的性质可得出的取值范围.
【详解】设,,解得,
,
,,,
由不等式的性质可得,即,
因此,的取值范围是,故选D.
【点睛】本题考查求代数式的取值范围,解题的关键就是将所求代数式用已知的代数式加以表示,在求解可充分利用待定系数法,考查运算求解能力,属于中等题.
8.已知,,则的取值范围是( )
A. B. C. D.
【答案】C
【分析】利用待定系数法求得,由,,结合,从而可得结果.
【详解】令
则,
∴,
又,…∴①
,
∴…②
∴①②得.
则.
故选C.
【点睛】本题主要考查不等式的性质以及指数函数的性质,意在考查综合运用所学知识解答问题的能力,属于中档题.
9.已知,,则的取值范围为__________.
【答案】
【分析】由可以推出,由不等式的性质可以得到的取值范围.
【详解】,而,根据不等式的性质可得
,所以的取值范围为.
【点睛】本题考查了不等式的性质.不等式的性质中没有相除性,可以利用相乘性进行转化,但是应用不等式相乘性时,要注意不等式的正负性.
题型四:利用基本不等式求最值
命题点1 配凑法
10.设实数满足,函数的最小值为( )
A. B. C. D.6
【答案】A
【解析】将函数变形为,再根据基本不等式求解即可得答案.
【详解】解:由题意,所以,
所以
,
当且仅当,即时等号成立,
所以函数的最小值为.
故选:A.
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方
11.已知x>0,y>0,2x+3y=6,则xy的最大值为________.
【答案】
【详解】因为x>0,y>0,2x+3y=6,
所以xy=(2x·3y)≤·2=·2=.
当且仅当2x=3y,即x=,y=1时,xy取到最大值.
12.已知a>b>c,求(a-c)的最小值.
【详解】(a-c)
=(a-b+b-c)
=1+1++.
∵a>b>c,∴a-b>0,b-c>0,
∴2++≥2+2=4,
当且仅当a-b=b-c,即2b=a+c时取等号,
∴(a-c)的最小值为4.
命题点2常数代换法
13.已知,则的最小值是( )
A.7 B. C.4 D.
【答案】D
【分析】由“1”的妙用和基本不等式可求得结果.
【详解】因为,
所以,
当且仅当即时,等号成立.
结合可知,当时,有最小值.
故选:D.
14.已知,且,则的最小值为( )
A.9 B.10 C.11 D.
【答案】A
【分析】利用“乘1法”将问题转化为求的最小值,然后展开利用基本不等式求解.
【详解】,,又,且,
,
当且仅当,解得,时等号成立,
故的最小值为9.
故选:A.
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
15.若实数,则的最小值为( )
A. B.1 C. D.2
【答案】D
【分析】由条件变形,再结合基本不等式求最小值.
【详解】由条件可知,,
所以
,
当,即,结合条件 ,
可知时,等号成立,所以的最小值为.
故选:D
16.已知,且,则的最小值为_________.
【答案】4
【分析】根据已知条件,将所求的式子化为,利用基本不等式即可求解.
【详解】,,
,当且仅当=4时取等号,
结合,解得,或时,等号成立.
故答案为:
【点睛】本题考查应用基本不等式求最值,“1”的合理变换是解题的关键,属于基础题.
命题点3 消元法
17.负实数、满足,则的最小值为( )
A. B. C. D.
【答案】A
【分析】由已知可得,再利用基本不等式可求得的最小值.
【详解】因为负实数、满足,则,可得,
由基本不等式可得,
当且仅当时,即当时,等号成立.
故的最小值为.
故选:A.
18.若实数x,y满足xy+3x=3,则+的最小值为________.
【答案】8
【详解】∵实数x,y满足xy+3x=3,
∴x=,∴0<<,解得y>3.
则+=y+3+=y-3++6≥2+6=8,当且仅当y=4,x=时取等号.
19.已知,则的最小值是( )
A. B. C. D.2
【答案】B
【分析】依题意可得,又,即可得到,从而得到,利用基本不等式计算可得;
【详解】因为,所以,
因为,所以,
所以,
当且仅当,即,时取等号,
所以的最小值是;
故选:B
题型五:基本不等式的综合应用
20.已知正实数a、b满足,若的最小值为4,则实数m的取值范围是( )
A. B. C. D.
【答案】B
【分析】由题意可得=,当,即时等号成立,所以有,将化为,再利用基本不等式可求得的范围.
【详解】解:因为为正实数,
=,
当,即时等号成立,
此时有,
又因为,
所以,
由基本不等式可知(时等号成立),
所以.
故选:B.
21.在中,角所对的边分别为,且点满足,若,则的最大值为( )
A. B. C. D.
【答案】A
【分析】利用向量知识可得,两边平方可得,再利用不等式知识可求得结果.
【详解】因为,所以,所以,
所以,
所以,整理得,
所以,
因为,所以,
所以,解得.
所以的最大值为
故选:A
【点睛】关键点点睛:将向量条件化为,利用向量数量积的运算律运算得到是解题关键.
22.设等差数列{an}的公差为d,其前n项和是Sn,若a1=d=1,则的最小值是________.
【答案】
【详解】an=a1+(n-1)d=n,Sn=,
所以==≥=,
当且仅当n=,即n=4时取等号,
所以的最小值是.
【高考必刷】
一、单选题
1.(2021·山西太原·高一阶段练习)已知, ,则 和的大小关系为( )
A. B. C. D.
【答案】D
【分析】利用作差法,令,结果配方,判断符号后得出结论.
【详解】,
故有,
故选:D.
【点睛】本题考查用比较法证明不等式的方法,作差﹣﹣变形﹣﹣判断符号﹣﹣得出结论涉及完全平方公式的应用.属于基础题.
2.(2022·湖北·葛洲坝中学高一阶段练习)已知,则的大小关系是( )
A. B. C. D.不能确定
【答案】A
【分析】作差法比较大小,即得解
【详解】由题意,
因此
故选:A
【点睛】本题考查了作差法比较大小,考查了学生综合分析,数学运算能力,属于基础题
3.(2022·江苏宿迁·高一期中)若且,则下列不等式一定成立的是( )
A. B. C. D.
【答案】B
【分析】利用不等式的性质,通过举特例结合作差法比较大小即可判断各个选项正误.
【详解】对于A,当时,,,显然A错误;
对于B,∵且,∴,,
∴,
∴,即B正确;
对于C:当,时,,,显然C错误;
对于D:当时,,,显然D错误;
故选:B.
4.(2022·江西·贵溪市实验中学高三阶段练习(文))若,则的最大值为( )
A.1 B. C. D.
【答案】C
【解析】化简函数,利用基本不等式求出最值,并验证取等条件.
【详解】,
当且仅当,即时取等号
则的最大值为
故选:C
【点睛】本题考查基本不等式的应用,考查学生计算能力,属于中档题.
5.(2022·黑龙江·牡丹江市第三高级中学高三阶段练习)已知为正实数且,则的最小值为( )
A. B. C. D.3
【答案】D
【分析】由题知,再结合基本不等式求解即可.
【详解】解:因为为正实数且,
所以,
所以,
因为,当且仅当时等号成立;
所以,当且仅当时等号成立;
故选:D
6.(2022·全国·高三专题练习)已知两个正实数,满足,则的最小值是( )
A. B. C.8 D.3
【答案】A
【分析】根据题中条件,得到,展开后根据基本不等式,即可得出结果.
【详解】因为正实数满足,
则,
当且仅当,即时,等号成立.
故选:.
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
7.(2022·全国·高一单元测试)已知正数、满足,则的最小值为( )
A. B. C. D.
【答案】B
【分析】由得,再将代数式与相乘,利用基本不等式可求出
的最小值.
【详解】,所以,,
则,
所以,,
当且仅当,即当时,等号成立,
因此,的最小值为,
故选.
【点睛】本题考查利用基本不等式求最值,对代数式进行合理配凑,是解决本题的关键,属于中等题.
8.(2022·浙江·高一期中)已知实数,且,则的最小值是( )
A.6 B. C. D.
【答案】B
【分析】构造,利用均值不等式即得解
【详解】,
当且仅当,即,时等号成立
故选:B
【点睛】本题考查了均值不等式在最值问题中的应用 ,考查了学生综合分析,转化划归,数学运算能力,属于中档题
9.(2021·安徽合肥·高一期末)已知 ,且,则的最小值为( )
A. B. C. D.
【答案】C
【分析】运用乘1法,可得由x+y=(x+1)+y﹣1=[(x+1)+y]•()﹣1,化简整理再由基本不等式即可得到最小值.
【详解】由x+y=(x+1)+y﹣1
=[(x+1)+y]•1﹣1
=[(x+1)+y]•2()﹣1
=2(21
≥3+47.
当且仅当x,y=4取得最小值7.
故选C.
【点睛】本题考查基本不等式的运用:求最值,注意乘1法和满足的条件:一正二定三等,考查运算能力,属于中档题.
10.(2022·黑龙江·哈尔滨市第一中学校高一阶段练习)下列说法正确的是( )
A.若且,则至少有一个大于2
B.
C.若,则
D.若,则
【答案】A
【分析】结合反证法、全称量词命题、不等式、函数解析式的求法等知识求得正确答案.
【详解】A选项,依题意,且,若都不大于,即,
则,与已知矛盾,所以至少有一个大于,A选项正确.
B选项,当时,,所以B选项错误.
C选项,由于,所以,
所以,所以C选项错误.
D选项,依题意,①,
以替换得②,
由①②解得,所以D选项错误.
故选:A
11.(2022·甘肃省会宁县第一中学高一期中)若函数在处取最小值,则等于( )
A.3 B. C. D.4
【答案】A
【分析】将函数的解析式配凑为,再利用基本不等式求出该函数的最小值,利用等号成立得出相应的值,可得出的值.
【详解】当时,,则
,
当且仅当时,即当时,等号成立,因此,,故选A.
【点睛】本题考查基本不等式等号成立的条件,利用基本不等式要对代数式进行配凑,注意“一正、二定、三相等”这三个条件的应用,考查计算能力,属于中等题.
12.(2015·湖南·高考真题(文))若实数满足,则的最小值为( )
A. B.2 C. D.4
【答案】C
【详解】,(当且仅当时取等号),所以的最小值为,故选C.
考点:基本不等式
【名师点睛】基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,因此可以用在一些不等式的证明中,还可以用于求代数式的最值或取值范围.如果条件等式中,同时含有两个变量的和与积的形式,就可以直接利用基本不等式对两个正数的和与积进行转化,然后通过解不等式进行求解.
13.(2022·山东·青岛二中高一期中)十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用,后来英国资学家哈利奥特首次使用“>”和“<”符号,并逐步被数学界接受志不等号的引入对不等式的发展景响深远.已知a,b为非零实数,且;则下列结论正确的是( )
A. B. C. D.
【答案】D
【分析】根据各项不等式,利用作差法、特殊值,结合不等式性质判断正误即可.
【详解】A:,若有、,故,错误;
B:,若有、,故,错误;
C:若,则,错误;
D:,故,正确.
故选:D
14.(2022·福建·福州第十五中学高三阶段练习)已知且,则的取值范围是( )
A. B. C. D.
【答案】C
【分析】首先求得及的取值范围,再把转化为关于的代数式,利用函数的单调性去求的取值范围即可解决
【详解】由,可得,
则,则,令,则
,
又在单调递增,在单调递减
,,
则,即
故选:C
15.(2021·山西·太原市第五十六中学校高一阶段练习)若正数满足,当取得最小值时,的值为( )
A. B.2 C. D.5
【答案】B
【分析】将方程变形 代入可得3x+4y=(3x+4y)()=×3,然后利用基本不等式即可求解.
【详解】∵x+3y=5xy,x>0,y>0
∴
∴3x+4y=(3x+4y)()=×3
当且仅当即x=2y=1时取等号,的值为2.
故答案为B.
【点睛】本题考查了“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.解决二元的范围或者最值问题,常用的方法有:不等式的应用,二元化一元的应用,线性规划的应用,等.
16.(2022·全国·高三专题练习)当时,不等式恒成立,则的取值范围是( )
A. B. C. D.
【答案】A
【分析】由题可得,且,利用基本不等式解答即可.
【详解】解:∵,∴,
∴
当且仅当,即时取等号,
∵当时,不等式恒成立,
∴只需.
∴的取值范围为:.
故选A.
【点睛】本题主要考查基本不等式,解题的关键是得出,属于一般题.
17.(2022·天津·静海一中高一期中)已知正数、满足,若不等式恒成立,则实数的取值范围是( )
A. B. C. D.
【答案】C
【分析】由已知可得出,将与相乘,利用基本不等式可求得的最小值,即可得出实数的取值范围.
【详解】因为,,则,,
所以,,
所以,
当且仅当时,即,时等号成立.
又恒成立,所以.
故选:C.
18.(2022·福建·莆田一中高一阶段练习)已知,,若不等式恒成立,则实数的最大值为( )
A.10 B.9 C.8 D.7
【答案】C
【解析】由已知可得,即求的最小值,由基本不等式可得答案.
【详解】因为,,则,
所以,
当且仅当即等号成立,要使不等式恒成立,所以
所以实数的最大值为8.
故选:C.
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
二、多选题
19.(2022·全国·高一单元测试)下列命题为真命题的是( )
A.若,,则 B.若,,则
C.若,则 D.若,,则
【答案】AD
【分析】A.由不等式的性质判断;B.举例判断;C.由判断; D.作差判断.
【详解】A.由不等式的性质可知同向不等式相加,不等式方向不变,故正确;
B. 当时,,故错误;
C.当时,故错误;
D.,因为,,,所以,故正确;
故选:AD
20.(2022·河南省浚县第一中学高一阶段练习)若正实数a,b满足则下列说法正确的是( )
A.ab有最大值 B.有最大值
C.有最小值2 D.有最大值
【答案】AB
【解析】对A,根据基本不等式求的最大值;
对B,对平方再利用基本不等式求最大值;
对C,根据再展开求解最小值;
对D,对平方再根据基本不等式求最值.
【详解】对A,,当且仅当时取等号.故A正确.
对B, ,故,当且仅当时取等号.故B正确.
对C, .当且仅当时取等号.所以有最小值4.故C错误.
对D, ,即,故有最小值.故D错误.
故选:AB
【点睛】本题主要考查了基本不等式求解最值的问题,需要根据所给形式进行合适的变形,再利用基本不等式.属于中档题.
三、填空题
21.(2022·山东·乳山市银滩高级中学高一阶段练习)若实数满足,,则的取值范围为________.
【答案】
【分析】设,解得,,再由不等式的性质即可求解.
【详解】设,解得,
所以.
又,,,
所以.
故答案为:.
【点睛】关键点点睛:本题考查利用不等式的性质求取值范围,变形是解题的关键,考查学生的运算求解能力,属于基础题.
22.(2018·天津·高考真题(理))已知,且,则的最小值为_____________.
【答案】
【分析】由题意首先求得的值,然后结合均值不等式的结论整理计算即可求得最终结果,注意等号成立的条件.
【详解】由可知,
且:,因为对于任意,恒成立,
结合均值不等式的结论可得:.
当且仅当,即时等号成立.
综上可得的最小值为.
【点睛】在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.
23.(2023·广东·惠来县第一中学高一期中)已知,则的最大值为________.
【答案】1
【分析】直接利用基本不等式求最大值.
【详解】,则,
当且仅当即时取等号.
故答案为:
24.(2022·天津市第四中学高三期中)已知且,则的最小值为___________.
【答案】
【分析】令,,将已知条件简化为;将用表示,分离常数,再使用“乘1法”转化后利用基本不等式即可求得最小值.
【详解】解:令,,因为,所以,
则,,所以,
所以
,
当且仅当,即,,即时取“”,
所以的最小值为.
故答案为:.
25.(2019·天津·高考真题(文)) 设,,,则的最小值为__________.
【答案】.
【分析】把分子展开化为,再利用基本不等式求最值.
【详解】由,得,得
,
等号当且仅当,即时成立.
故所求的最小值为.
【点睛】使用基本不等式求最值时一定要验证等号是否能够成立.
26.(2017·天津·高考真题(文))若,,则的最小值为___________.
【答案】4
【详解】 ,(前一个等号成立条件是,后一个等号成立的条件是,两个等号可以同时取得,则当且仅当时取等号).
【考点】均值不等式
【名师点睛】利用均指不等式求最值要灵活运用两个公式,(1) ,当且仅当时取等号;(2) , ,当且仅当时取等号;首先要注意公式的使用范围,其次还要注意等号成立的条件;另外有时也考查利用“等转不等”“作乘法”“1的妙用”求最值.
27.(2017·江苏·高考真题)某公司一年购买某种货物吨,每次购买吨,运费为万元/次,一年的总存储费用为万元.要使一年的总运费与总存储费用之和最小,则的值是__________.
【答案】
【详解】总费用为,当且仅当,即时等号成立.故答案为30.
点睛:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.
28.(2022·全国·高考真题(理))已知中,点D在边BC上,.当取得最小值时,________.
【答案】
【分析】设,利用余弦定理表示出后,结合基本不等式即可得解.
【详解】[方法一]:余弦定理
设,
则在中,,
在中,,
所以
,
当且仅当即时,等号成立,
所以当取最小值时,.
故答案为:.
[方法二]:建系法
令 BD=t,以D为原点,OC为x轴,建立平面直角坐标系.
则C(2t,0),A(1,),B(-t,0)
[方法三]:余弦定理
设BD=x,CD=2x.由余弦定理得
,,
,,
令,则,
,
,
当且仅当,即时等号成立.
[方法四]:判别式法
设,则
在中,,
在中,,
所以,记,
则
由方程有解得:
即,解得:
所以,此时
所以当取最小值时,,即.
四、解答题
29.(2022·海南·儋州川绵中学高一期中)比较下列两组代数式的大小
(1)和
(2)与
【答案】(1);(2).
【分析】(1)利用作差比较法进行求解即可;
(2)利用作差比较法,结合配方法进行求解即可.
【详解】(1)
(2)
30.(2022·河北·衡水市冀州区滏运中学高一阶段练习)已知,,求,的取值范围.
【答案】的取值范围是,的取值范围是.
【分析】根据题意可得,进而得到的范围,再根据分数的性质可得的取值范围.
【详解】因为,所以.
又,
所以,
即.
因为,所以,
因为,所以,
所以,
即.
所以的取值范围是,的取值范围是.
31.(2022·江苏·北大附属宿迁实验学校高一阶段练习)已知,,分别求
(1)
(2)
(3)的取值范围.
【答案】(1);(2);(3).
【分析】利用不等式的性质进行求解(1)(2)(3)即可.
【详解】(1),而,
所以有
(2);
(3),而,
所以有.
32.(2022·全国·高一单元测试)解下列问题:
(1)若不等式的解集为,求a,b的值;
(2)若,求的最小值;
(3)已知,求代数式和的取值范围.
【答案】(1);(2)9;(3);
【分析】(1)由题意可得和3是方程的两个实根,则,从而可求出a,b的值;
(2)由已知可得,化简后利用基本不等式可求出其最小值,
(3)利用不等式的性质求解即可
【详解】(1)∵不等式的解集为
∴和3是方程的两个实根,
∴,解得
(2)∵,又
∴
当且仅当即时等号成立,
所以的最小值为9.
(3)∵,
∴
由,得,① .
由,得,② .
由①②得,
33.(2022·全国·高三专题练习)(1)已知,则取得最大值时的值为?
(2)已知,则的最大值为?
(3)函数 的最小值为?
【答案】(1);(2)1;(3)
【分析】(1)积的形式转化为和的形式,利用基本不等式求最值,并要检验等号成立的条件;
(2)结构为和的形式转化为积的形式,并使积为定值,同时要检验等号成立的条件;
(3)二次式除以一次式求最值,一般二次式用一次式表示出来,然后再分离,最后用基本不等式求解即可.
【详解】(1),
当且仅当,即时,取等号.
故所求的值为.
(2)因为,所以,
则.
当且仅当,即时,取等号.
故的最大值为1.
(3)
.
当且仅当,即时,取等号.
故函数的最小值为.
34.(2022·江苏连云港·高一期中)如图,某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形菜园.设菜园的长为xm,宽为ym.
(1)若菜园面积为72m2,则x,y为何值时,可使所用篱笆总长最小?
(2)若使用的篱笆总长度为30m,求的最小值.
【答案】(1)菜园的长x为12m,宽y为6m时,可使所用篱笆总长最小;(2).
【分析】(1)由已知可得xy=72,而篱笆总长为x+2y.利用基本不等式x+2y≥2即可得出;
(2)由已知得x+2y=30,利用基本不等式()•(x+2y)=55+2,进而得出.
【详解】(1)由已知可得xy=72,而篱笆总长为x+2y.又∵x+2y≥224,
当且仅当x=2y,即x=12,y=6时等号成立.
∴菜园的长x为12m,宽y为6m时,可使所用篱笆总长最小.
(2)由已知得x+2y=30,
又∵()•(x+2y)=55+29,
∴,当且仅当x=y,即x=10,y=10时等号成立.
∴的最小值是.
35.(2022·全国·高三专题练习)△ABC的内角A,B,C的对边分别为a,b,c,设.
(1)求B;
(2)若△ABC的面积等于,求△ABC的周长的最小值.
【答案】(1);(2).
【分析】(1)先利用边角互化将转化为关于B的方程,求出∠B.
(2)因为B已知,所以求面积的最小值即为求ac的最小值,结合余弦定理和基本不等式可以求得.
【详解】(1)因为,
由正弦定理得.
因为,所以sinA>0,所以,
所以,因为,
所以,即.
(2)依题意,即ac=4.
所以当且仅当时取等号.
又由余弦定理得
∴,当且仅当a=c=2时取等号.
所以△ABC的周长最小值为.
【点睛】本题主要考查解三角形、基本不等式求最值,考查学生逻辑推理、数学运算、直观想象的核心素养,是一道容易题.
36.(2022·陕西·长安一中高二阶段练习(文))已知在中,角,,的对边分别为,,,且.
(1)求的值;
(2)若,求面积的最大值.
【答案】(1);(2) .
【详解】分析:(1)在式子中运用正弦、余弦定理后可得.(2)由经三角变换可得,然后运用余弦定理可得,从而得到,故得.
详解:(1)由题意及正、余弦定理得,
整理得,
∴
(2)由题意得,
∴,
∵,
∴,
∴.
由余弦定理得,
∴,
,当且仅当时等号成立.
∴.
∴面积的最大值为.
点睛:(1)正、余弦定理经常与三角形的面积综合在一起考查,解题时要注意整体代换的应用,如余弦定理中常用的变形,这样自然地与三角形的面积公式结合在一起.
(2)运用基本不等式求最值时,要注意等号成立的条件,在解题中必须要注明.
新高考数学二轮复习分层练习专题03 不等式分层训练(含解析): 这是一份新高考数学二轮复习分层练习专题03 不等式分层训练(含解析),共25页。
新高考数学二轮复习培优讲义21 双曲线(含解析): 这是一份新高考数学二轮复习培优讲义21 双曲线(含解析),共38页。
新高考数学二轮复习培优讲义20 椭圆 (含解析): 这是一份新高考数学二轮复习培优讲义20 椭圆 (含解析),共35页。