









奥数六年级下册 第12讲:表面积与体积 课件+教案+作业
展开( 六年级 ) 备课教员:*** | ||||||||||||||||||
第十二讲 表面积与体积 | ||||||||||||||||||
一、教学目标:
| 知识目标 |
何体的表面积的计算方法; | ||||||||||||||||
能力目标 |
发展学生的空间观念。
关数学知识和方法的能力。 | |||||||||||||||||
情感目标 |
学习数学的兴趣。
数学的重要性。 | |||||||||||||||||
二、教学重点: | 进一步加深对相关体积单位实际大小的认识,发展学生的空间观念。 | |||||||||||||||||
三、教学难点: | 掌握常见几何体的表面积的计算方法; | |||||||||||||||||
四、教学准备: | PPT、长方形硬纸片、圆形纸片各一张 | |||||||||||||||||
五、教学过程: 第一课时(50分钟) 一、导入(5分) 【设计意图:通过实验观察,让学生深入地意识到体积基础公式是底面积×高,提高学生的空间想象力】 师:老师手中有两张纸片,看纸片上贴的是什么? 生:红包。 师:你们想要红包吗?每个红包里面的东西都不一样哦。 生:想要。 师:红包不是你们想要就能要。想获得红包就得经过老师的考验。这里2张长 方形的纸片,老师想看到一个圆柱体和一个长方体?哪位同学告诉老师怎 么办?上来操作给老师看看。 生:…… (长方形纸片快速地上下平移,我们可以看到一个长方体,圆形纸片水平的快速地上下平移我们可以看到一个圆柱体。) 师:这两位同学想象力非常棒,这两个红包就给这两位优秀的同学,看看里面 是什么? 生:…… 师:唉,老师再问问你们,拿着长方形这张纸上移,到这个点高度停止,它运 动的轨迹是不是这一段,就是它形成的长方体的高?圆形纸片呢? (不断地平移,加强学生的空间观念) 生:…… 师:不错,那这个形成的长方体和圆柱体底面积是不是就是纸片的面积? 生:是的。 师:好像立体图形和平面图形也是有些联系的哦,那我们进一步了解立体图形 的奥妙吧。 【探究新知,引入新课: 学生已经学习过了小学所有的立体图形,长方体、正方体、圆柱、圆锥,本堂主要是对该知识点进行整理和巩固,并应用到实际解决问题中】 【板书课题:表面积与体积】 | ||||||||||||||||||
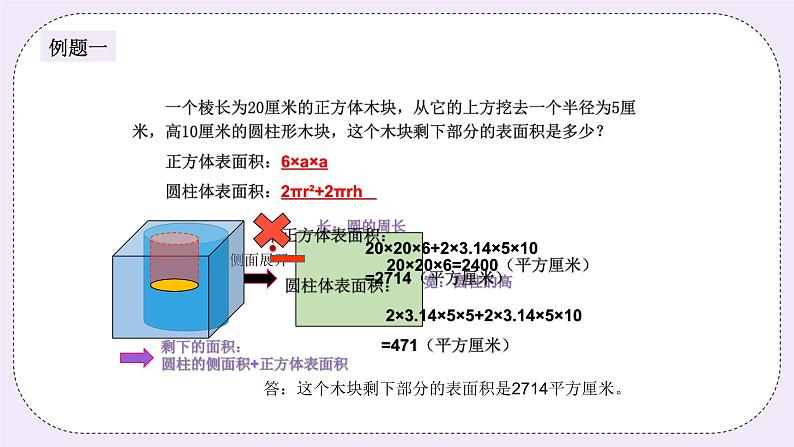
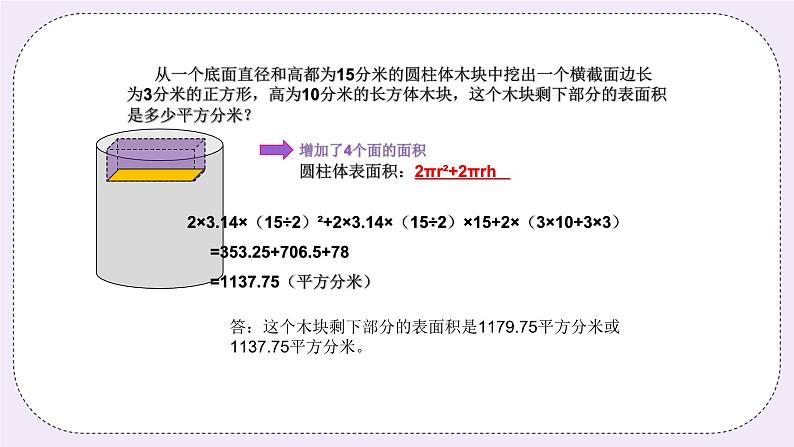
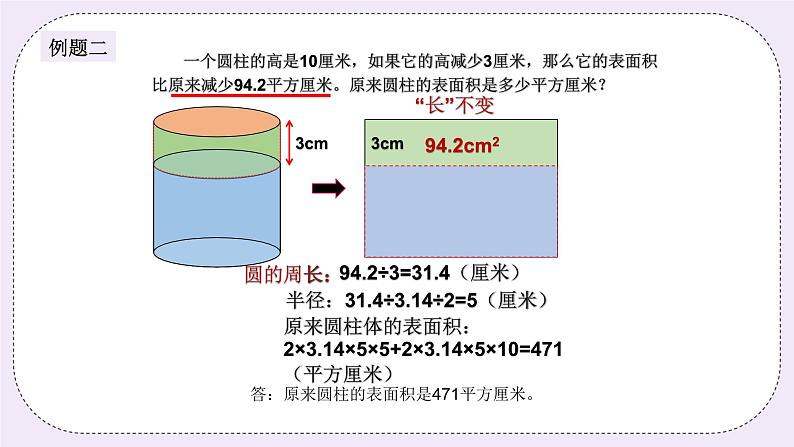
二、探索发现授课(40分) (一)例题1:(10分) 一个棱长为20厘米的正方体木块,从它的上方挖去一个半径为5厘米,高10厘米的圆柱形木块,这个木块剩下部分的表面积是多少? 讲解重点:回顾和整理正方体、圆柱体概念和表面积计算公式,及了解圆柱体表面积推导过程。 师:同学们,你们还记得什么是正方体吗?它有哪些特征呢? 生:…… 师:不错,正方体的6个面都是正方形,12棱长相等。那正方形的表面积计算 公式是什么呢? 生:棱长×棱长×6 师:那圆柱体的表面积怎么计算呢? 生:…… 师:它的侧面展开是什么图形? 生:…… 师:侧面展开图形的长是多少呢? 生:……板书: 正方体表面积:棱长×棱长×6;6×a×a 圆柱体表面积:2πr²+2πrh 师:不错,看来同学们都已经非常熟悉它们和它们的表面积计算公式了!在这 个题目中,一起来算算它们的表面积是多少?请2个同学把你的计算过程 写下来。 生:…… (同学板书的时候,老师下台巡视,了解同学们的知识掌握情况,并对基础稍差的同学进行指导) 板书: 正方体表面积:20×20×6=2400(平方厘米) 圆柱体表面积:2×3.14×5×5+2×3.14×5×10=471(平方厘米) 师:那木块剩下部分的表面积是正方体表面积减圆柱体表面积吗? (这里有学生会认为是,这里老师要展示PPT,让学生进一步仔细观察) 生:不是。 师:非常正确,那表面积是比原来多了还是少了? 师:多了哪一部分? 生:多了这个圆柱体的侧面积。 师:非常棒,看来同学们观察得很仔细,所以剩下的表面积就是 板书: 20×20×6+2×3.14×5×10=2714(平方厘米) 答:这个木块剩下部分的表面积是2714平方厘米。 练习1:(5分) 从一个底面直径和高都为15分米的圆柱体木块中挖出一个横截面边长为3分米的正方形,高为10分米的长方体木块,这个木块剩下部分的表面积是多少平方分米? 分析: 掌握长方体、圆柱体表面积计算,分析与剩下的表面积的关系,正确求解。 板书: 2×3.14×(15÷2)²+2×3.14×(15÷2)×15+4×3×10 =353.25+706.5+120 =1179.75(平方分米) 或:2×3.14×(15÷2)²+2×3.14×(15÷2)×15+2×(3×10+3×3) =353.25+706.5+78 =1137.75(平方分米) 答:这个木块剩下部分的表面积是1179.75平方分米或1137.75平方分米。 (二)例题2:(10分) 一个圆柱的高是10厘米,如果它的高减少3厘米,那么它的表面积比原来减少94.2平方厘米。原来圆柱的表面积是多少平方厘米? 讲解重点:侧面积展开图是个长方形,明白长不变,宽变化造成表面积的变化求出长,而这个长是底面圆的周长。 师:同学们,还记得例题中老师的提问,圆柱体的侧面展开图的长是什么? 生:底面圆的周长。 师:同学们的记性非常好哦!我们再来看看题目中,这里的高减少3厘米,实 际上是展开图长方形上的什么? 生:宽。 师:不错,长不变,宽减少3厘米,那么面积减少多少呢? (出示长方体高减少的动态图,通过观察让学生直观地感受到底面积是没有变化的,减少的是侧面积,而这是由展开图中宽减少造成的) 通过图中我们知道了面积减少了多少? 生:减少了94.2平方厘米。 师:不错,那么长是不是求出来了?长就是底面圆周长,所以半径就是…… 板书: 94.2÷3=31.4(厘米) 31.4÷3.14÷2=5(厘米) 师:半径知道了,高也是已知的,原来圆柱体的表面积,请一位同学来告诉老 师怎么列式? (点名刚才巡视掌握较弱的同学,答对后全班表扬,提高他学习数学的自信) 生:…… 师:非常棒,这位同学表现得很优秀,我们给他一个降龙十巴掌! 生:…… 板书: 94.2÷3=31.4(厘米) 31.4÷3.14÷2=5(厘米) 2×3.14×5×5+2×3.14×5×10=471(平方厘米) 答:原来圆柱的表面积是471平方厘米。 练习2:(5分) 一段长2米的圆柱体木料切成3段,表面积增加50.24平方厘米。原来这块木料的表面积是多少? 分析: 表面积增加的是底面圆的面积,总共增加了4个圆面积,求出圆面积,然后求出半径,原来木料的表面积就轻松求出来了,注意统一单位。 板书: 50.24÷4÷3.14÷2=2(厘米) 2×3.14×2×2+2×3.14×2×200=2537.12(平方厘米) 答:原来这块木料的表面积是2537.12平方厘米。 三、小结:(5分)
| ||||||||||||||||||
第二课时(50分) 一、复习导入(3分) 【设计意图:通过爱迪生的故事,让学生感受数学的魅力,体会水的柔性用于解决体积计算】 师:同学们,你们看我手里是什么? 生:…… 师:你们知道电灯泡是谁发明的吗? 生:…… 师:不错,是爱迪生发明的,他可是一位发明大王。那你们来看看这个电灯泡, 它是一个规则物体吗? (让学生近距离观察,注意安全) 生:…… 师:你们会计算它的体积吗? 生:不会。 师:虽然它有一定规则,但不是我们学过的立体图形,怎么办呢?我们来看看 大发明家爱迪生是怎么测量它的吧! (出示PPT) 师:这堂课,我们就来学习下爱迪生的方法吧! | ||||||||||||||||||
二、探索发现授课(42分) (一)例题3:(10分) 把一块棱长为12分米的正方体木料加工成一个体积最大的圆柱,这个圆柱体的体积是多少?加工成体积最大的圆锥体呢? 讲解重点:回顾和整理正方体和圆柱体的体积计算,掌握2种体积计算方法。 师:同学们,正方体、长方体、圆柱体、圆锥体体积的计算公式是什么? 生:…… 师:圆柱体、圆锥体体积的计算公式是什么? 板书: 正方体体积公式:棱长×棱长×棱长 长方体体积公式:长×宽×高 圆柱体体积公式:π×半径的平方×高 圆锥体体积公式:×π×半径的平方×高 师:看来这个难不倒聪明的同学们,那老师再问你们,还记得圆柱体体积的推 导过程吗? 生:…… 师:不错,能不能用一个公式统一表示长方体和圆柱体的体积计算方法? 生:可以,用底面积×高。 师:圆锥体的体积计算呢? 生:×底面积×高 板书: 正方体、长方体、圆柱体体积公式:底面积×高 圆锥体的体积公式:×底面积×高 师:非常棒,我们再来看看题目,正方体加工成最大的圆柱体,那么这个圆柱 体的直径是多少? 生:与正方体的棱长一样,是12分米。 师:这个圆柱体的高是多少? 生:就是正方体的高,12分米。 师:那么这个圆柱体的体积怎么列式? 生:3.14×(12÷2)²×12 师:那最大圆锥呢,它的底面积跟圆柱体的一个底面面积是不是一样? 生:是的。 师:高也是相同,所以它们是等底等高,等底等高圆锥体体积是圆柱体体积的 几分之几? 生: 师:非常棒,老师请一位乐于助人的同学上来替老师来书写下结果。 (老师下台巡视同学们都体积公式的掌握情况,并进行重点指导) 板书: 最大的圆柱体体积: 3.14×(12÷2)²×12=1356.48(立方分米) 最大的圆锥体积: ×3.14×(12÷2)²×12=452.16(立方分米) 答:最大的圆柱体体积是1356.48分米,圆锥是452.16立方分米。 练习3:(5分) 把一个底面周长为25.12厘米,高为40厘米的圆柱体铁块重新融化,铸成2个同样大小的高为80厘米的圆锥体铁块,这个圆锥体铁块的底面积有多大? 分析: 了解生活常识,融化后重铸的体积不变,再熟练地运用两个体积公式就可以轻松求解了。 板书: 25.12÷3.14÷2=4(厘米) 3.14×4×4×40÷2÷80×3=37.68(平方厘米) 答:这个圆锥体铁块的底面积有37.68平方厘米。 (二)例题4:(12分) 一个圆柱体木桶,从里面量,底面半径为2分米,里面装有4分米高的水,将一块打磨好的石块完全浸入水中,这时水上升了5厘米。问这个石块的体积是多少立方厘米? 讲解重点:体积计算在生活中的实际运用,了解水位法计算不规则物体的体积。 师:同学们,读完本题,来告诉老师,石块丢入水中,石块的体积和水的体积 有没有发生变化? 生:没有。 师:是的,它们的总体积是没有变化的,这时候石块完全浸入水中,它们总体 积的底面积是多少呢? 生:…… 师:唉,神奇的水好像让石块的底面积发生了改变,一起变成了同样的底面积。 我们妈妈的爱呢,也跟水一样,包容着一切。你们喜欢自己妈妈吗?平时 会帮妈妈做家务吗? 生:喜欢。 师:喜欢不是嘴巴上说说的哦,平时你们会帮妈妈做家务吗? 生:…… 师:老师为这些同学感到骄傲。来看看题目,那么现在底面积一样,它们的总 体积能求出来吗? 生:能。 师:老师请两位常常帮妈妈做家务的小能手来写下原来水的体积和后来的总体 积?是哪两位小朋友,答对了老师有奖励哦。 生:我、我…… 板书: 3.14×2×2×4 3.14×2×2×(4+5÷10) =50.24(立方分米) =56.52(立方分米) 师:这位同学非常仔细哦,解题没有忘记统一单位。那石块的体积是多少呢? 生:它们之间的差。 师:不错,其实就是它们水上升这部分的体积。快速地计算就是……老师喜欢 用厘米做单位,因为最后要我们求的是立方厘米。 生:…… 板书: 3.14×2×10×2×10×5 =6280(立方厘米) 答:石块的体积是6280立方厘米。 练习4:(5分) 一个底面积为36平方分米的长方体水箱,水深20厘米。竖直插入一根长1米,横截面为6平方分米的木料,木料底面与水箱底面接触,水未溢出。水面上涨了多少? 分析: 利用总体积不变的特点,用高=体积÷底面积,最后算出上涨的水面。注意统一单位。 板书: 36×20÷10÷(36-6)-20÷10=0.4(分米) 答:水面上升了0.4分米。 例题5:(选讲) 一只高是12厘米的圆柱体玻璃杯中水深6厘米,要在杯中放入一个底和杯的底面积相等,高6厘米圆锥体的铁块,水会不会溢出?如果不会溢出,这时水有多深? 讲解重点:进一步应用圆柱圆锥的体积公式,运用比的知识解决实际问题。 师:等底等高的圆柱体和圆锥体,它们体积的比是多少? 生:3:1。 师:不错,上堂课的同学们学习很认真哦。那老师再考考你们,等体积等高的 圆柱体和圆锥体,它们的底面积比是多少? 生:……(答错的学生再给他考时间,让学生独立完成思考) 师:不错,反了一下,是1:3。等体积等底面积,它们的高之比是多少? 生:也是1:3。 师:同学们都非常聪明,那我们来看下题目。 (出示PPT) 师:有水的部分高是6厘米,那么没水的部分高是多少呢? 师:不错,它的高和这个圆锥体高相等,底面积也相等。所以剩余部分的体积 还可以放下几个圆锥体铁块? 生:3个。 师:非常棒,所以说水没有溢出? 生:没有。 师:现在水高是6厘米,那么放入铁块后,水面一定高于6厘米。而圆锥铁块 的高也是6厘米,所以说铁块是完全浸没的。那么现在总体积是圆锥铁块 的多少? 生:4倍。 师:原来的体积呢? 生:3倍。 师:不错,它们底面积是相等的,体积的比是3:4,所以它们的高之比是多少? 生:3:4。 师:非常棒,同学们的联想能力太棒了。把降龙十巴掌送给自己。 板书: 6÷3×(1+3)=8(厘米) 答:这时水深8厘米。 练习5:(选做) 一个长宽高分别是25分米、24分米、10分米的长方体容器,水面高5分米。放进一个正方体铁块后,铁块顶面仍高于水面。这时水面高6分米。求正方体铁块的体积。 分析: 铁块顶面高于水面,说明铁块没有完全侵没,运用底面积=体积÷高,求出后来底面积,前后底面积之差就是正方体的底面积,分解质因数就能求出正方体的棱长。 板书: 25×24-25×24×5÷6=100(平方分米) 100=10×10 10×10×10=1000(立方分米) 答:正方体铁块的体积是1000立方分米。 三、总结:(5分) 1. 掌握小学阶段学习的立体图形的表面积和体积计算。 2. 熟练地运用公式体积=底面积×高,解决生活实际问题。 四、随堂练习:
多少平方厘米? 板书: r=15.7÷3.14÷2=2.5(厘米) S=2×3.14×2.5×2.5+2×3.14×2.5×15.7=285.74(平方厘米) 答:这个圆柱的表面积是285.74平方厘米。
的体积是24立方厘米,第二个圆柱的的体积比第一个圆柱多多少立方厘米? 板书: 24÷-24=18(立方厘米) 答:第二个圆柱的体积比第一个圆柱多18立方厘米。 3. 求下面图形的侧面积和体积。(单位:cm)
板书: V=3.14×(3÷2)2×6-3.14×(3÷2)2×(6-4)÷2=35.325(立方厘米) S=3.14×3×6-3.14×3×(6-4)÷2=47.1(平方厘米) 答:图形的侧面积是47.1平方厘米,体积是35.325立方厘米。
锥的体积分别是多少? 板书: 6×6×6÷(1+3)=54(立方分米) 54×3=162(立方分米) 答:圆柱的体积是162立方分米,圆锥的是54立方分米。
平方厘米,原来圆柱的体积是多少立方厘米? 板书: 25.12÷2=12.56(平方厘米) 12.56×8=100.48(立方厘米) 答:原来的圆柱的体积是100.48立方厘米。
| ||||||||||||||||||
奥数六年级下册 第10讲:常见的量 课件+教案+作业: 这是一份奥数六年级下册 第10讲:常见的量 课件+教案+作业,文件包含奥数六年级下册第10讲常见的量课件pptx、奥数六年级下册第10讲常见的量教案doc、奥数六年级下册第10讲常见的量作业docx等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
奥数六年级下册 第9讲:数的计算(二) 课件+教案+作业: 这是一份奥数六年级下册 第9讲:数的计算(二) 课件+教案+作业,文件包含奥数六年级下册第9讲数的计算二课件pptx、奥数六年级下册第9讲数的计算二教案doc、奥数六年级下册第9讲数的计算二作业docx等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
奥数六年级下册 第8讲:数的计算(一) 课件+教案+作业: 这是一份奥数六年级下册 第8讲:数的计算(一) 课件+教案+作业,文件包含奥数六年级下册第8讲数的计算一课件pptx、奥数六年级下册第8讲数的计算一教案doc、奥数六年级下册第8讲数的计算一作业docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













