九年级上册数学第22章 二次函数专题03 二次函数与销售利润问题

这是一份九年级上册数学第22章 二次函数专题03 二次函数与销售利润问题，文件包含专题03二次函数与销售利润问题原卷版docx、专题03二次函数与销售利润问题解析版docx等2份试卷配套教学资源，其中试卷共45页， 欢迎下载使用。

专题03 二次函数与销售利润问题
解题点拨
知识要点1：二次函数（）最大值求法
配方法：

当时，取最大值。
代入法：
当时，取最大值。（把带入求出最大值）
公式法：
借助顶点坐标公式带入求出最大值.
直击中考
1．（2022·河南郑州·统考一模）春节即将到来，某水果店进了一些水果，在进货单上可以看到：每次进货价格没有变化，第一次进货苹果400千克和梨500千克，共支付货款6200元；第二次进货苹果600千克和梨200千克，共支付货款6000元；为了促销，该店推出一款水果礼盒，内有3千克苹果和2千克梨，包装盒每个4元．市场调查发现：该礼盒的售价是70元时，每天可以销售80盒；每涨价1元，每天少销售2盒．
(1)求每个水果礼盒的成本（成本水果成本盒子成本）；
(2)若每个礼盒的售价是元是整数），每天的利润是元，求关于的函数解析式（不需要写出自变量的取值范围）；
(3)若每个礼盒的售价不超过元是大于70的常数，且是整数），直接写出每天的最大利润．
【答案】(1)40元
(2)
(3)当时，每天的最大利润为2450元；当时，每天的最大利润为

【分析】（1）设苹果进货价格为元千克，梨进货价格为元千克，根据题意列出方程组可求出和的值，进而得出结论；
（2）根据（售价成本）数量可得结论；
（3）根据二次函数的性质可直接得出结论．
【详解】（1）解：设苹果进货价格为元千克，梨进货价格为元千克，
依题意可列方程组：，
解得，，
苹果进货价格为8元千克，梨进货价格为6元千克
每个礼盒的成本为：（元）．
（2）解：．
（3）解：由（2）知，，
当时，每个礼盒取75元时，每天能够获得最大利润，且最大利润为2450元；
∵当时，w随m的增大而增大，
∴当时，每个礼盒的售价取 m 元时，每天的最大利润为．
【点睛】本题主要考查二次函数的应用，涉及二元一次方程组的应用，二次函数的性质等知识，关键是根据题意得出相关函数式．
2．（2022·江苏淮安·统考中考真题）端午节前夕，某超市从厂家分两次购进、两种品牌的粽子，两次进货时，两种品牌粽子的进价不变．第一次购进品牌粽子100袋和品牌粽子150袋，总费用为7000元；第二次购进品牌粽子180袋和品牌粽子120袋，总费用为8100元．
(1)求、两种品牌粽子每袋的进价各是多少元；
(2)当品牌粽子销售价为每袋54元时，每天可售出20袋，为了促销，该超市决定对品牌粽子进行降价销售．经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋．当品牌粽子每袋的销售价降低多少元时，每天售出品牌粽子所获得的利润最大？最大利润是多少元？
【答案】(1)种品牌粽子每袋的进价是25元，种品牌粽子每袋的进价是30元
(2)当品牌粽子每袋的销售价降低10元时，每天售出品牌粽子所获得的利润最大，最大利润是980元

【分析】（1）根据已知数量关系列二元一次方程组，即可求解；
（2）设品牌粽子每袋的销售价降低元，利润为元，列出关于的函数关系式，求出函数的最值即可．
【详解】（1）解：设种品牌粽子每袋的进价是元，种品牌粽子每袋的进价是元，
根据题意得，，
解得，
故种品牌粽子每袋的进价是25元，种品牌粽子每袋的进价是30元；
（2）解：设品牌粽子每袋的销售价降低元，利润为元，
根据题意得，
，
∵，
∴当品牌粽子每袋的销售价降低10元时，每天售出品牌粽子所获得的利润最大，最大利润是980元．
【点睛】本题考查二次函数和二元一次方程的实际应用，根据已知数量关系列出函数解析式和二元一次方程组是解题的关键．
3．（2022·四川巴中·统考中考真题）端午节吃粽子是中华民族的传统习俗，市场上猪肉粽进价比豆沙粽进价每盒贵10元，一盒猪肉粽加两盒豆沙粽进价为100元．
(1)求每盒猪肉粽和豆沙粽的进价；
(2)在销售中，某商家发现当每盒猪肉粽售价为50元时，每天可售出100盒，若每盒售价提高1元，则每天少售出2盒．设每盒猪肉粽售价为元，销售猪肉粽的利润为元，求该商家每天销售猪肉粽获得的最大利润．
【答案】(1)每盒猪肉粽的进价为40元，每盒豆沙粽进价为30元
(2)1800元

【分析】（1）设每盒猪肉粽的进价为元，每盒豆沙粽的进价为元，根据猪肉粽进价比豆沙粽进价每盒贵10元，一盒猪肉粽加两盒豆沙粽进价为100元列出方程组，解出即可．
（2）根据当时，每天可售出100盒，每盒猪肉粽售价为a元时，每天可售出猪肉粽盒，列出二次函数关系式，再化成顶点式即可得解．
（1）
设每盒猪肉粽的进价为元，每盒豆沙粽的进价为元，由题意得：

解得：
每盒猪肉粽的进价为40元，每盒豆沙粽进价为30元．
（2）

．
当时，w最大值为1800元．
∴该商家每天销售猪肉粽获得的最大利润为1800元．
【点睛】本题主要考查了二元一次方程组的实际应用以及二次函数的实际应用，根据题意列出相应的函数关系式是解此题的关键．
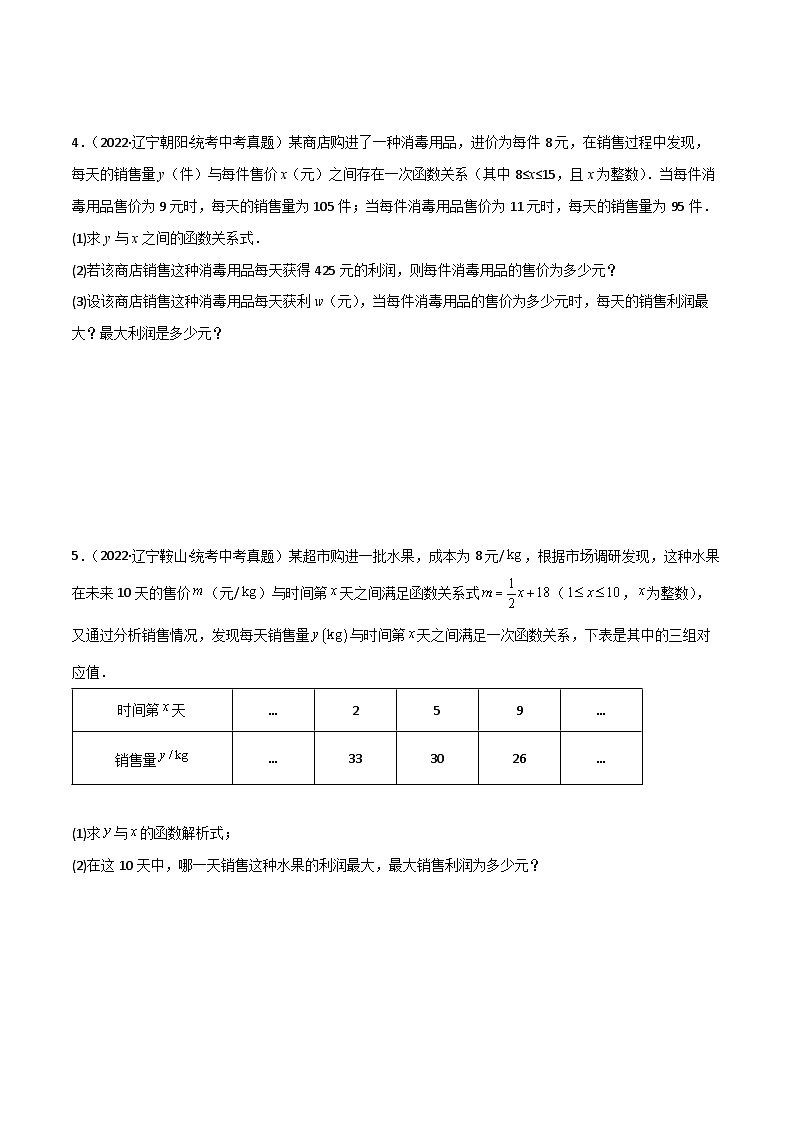
4．（2022·辽宁朝阳·统考中考真题）某商店购进了一种消毒用品，进价为每件8元，在销售过程中发现，每天的销售量y（件）与每件售价x（元）之间存在一次函数关系（其中8≤x≤15，且x为整数）．当每件消毒用品售价为9元时，每天的销售量为105件；当每件消毒用品售价为11元时，每天的销售量为95件．
(1)求y与x之间的函数关系式．
(2)若该商店销售这种消毒用品每天获得425元的利润，则每件消毒用品的售价为多少元？
(3)设该商店销售这种消毒用品每天获利w（元），当每件消毒用品的售价为多少元时，每天的销售利润最大？最大利润是多少元？
【答案】(1)
(2)13
(3)每件消毒用品的售价为15元时，每天的销售利润最大，最大利润是525元．

【分析】（1）根据给定的数据，利用待定系数法即可求出y与x之间的函数关系式；
（2）根据每件的销售利润×每天的销售量=425，解一元二次方程即可；
（3）利用销售该消毒用品每天的销售利润=每件的销售利润×每天的销售量，即可得出w关于x的函数关系式，再利用二次函数的性质即可解决最值问题．
【详解】（1）解：设y与x之间的函数关系式为，根据题意得：
，解得：，
∴y与x之间的函数关系式为；
（2）解：（-5x+150）（x-8）=425，
整理得：，
解得：，
∵8≤x≤15，
∴若该商店销售这种消毒用品每天获得425元的利润，则每件消毒用品的售价为13元；
（3）解：根据题意得：


∵8≤x≤15，且x为整数，
当x<19时，w随x的增大而增大，
∴当x=15时，w有最大值，最大值为525．
答：每件消毒用品的售价为15元时，每天的销售利润最大，最大利润是525元．
【点睛】本题考查了待定系数法求一次函数解析式以及二次函数的应用，解题的关键是找准题目的等量关系，
5．（2022·辽宁鞍山·统考中考真题）某超市购进一批水果，成本为8元/，根据市场调研发现，这种水果在未来10天的售价（元/）与时间第天之间满足函数关系式（，为整数），又通过分析销售情况，发现每天销售量与时间第天之间满足一次函数关系，下表是其中的三组对应值．
时间第天
…
2
5
9
…
销售量
…
33
30
26
…

(1)求与的函数解析式；
(2)在这10天中，哪一天销售这种水果的利润最大，最大销售利润为多少元？
【答案】(1)y＝−x＋35（1≤x≤10，x为整数）；
(2)在这10天中，第7天和第8天销售这种水果的利润最大，最大销售利润为378元．

【分析】（1）利用待定系数法求解即可；
（2）设销售这种水果的日利润为w元，得出w＝＝，，再结合1≤x≤10，x为整数，利用二次函数的性质可得答案．
【详解】（1）解：设每天销售量y与时间第x天之间满足的一次函数关系式为y＝kx＋b，
根据题意，得：，
解得，
∴y＝−x＋35（1≤x≤10，x为整数）；
（2）解：设销售这种水果的日利润为w元，
则w＝
＝
＝，
∵1≤x≤10，x为整数，
∴当x＝7或x＝8时，w取得最大值，最大值为378，
答：在这10天中，第7天和第8天销售这种水果的利润最大，最大销售利润为378元．
【点睛】本题主要考查了二次函数在销售问题中的应用，理清题中的数量关系并熟练掌握二次函数的性质是解题的关键．
6．（2022·湖北荆门·统考中考真题）某商场销售一种进价为30元/个的商品，当销售价格x（元/个）满足40＜x＜80时，其销售量y（万个）与x之间的关系式为y＝﹣x+9．同时销售过程中的其它开支为50万元．
(1)求出商场销售这种商品的净利润z（万元）与销售价格x函数解析式，销售价格x定为多少时净利润最大，最大净利润是多少？
(2)若净利润预期不低于17．5万元，试求出销售价格x的取值范围；若还需考虑销售量尽可能大，销售价格x应定为多少元？
【答案】(1)z＝﹣+12x﹣320，当x＝60时，z最大，最大利润为40
(2)45≤x≤75，x＝45时，销售量最大

【分析】（1）根据总利润＝单价利润×销量﹣40，可得 z 与x的函数解析式，再求出时，z最大，代入即可．
（2）当 z =17.5时，解方程得出x的值，再根据函数的增减性和开口方向得出 x的范围，结合 y 与 x的函数关系式，从而解决问题．
（1）
由题可知：
z＝y（x﹣30）﹣50
＝（﹣）（x﹣30）﹣50
＝﹣+12x﹣320，
∴当时，z最大，
∴最大利润为：﹣＝40；
（2）
当z＝17.5时，17.5＝﹣+12x﹣320，
∴x1＝45，x2＝75，
∵净利润预期不低于17.5万元，且a＜0，
∴45≤x≤75，
∵y＝﹣x+9．y随x的增大而减小，
∴x＝45时，销售量最大．
【点睛】本题主要考查了二次函数的实际应用，二次函数的性质，一次函数的性质等知识，正确列出 z 关于x的函数的解析式是解题的关键．
7．（2022·广东佛山·校考三模）某精品店购进甲、乙两种商品，已知购进件甲商品和件乙商品共需元，购进件甲商品与件乙商品共需元．
(1)求甲商品的和乙商品的进价．
(2)甲商品售价是元一件，可售出件，据商家统计，甲商品每涨价元，其销售量就减少件，请问售价定为多少时，才能使利润最大，并求出最大利润．
【答案】(1)甲、乙两种商品进价分别为元/件，元/件
(2)甲商品售价为元/件时，获得利润最大，最大利润为元

【分析】对于（1），根据2件甲商品的价格+1件乙商品的价格=36，3件甲商品的价格+2件乙商品的价格=64，列出方程组，再求出解即可；
对于（2），根据总利润=单件利润×销售量列出二次函数关系式，再根据二次函数图像的性质讨论极值得出答案．
【详解】（1）设甲、乙两种商品进价分别为元件，元件，
根据题意得，
解得，
答：甲、乙两种商品进价分别为元件，元件；
（2）设甲商品售价为元件，利润为元，
由题意得，，
，
当时，的值最大，
即甲商品售价为元件时，获得利润最大，最大利润为元．
【点睛】本题主要考查了二元一次方程组的应用，二次函数讨论极值的问题等，确定等量关系是解题的关键．
8．（2022·内蒙古鄂尔多斯·统考中考真题）某超市采购了两批同样的冰墩墩挂件，第一批花了6600元，第二批花了8000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进50个．
(1)求第二批每个挂件的进价；
(2)两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？
【答案】(1)第二批每个挂件的进价为40元
(2)当每个挂件售价定为58元时，每周可获得最大利润，最大利润是1080元

【分析】（1）设第二批每个挂件的进价为x元，则第一批每个挂件的进价为1.1x元，根据题意列出方程，求解即可；
（2）设每个售价定为y元，每周所获利润为w元，则可列出w关于y的函数关系式，再根据“每周最多能卖90个”得出y的取值范围，根据二次函数的性质可得出结论．
【详解】（1）设第二批每个挂件的进价为x元，则第一批每个挂件的进价为1.1x元，
根据题意可得，
，
解得x＝40．
经检验，x＝40是原分式方程的解，且符合实际意义，
∴1.1x＝44．
∴第二批每个挂件的进价为40元．
（2）设每个售价定为y元，每周所获利润为w元，
根据题意可知，w＝（y﹣40）[40+10（60﹣y）]＝﹣10+1440，
∵﹣10＞0，
∴当x≥52时，y随x的增大而减小，
∵40+10（60﹣y）≤90，
∴y≥55，
∴当y＝55时，w取最大，此时w＝﹣10+1440＝1350．
∴当每个挂件售价定为55元时，每周可获得最大利润，最大利润是1350元．
【点睛】本题综合考查分式方程和二次函数的应用，根据题意列出函数关系式是解题关键．
9．（2022·辽宁锦州·中考真题）某商场新进一批拼装玩具，进价为每个10元，在销售过程中发现．，日销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系．

(1)求y与x的函数关系式（不要求写出自变量x的取值范围）；
(2)若该玩具某天的销售利润是600元，则当天玩具的销售单价是多少元？
(3)设该玩具日销售利润为w元，当玩具的销售单价定为多少元时，日销售利润最大？最大利润是多少元？
【答案】(1)；
(2)40元或20元；
(3)当玩具的销售单价定为30元时，日销售利润最大；最大利润是800元；

【分析】（1）直接由待定系数法，即可求出一次函数的解析式；
（2）根据题意，设当天玩具的销售单价是元，然后列出一元二次方程，解方程即可求出答案；
（3）根据题意，列出w与的关系式，然后利用二次函数的性质，即可求出答案．
【详解】（1）解：由图可知，设一次函数的解析式为，
把点（25，50）和点（35，30）代入，得
，解得，
∴一次函数的解析式为；
（2）解：根据题意，设当天玩具的销售单价是元，则
，
解得：，，
∴当天玩具的销售单价是40元或20元；
（3）解：根据题意，则
，
整理得：；
∵，
∴当时，有最大值，最大值为800；
∴当玩具的销售单价定为30元时，日销售利润最大；最大利润是800元．
【点睛】本题考查了二次函数的性质，二次函数的最值，一次函数的应用，解一元二次方程，解题的关键是熟练掌握题意，正确的找出题目的关系，从而进行解题．
10．（2022·辽宁盘锦·中考真题）精准扶贫工作已经进入攻坚阶段，贫苦户李大叔在政府的帮助下，建起塑料大棚，种植优质草莓，今年二月份正式上市销售．在30天的试销中，每天的销售量与销售天数x满足一次函数关系，部分数据如下表：
x（天）
1
2
3
…
x
每天的销售量（千克）
10
12
14
…
      

设第x天的售价为y元/千克，y关于x的函数关系满足如下图像：已知种植销售草莓的成本为5元/千克，每天的利润是w元．（利润＝销售收入﹣成本）

(1)将表格中的最后一列补充完整；
(2)求y关于x的函数关系式；
(3)求销售草莓的第几天时，当天的利润最大？最大利润是多少元？
【答案】(1)见解析
(2)y＝
(3)销售草莓的第30天时，当天的利润最大，最大利润是272元

【分析】（1）设每天的销售量为z，则用待定系数法可求出每天的销售量与销售天数x的一次函数关系式，根据关系式填表即可；
（2）根据图像写出分段函数即可；
（3）根据函数关系列出x和w之间的关系式，利用二次函数的性质求最值即可．
【详解】（1）设每天的销量为z，
∵每天的销售量与销售天数x满足一次函数关系，
∴z＝sx+t，
∵当x＝1时，z＝10，x＝2时z＝12，
∴，
解得，
即z＝2x+8，
当时，销售量，
则将表格中的最后一列补充完整如下表：
x（天）
1
2
3
…
30
每天的销售量（千克）
10
12
14
…
68

（2）由函数图像知，当0＜x≤20时，y与x成一次函数，且函数图像过(10，14)，(20，9)，
设y＝kx+b，
∴，
解得，
∴y＝-x+19（0＜x≤20），
当20＜x≤30时，y＝9，
∴y关于x的函数关系式为y＝；
（3）由题意知，当0＜x≤20时，
w＝＝﹣x2+24x+112＝，
∴此时当x＝12时，w有最大值为256，
当20＜x≤30时，
w＝（2x+8）×（9-5）＝18x+32，
∴此时当x＝30时，w有最大值为272，
综上所述，销售草莓的第30天时，当天的利润最大，最大利润是272元．
【点睛】本题主要考查一次函数的图像和性质，二次函数的应用等知识，熟练掌握一次函数的图像和性质及二次函数的应用是解题的关键．
11．（2022·山东青岛·统考中考真题）李大爷每天到批发市场购进某种水果进行销售，这种水果每箱10千克，批发商规定：整箱购买，一箱起售，每人一天购买不超过10箱；当购买1箱时，批发价为8.2元/千克，每多购买1箱，批发价每千克降低0.2元．根据李大爷的销售经验，这种水果售价为12元/千克时，每天可销售1箱；售价每千克降低0.5元，每天可多销售1箱．
(1)请求出这种水果批发价y（元/千克）与购进数量x（箱）之间的函数关系式；
(2)若每天购进的这种水果需当天全部售完，请你计算，李大爷每天应购进这种水果多少箱，才能使每天所获利润最大？最大利润是多少？
【答案】(1)且x为整数．
(2)李大爷每天应购进这种水果7箱，获得的利润最大，最大利润是140元．

【分析】（1）根据题意列出，得到结果．
（2）根据销售利润=销售量（售价-进价），利用（1）结果，列出销售利润w与x的函数关系式，即可求出最大利润．
【详解】（1）解：由题意得

∴批发价y与购进数量x之间的函数关系式是，且x为整数．
（2）解：设李大爷销售这种水果每天获得的利润为w元
则


∵
∴抛物线开口向下
∵对称轴是直线
∴当时，w的值随x值的增大而增大
∵x为正整数，∴此时，当时，
当时，w的值随x值的增大而减小
∵x为正整数，∴此时，当时，
∵
∴李大爷每天应购进这种水果7箱，获得的利润最大，最大利润是140元．
【点睛】本题考查了二次函数的性质在实际生活中的应用，最大销售利润的问题常利用二次函数的增减性来解答，解题关键是理解题意，确定变量，建立函数模型，然后结合实际选择最优方案进行解决．
12．（2022·广西贺州·统考中考真题）2022年在中国举办的冬奥会和残奥会令世界瞩目，冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓，成为热销产品，某商家以每套34元的价格购进一批冰墩墩和雪容融套件，若该产品每套的售价是48元时，每天可售出200套；若每套售价提高2元，则每天少卖4套．
(1)设冰墩墩和雪容融套件每套售价定为x元时，求该商品销售量y与x之间的函数关系式；
(2)求每套售价定为多少元时，每天销售套件所获利润W最大，最大利润是多少元？
【答案】(1)；
(2)每套售价为91元时，每天销售套件所获利润最大，最大利润是6498元．

【分析】（1）根据 “该产品每套的售价是48元时，每天可售出200套；若每套售价提高2元，则每天少卖4套．”列出函数关系式，即可求解；
（2）根据利润等于每件的利润乘以销售量，可得到函数关系式，再利用二次函数的性质，即可求解．
【详解】（1）解：根据题意，得

与x之间的函数关系式是．
（2）解：根据题意，得


∴抛物线开口向下，W有最大值
当时，
答：每套售价为91元时，每天销售套件所获利润最大，最大利润是6498元．
【点睛】本题主要考查了一次函数的应用，二次函数的实际应用，明确题意，准确得到等量关系是解题的关键．
13．（2022·广西·统考中考真题）打油茶是广西少数民族特有的一种民俗，某特产公司近期销售一种盒装油茶，每盒的成本价为50元，经市场调研发现，该种油茶的月销售量y（盒）与销售单价x（元）之间的函数图像如图所示．

(1)求y与x的函数解析式，并写出自变量x的取值范围；
(2)当销售单价定为多少元时，该种油茶的月销售利润最大?求出最大利润．
【答案】(1)y= -5x+500，50＜x＜100
(2)75元，3125元

【分析】（1）设直线的解析式为y=kx+b，根据题意，得，确定解析式，结合图像，确定自变量取值范围是50＜x＜100．
（2）设销售单价为x元，总利润为w元，根据题意构造二次函数，根据函数的最值计算即可．
【详解】（1）设直线的解析式为y=kx+b，根据题意，得
，
解得
∴ 函数的解析式为y= -5x+500，
当y=0时，-5x+500=0，
解得x=100，
结合图像，自变量取值范围是50＜x＜100．
（2）设销售单价为x元，总利润为w元，根据题意，得：
W=（x-50）(-5x+500)
=，
∵-5＜0，
∴ w有最大值，且当x=75时，w有最大值，为3125，
故销售单价定为75元时，该种油茶的月销售利润最大；最大利润是3125元．
【点睛】本题考查了待定系数法确定一次函数的解析式，构造二次函数求最值，熟练掌握待定系数法，正确构造二次函数是解题的关键．
14．（2022·湖北十堰·统考中考真题）某商户购进一批童装，40天销售完毕．根据所记录的数据发现，日销售量（件）与销售时间（天）之间的关系式是 ，销售单价（元/件）与销售时间（天）之间的函数关系如图所示．

(1)第15天的日销售量为_________件；
(2)当时，求日销售额的最大值；
(3)在销售过程中，若日销售量不低于48件的时间段为“火热销售期”，则“火热销售期”共有多少天？
【答案】(1)30
(2)2100元
(3)9天

【分析】（1）将直接代入表达式即可求出销售量；
（2）设销售额为元，分类讨论，当时，由图可知，销售单价；当时，有图可知，p是x的一次函数，用待定系数法求出p的表达式；分别列出函数表达式，在自变量取值范围内求取最大值即可；
（3）分类讨论，当和时列出不等式，解不等式，即可得出结果．
【详解】（1）解：当时，销售量；
故答案为30；
（2）设销售额为元，
①当时，由图可知，销售单价，
此时销售额
∵，
∴随的增大而增大
当时，取最大值
此时
②当时，有图可知，p是x的一次函数，且过点（20，40）、（40，30）
设销售单价，
将（20，40）、（40，30）代入得：
解得
∴
∴
∵，
∴当时，随的增大而增大
当时，取最大值
此时
∵
∴的最大值为2100，
∴当时，日销售额的最大值为2100元；
（3）当时，
解得
∴
当，
解得
∴
∴，共9天
∴日销售量不低于48件的时间段有9天．
【点睛】本题考查一元一次方程、一次函数、一元一次不等式、二次函数，是初中数学应用题的综合题型，解题的关键在于利用题目中的等量关系、不等关系列出方程、不等式，求出函数表达式，其中自变量取值范围是易错点、难点．
15．（2022·浙江金华·统考中考真题）“八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量（吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为，部分对应值如表：
售价x（元/千克）
…
2.5
3
3.5
4
…
需求量（吨）
…
7.75
7.2
6.55
5.8
…

②该蔬菜供给量（吨）关于售价x（元/千克）的函数表达式为，函数图象见图1．
③1~7月份该蔬菜售价（元/千克），成本（元/千克）关于月份t的函数表达式分别为，，函数图象见图2．

请解答下列问题：
(1)求a，c的值．
(2)根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．
(3)求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．
【答案】(1)
(2)在4月份出售这种蔬菜每千克获利最大，见解析
(3)该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元

【分析】（1）运用待定系数法求解即可；
（2）设这种蔬菜每千克获利w元，根据列出函数关系式，由二次函数的性质可得结论；
（3）根据题意列出方程，求出x的值，再求出总利润即可．
（1）
把，代入可得

②-①，得，
解得，
把代入①，得，
∴．
（2）
设这种蔬菜每千克获利w元，根据题意，
有，
化简，得，
∵在的范围内，
∴当时，w有最大值．
答：在4月份出售这种蔬菜每千克获利最大．
（3）
由，得，
化简，得，解得（舍去），
∴售价为5元/千克．
此时，（吨）（千克），
把代入，得，
把代入，得，
∴总利润（元）．
答：该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元．
【点睛】此题主要考查了函数的综合应用，结合函数图象得出各点的坐标，再利用待定系数法求出函数解析式是解题的关键．
16．（2022·浙江温州·温州市第三中学校考模拟预测）某商店决定购进，两种“冰墩墩”纪念品进行销售．已知每件种纪念品比每件种纪念品的进价高30元．用1000元购进种纪念品的数量和用400元购进种纪念品的数量相同．
(1)求，两种纪念品每件的进价分别是多少元？
(2)该商场通过市场调查，整理出型纪念品的售价与数量的关系如下表，
售价（元/件）


销售量（件）
100


①当为何值时，售出纪念品所获利润最大，最大利润为多少？
②该商场购进，型纪念品共200件，其中型纪念品的件数小于型纪念品的件数，但不小于50件．若型纪念品的售价为元/件时，商场将，型纪念品均全部售出后获得的最大利润为2800元，求的值．
【答案】(1)，两种纪念品每件的进价分别是元和元
(2)①当时，售出纪念品所获利润最大，最大利润为元；②

【分析】（1）设纪念品每件的进价是元，则纪念品每件的进价是元，根据用1000元购进种纪念品的数量和用400元购进种纪念品的数量相同，列出分式方程，进行求解即可；
（2）①设利润为，根据图表，利用总利润等于单件利润乘以销售数量，列出函数关系式，根据函数的性质，求出最值即可；②设该商场购进型纪念品件，则购进型纪念品件，根据题意列出不等式组，求出的取值范围，进而得到型纪念品的最大利润，设总利润为，求出函数关系式，根据函数的性质，求出当时，的值即可．
【详解】（1）解：设纪念品每件的进价是元，则纪念品每件的进价是元，由题意，得：，
解得：，
经检验：是原方程的解；
当时：；
∴，两种纪念品每件的进价分别是元和元；
（2）解：①设利润为，由表格，得：
当时，，
∵，
∴随着的增大而增大，
∴当售价为：元时，利润最大为：元；
当，，
∵，
∴当时，利润最大为：元；
综上：当时，售出纪念品所获利润最大，最大利润为元．
②设该商场购进型纪念品件，则购进型纪念品件，由题意，得：，
解得：，
由①可知：当型纪念品的售价为元时，售出型纪念品的利润最大；
设，型纪念品均全部售出后获得的总利润为：，
则：，
整理，得：，
∵，
∴，
∴随的增大而减小，
∴当时，有最大值，最大值为：，
∴．
【点睛】本题考查分式方程的应用，一次函数的应用，二次函数的应用．根据题意，正确的列出分式方程和函数表示式，利用函数的性质，求最值，是解题的关键．
17．（2022·山东滨州·模拟预测）重庆潼南某一蔬菜种植基地种植的一种蔬菜，它的成本是每千克元，售价是每千克元，年销量为万千克多吃绿色蔬菜有利于身体健康，因而绿色蔬菜倍受欢迎，十分畅销．为了获得更好的销量，保证人民的身体健康，基地准备拿出一定的资金作绿色开发，根据经验，若每年投入绿色开发的资金万元，该种蔬菜的年销量将是原年销量的倍，它们的关系如下表：
万元














(1)试估计并验证与之间的函数类型并求该函数的表达式；
(2)若把利润看着是销售总额减去成本费和绿色开发的投入资金，试求年利润万元与绿色开发投入的资金万元的函数关系式；并求投入的资金不低于万元，又不超过万元时，取多少时，年利润最大，求出最大利润．
(3)基地经调查：若增加种植人员的奖金，从而提高种植积极性，又可使销量增加，且增加的销量万千克与增加种植人员的奖金万元之间满足，若基地将投入万元用于绿色开发和提高种植人员的奖金，应怎样分配这笔资金才能使年利润达到万元且绿色开发投入大于奖金？
【答案】(1)
(2)时，最大为万元
(3)用于绿色开发的资金为万元，奖金为万元

【分析】根据题意判断出函数解析式的形式，再利用待定系数法求二次函数解析式，可求出与的二次函数关系式．
根据题意可知，利用顶点坐标公式解题即可；
将代入中的，故；再将代入，故，由于单位利润为，所以由增加奖金而增加的利润就是，进而求出总利润，即可得出答案．
【详解】（1）根据不是一次函数(不是线性的)，也不是反比例函数的值不是常数)，所以选择二次函数，
设与的函数关系式为，
由题意得：
，
解得：，
与的函数关系式为：；
（2）利润销售总额减去成本费和绿色开发的投入资金，
；
当时，最大，
由于投入的资金不低于万元，又不超过万元，所以，
而，抛物线开口向下，且取值范围在顶点右侧，随的增大而减小，故最大值在处，
当时，最大为：万元；
（3）设用于绿色开发的资金为万元，则用于提高奖金的资金为万元，
将代入中的，故；
将代入，故，
由于单位利润为，所以由增加奖金而增加的利润就是；
所以总利润，
因为要使年利润达到万，所以，
整理得，
解得：或，而绿色开发投入要大于奖金，
所以
所以用于绿色开发的资金为万元，奖金为万元．
【点睛】此题主要考查了二次函数的应用，以及待定系数法求二次函数解析式和一元二次方程的解法等知识，根据已知得出由增加奖金而增加的利润是解题关键．
18．（2022·辽宁大连·校考模拟预测）新冠肺炎疫情后期，我县某药店进了一批口罩，成本价为元/个，投入市场销售，其销售单价不低于成本，按物价局规定销售利润率不高于．经一段时间调查，发现每天销售量（个）与销售单价（元/个）之间存在一次函数关系，且有两天数据为：销售价定为元，每天销售个；销售价定为元，每天销售个．
(1)直接写出与之间的函数关系式，并写出自变量的取值范围．
(2)如果该药店销售口罩每天获得元的利润，那么这种口罩的销售单价应定为多少元？
(3)设每天的总利润为元，当销售单价定为多少元时，该药店每天的利润最大？最大利润是多少元？
【答案】(1)
(2)元
(3)元，元

【分析】（1）设与之间的函数关系式为，用待定系数法可得与之间的函数关系式为，根据销售单价不低于成本，按物价局规定销售利润率不高于80%，可得；
（2）根据题意得：，即可解得答案；
（3）由题意得：，整理计算，再利用二次函数的性质可得答案．
【详解】（1）设与之间的函数关系式为，将销售价定为元，每天销售个；销售价定为元，每天销售个代入得：
，解得，
与的函数关系式为，
销售单价不低于成本，按物价局规定销售利润率不高于，
，
解得，
；
（2）根据题意得：，
整理得：，
解得：，不合题意，舍去，
答：如果每天获得元的利润，销售单价应定为元；
（3）由题意得：



，
抛物线开口向下，有最大值，
时，最大值是，
答：销售单价定为元时，每天的利润最大，最大利润是元．
【点睛】本题考查一元二次方程及二次函数的应用，解题关键是读懂题意，找到等量关系列方程和函数关系是．
19．（2022·贵州遵义·三模）红星公司销售一种成本为4元/件的产品，若月销售单价不高于5元/件.一个月可售出5万件；月销售单价每涨价1元，月销售量就减少 万件.其中月销售单价不低于成本.设月销售单价为x（单位：元/件），月销售量为y（单位：万件）.
(1)直接写出y与x之间的函数关系式，并写出自变量x的取值范围；
(2)当月销售单价是多少元/件时，月销售利润最大，最大利润是多少万元？
(3)为响应国家“乡村振兴”政策，该公司决定在某月每销售件产品便向大别山区捐款a元，已知该公司捐款当月的月销售单价不高于70元/件，月销售最大利润是78万元，求a的值
【答案】(1)
(2)7元/件，最大利润为9万元
(3)

【分析】（1）分和两种情况，根据“月销售单价每涨价1元，月销售量就减少万件”即可得函数关系式，再根据求出的取值范围；
（2）在（1）的基础上，根据“月利润（月销售单价成本价）月销售量”建立函数关系式，分别利用一次函数和二次函数的性质求解即可得；
（3）设该产品的捐款当月的月销售利润为万元，先根据捐款当月的月销售单价、月销售最大利润可得，再根据“月利润（月销售单价成本价）月销售量”建立函数关系式，然后利用二次函数的性质即可得．
【详解】（1）解：由题意，当 时， ，
当 时， ，
，
，
解得 ，
综上，
（2）解：设该产品的月销售利润为 万元，
①当 时， ，
由一次函数的性质可知，在 内， 随 的增大而增大，
则当 时， 取得最大值，最大值为 ；
②当 时， ，
由二次函数的性质可知，当 时， 取得最大值，最大值为9，
因为 ，
所以当月销售单价是7元/件时，月销售利润最大，最大利润是9万元
（3）解： 捐款当月的月销售单价不高于7元/件，月销售最大利润是78万元（大于5万元），
，
设该产品捐款当月的月销售利润为 万元，
由题意得： ，
整理得： ，
，
在 内， 随 的增大而增大，
则当 时， 取得最大值，最大值为 ，
因此有 ，
解得
【点睛】本题考查了二次函数与一次函数的实际应用，正确建立函数关系式是解题关键．
20．（2022·四川成都·校考三模）为了稳增长，成都市政府开展了促线下消费活动，共发放约6亿元的“成都520”消费券．某商家参与了本次活动，售卖一款成本为30元/件的服装．经市场调研发现，这款服装的销售量y（单位：件）与销售价格x（单位：元/件）之间的关系如图所示．

(1)求y与x的函数关系式；
(2)为让利顾客，活动要求利润不得高于成本的80%．试问：商家售价定为多少时，总利润最大？并求出此时的最大利润．
【答案】(1)
(2)54元/件时，总利润最大，最大利润为2208元

【分析】（1）根据图形中数据用待定系数法求函数解析式即可；
（2）根据利润=单件利润×销售量列出函数解析式，再根据x的取值范围和二次函数的性质求最值即可．
【详解】（1）解：设销售量y（件）与售价x（元/件）之间的函数关系式为，
则，
解得：，
∴销售量y（件）与售价x（元/件）之间的函数关系式是；
（2）商家销售该服装的利润为w元，
根据题意得：，
∵活动要求利润不得高于成本的80%．
∴，
解得：，
∵，
∴当时，w有最大值，最大值为2208，
∴商家售价定为54元/件时，总利润最大，最大利润为2208元．
【点睛】本题考查一次函数的应用，二次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和二次函数的性质解答．
21．（2022·辽宁朝阳·模拟预测）商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施，经调查发现，每件商品每降价1元，商场每天可多售出2件，设每件商品降低x元据此规律，请回答：
(1)商场日销售量增加 件，每件商品盈利　　元（用含x的代数式表示）；
(2)在上述条件不变，销售正常的情况下，设商场日盈利y元，求y与x的函数关系式；
(3)在（2）的条件下，每件商品降价多少元时，商场日盈利最高？
【答案】(1)，；
(2)
(3)每件商品降价35元时，商场日盈利最高．

【分析】（1）每件商品每降价1元，商场平均每天可多售出2件．设每件商品降价x元. 商场日销售量增加件，每件商品盈利元；
（2）根据（1）得，单件利润乘以销售量等于利润，即可得到y与x的函数关系式；
（3）由题意得：利润函数的表达式为，再化为顶点式得，得，当时，y有最大值．
【详解】（1）解：每天销售30件，每件盈利50元，每件商品每降价1元，商场平均每天可多售出2件，
∴当降价x元时，商场日销售量增加件，每件商品盈利为元，
故答案为：，；
（2）解：根据题意得：．
（3）解：，
当时，y有最大值，
答：每件商品降价35元时，商场日盈利最高．
【点睛】本题考查二次函数的销售问题，涉及到利润函数=单件利润乘以销售数量，利用二次函数的性质求最值，通常都是化为顶点式来解决问题．
22．（2022·广东深圳·深圳市宝安中学（集团）校考三模）戴口罩、勤洗手、少聚会”是新冠肺炎疫情防控的有效措施．为保证防疫口罩供应，为满足市民防护需求，某药店想要购进A、B两种口罩，B型口罩的每盒进价是A型口罩的两倍少10元．用6000元购进A型口罩的盒数与用10000元购进B型口罩盒数相同．
(1)A，B型口罩每盒进价分别为多少元？
(2)经市场调查表明，B型口罩更受欢迎，当每盒B型口罩售价为60元时，日均销量为100盒，B型口罩每盒售价每增加5元，日均销量减少25盒．当B型口罩每盒售价多少元时，销售B型口罩所得日均总利润最大？最大日均总利润为多少元？
【答案】(1)A型口罩的每盒进价是30元，B型口罩每盒进价是50元
(2)当B型口罩每盒售价65元时，销售B型口罩所得日均总利润最大，最大日均总利润为1125元

【分析】（1）根据用6000元购进A型口罩的盒数与用10000元购进B型口罩盒数相同列方程计算即可；
（2）设售价为元，总利润为，根据题意求出函数解析式，再进行计算即可．
（1）
解：设A型口罩每盒进价为元，则：B型口罩每盒进价为元，
由题意得：，
解得：，
经检验：是原方程的解．
，
∴A型口罩的每盒进价是30元，B型口罩每盒进价是50元．
（2）
解：设B型口罩每盒售价为元，总利润为，
由题意得：，
整理的：，
∴当时，有最大值：1125．
答：当B型口罩每盒售价65元时，销售B型口罩所得日均总利润最大，最大日均总利润为1125元．
【点睛】本题考查分式方程和二次函数的应用．根据题意正确的列出方程和函数表达式是解题的关键．