








奥数六年级上册 第6讲:比的认识和应用 课件+教案
展开( 六年级 ) 备课教员:××× | |||
第六讲 比的认识和应用 | |||
一、教学目标: | 1. 理解比的意义,能正确读写,会求比值,理解比与除法、 分数的关系。 2. 能运用比的意义解决按照一定的比进行分配的实际问题。 | ||
二、教学重点: | 1. 理解按一定比例来分配一个数量的意义。 | ||
三、教学难点: | 1. 能够运用比的意义解决按照一定的比进行分配的实际问 题。 | ||
四、教学准备: | PPT | ||
五、教学过程: 第一课时(50分钟) 导入(5分) 师:秋天到了,橘子园里大丰收,果农给芭啦啦综合学校运来了一筐橘子,要 分给五年级、六年级两个班级,你觉得该怎样分呢? 生:五年级分得多,六年级分得多,一个班一半。 师:一个班一半,就是平均分,我们可以用比来表示,应该怎么表示呢? 生:1:1 师:两个班级还可以怎样分? 生:按人数分配,人多的班分多点,人少的班分少点。 师:六年级30人,五年级20人,按人数分配怎么分合理? (多提问几名学生,并说说他们的想法) 生:按照大班和小班的人数比3:2分。 (提供现实生活情境,使学生体会到数学与生活的联系,激发学生的学习兴趣,引导学生分析问题中的数学信息。) 师:这节课我们就来学习比的知识。 【板书课题:比的认识和应用】 | |||
二、探索发现授课(40分) (一)例题1:(13分) 化最简整数比。 25:375 1.5:25% :35%
求比值。 : 2.5:37.5% 100公顷:62500平方米
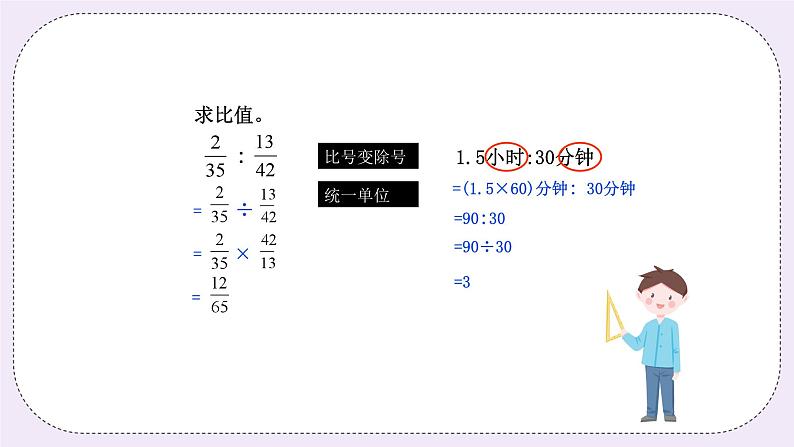
师:同学们,什么叫做最简整数比呢? 生:最简整数比指的是比的前项和后项都是整数,且这两个整数互质。 (朗读教材) 师:不错,那同学们还记得什么叫做互质吗? (复习互质的概念,两个整数的最大公约数是1称它们是互质的) 生:…… 师:我们来看第一题,25:375,比的前项是多少?比的后项?它们互质吗? (引导学生进一步掌握比的认识) 生:…… 师:25:375它们不是互质的,还可以进行化简,比的前项和后项同除以它们的 最大公约数。 板书: 25:375 =1:15 师:我们再来看看1.5:25%这题,我们怎么换算呢?以前我们遇到有百分数的计 算中常常把百分数转换成分数、小数计算。那么本题是否也可以呢? (引导学生回忆有百分数时的计算做法,过渡到化简整数比) 生:…… 师:把百分数转换成小数后,变成了1.5:0.25。接下来要把小数转换成整数, 我们该怎么做呢?想想比和分数、除法的比较? (引导学生运用比的基本性质转换成整数) 生:…… 师:把比的前项和后项同时扩大100倍,再进行化简。 板书: 1.5:25% =1.5:0.25 =150:25 =6:1 师:不错,看来同学们都已经掌握了求最简整数比的方法了,我们动手来试下 这题:35%吧。 (巡视看看学生的掌握能力,并根据情况在练习中进行关注) 板书: :35% =: =28:35 =4:5 师:同学们,什么是求比的比值呢? (引导学生对求比值的概念熟悉和应用) 生:…… 师:根据比的意义,用比的前项除以比的后项,最后用整数、小数或者分数表 示。比值是没有单位的,在有单位的比中求比值要统一单位。我们先来说 说:怎么求? (比号变除号,求出它们的商) 板书: : =÷ =× = 师:接下来这题2.5:37.5%同学们来动手试下吧。 生:…… 板书: 2.5:37.5% =2.5÷37.5% = 师:我们在求有单位的比值中我们先统一单位,1公顷等于多少平方米呢?1平 方千米等于多少公顷呢? (复习平方单位中公顷和平方米、平方千米的转换) 板书: 100公顷:62500平方米 =(100×10000)平方米:62500平方米 =16 师:比值是没有单位的,所以我们一定要注意最后书写不要带上单位。 练习1:(6分) 化最简整数比。 13:91 2.35:15% : 求比值。 : 1.5小时:30分钟 分析:熟悉掌握比的知识、化成最简整数比和求比值的方法。 板书: 化最简整数比。 13:91 2.35:15% : =1:7 =2.35:0.15 =(×15×17):(×15×17) =47:3 =68:225 求比值。 : 1.5小时:30分钟 =÷ =90分钟:30分钟 =× =90:30 = =3
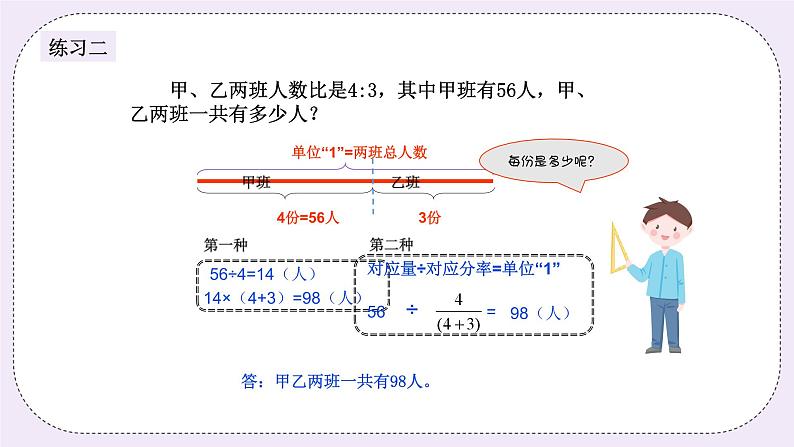
(二)例题2:(13分) 芭啦啦综合教育学校组织学生秋游,参加爬山和参加划船的人数之比是5:8,参加划船的人数是112人,秋游的总人数是多少人? 师:同学们,我们先来看看题目中的条件,“参加爬山和参加划船的人数之比 是5:8”,这里我们把什么作为单位“1”? 生:把全部学校的学生作为单位“1”。 师:不错,我们把单位“1”划分成5+8=13份,参加划船人数是几份?参加爬 山人数是几份? 生:…… 师:划船人数是8份,相对应的是112人,那每份多少呢?单位“1”是多少? 生:…… 师:如果我们用分数表示,则参加划船人数占总人数的几分之几? (引导学生对单位“1”复习,理清比和分率之间的相互转换) 生:…… 师:知道部分量在单位“1”中占的分率,我们用除法就可以把单位“1”的量 求出来了。 板书: 112÷=182(人) 答:秋游的总人数是182人。 练习2:(8分) 甲、乙两班人数比是4:3,其中甲班有56人,甲、乙两班一共有多少人? 分析:正确理解比的意义,运用单位“1”的知识理清总量和部分量的关系求解。 板书: 56÷=56×=98(人) 答:甲、乙两班一共有98人。
三、小结:(5分)
| |||
第二课时(50分) 一、复习导入(3分) 师:现在,大家对“比”已经有了初步了解,谁能举几个生活中“比”的例子。 (屏幕出示足球比赛场景图片,比分为3:0) 师:这是比分,这里的3:0是什么意思?你们觉得这个“比”想说明的意思和 我们今天学的“比”一样吗? 师:其实,这个3:0本身就提醒了我们它不是表示比的关系,哪里提醒我们了?(引导学生发现比的后项相当于除法中的除数,分数中的分母,不能为0) 师:这里只是用比的样子记录各自进球个数或所得分数,并不是表示两数相除 的关系,大家可要注意哦。 (出示PPT) | |||
二、探索发现授课(42分) (一)例题3:(13分) 六一班男生和女生的比是2:3,其中女生比男生多15人,求六一班有学生多少人? 师:本题中,我们把什么作为单位“1”? 生:六一班人数。 师:我们把单位“1”分成几份?那么男生占多少份?女生占多少份? (进一步让学生掌握比的基本知识,要多提问基础稍差的学生) 生:…… 师:男生和女生的比是2:3,所以男生是2份,女生是3份。从女生比男生多 15人中可以得出什么? 生:得出一份是15人。 师:不错,我们知道一份相对应的量是15人,那5份是多少? 生:15×5=75。 师:不错。如果我们用部分量和分率来表示,女生占六一班学生数的几分之几? 男生占几分之几? 生:…… 师:条件中15相对应的分率是多少? 生:…… 板书: 15÷(-) =15÷ =75(人) 答:六一班有学生75人。
练习3:(7分) 甲、乙两个工程队共修一条路,甲乙两队修的长度比是5:4,甲队比乙队多修了40米,求这条路多长? 分析:掌握比的意义和应用。甲乙两队修的长度比是5:4,把甲队修的长度当作 5份,乙队修的长度当作4份,40米相对应的就是1份,路的总长得解。
板书: 40÷(-) =40÷ =360(米) 答:这条路长360米。
(二)例题4:(13分) 一段公路长340千米,由甲、乙、丙三个工程队修,甲工程队与乙工程队完成的长度之比是2:3,甲工程队完成的是丙的,甲、乙、丙三个工程队各完成多少千米? 师:本题中出现了3个部分的量,我们不知道各个部分的量和总量的数量关系, 只知道部分的量与部分的量的关系,怎么办呢? 师:老师先来举个简单的例子,一批球中,篮球比排球的比是1:2,篮球与足球 的比是1:3,排球和足球的比是多少呢? 生:2:3。 师:不错,那同学们能告诉老师为什么吗? (引导学生对连比的初步讨论) 生:…… 师:同学们说得非常不错,在这里我们可以把篮球当作1份,那么排球就是2 份,足球就是3份了,所以排球和足球的比就是2:3了。 师:那老师再问你,篮球、排球、足球的比是多少吗? (引导学生对连比的应用转换) 生:1:2:3。 师:看来同学们都已经初步掌握了连比的应用,我们再来看看题目中的条件。 甲工程队完成的是丙的,那么甲、丙修的长度比是多少? 生:4:7。 师:甲、乙工程队完成的长度之比是2:3,那甲、乙、丙的比是2:3:7吗? (与学生进一步讨论连比的应用,以及正确转换) 生:…… 师:甲:乙=2:3,甲:丙=4:7,比中它们的份数不一样,根据比的基本性质,我 们可以转换成相同的份数,就可以求出连比了。甲:乙=2:3=4:6,甲:丙=4:7, 甲:乙:丙=4:6:7。把甲当作4份,那总数是多少份? 生:4+6+7=17(份)。 师:不错,那17份对应的量是多少? 生:340千米。 师:理清各部分量和总量的关系,我们就能快速解题了。 板书: 甲:乙=2:3=4:6 甲:丙=4:7 甲:乙:丙=4:6:7 甲:340×=80(千米) 乙:340×=120(千米) 丙:340×=140(千米) 答:甲修80千米,乙修120千米,丙修140千米。
练习4:(7分) 六年级三个班共有86人,一班与二班人数的比是5:4,二班与三班人数的比是3:4。三个班各有多少人? 分析:正确运用连比,找出部分量和总量之间的关系,快速求解。 板书: 一班:二班=5:4=15:12 二班:三班=3:4=12:16 一班:二班:三班=15:12:16 一班:86×=30(人) 二班:86×=24(人) 三班:86×=32(人) 答:一班30人,二班24人,三班32人。
(三)例题5(选讲): 甲、乙两袋糖的质量比是4:1,从甲袋中取出13千克糖放入乙袋,这时两袋糖的质量比是7:5。求甲、乙两袋糖原来各是多少? 师:我们来看下题目,从甲袋取出放入乙袋,甲袋的质量、乙袋的质量在变化, 那什么没发生变化呢? 生:两袋的总质量没有发生变化。 师:不错,看来同学们能正确的抓住不变的量来理清解题思路了。 师:原来甲占两袋糖的总质量是多少,乙呢? 生:甲占,乙占。 师:从甲袋中取出13千克糖放入乙袋后,甲占糖的质量多少呢?乙占糖的质量 多少呢? 生:甲占=,乙占。 师:在甲袋中,13千克相对应的分率是多少呢? 生:-。 师:如果按乙袋来算,13千克相对应的分率是多少呢? 生:-。 师:我们一起来算下,它们得出的答案是一样的吗? 板书: 总质量: 13÷(-)=60(千克) 或13÷(-)=60(千克) 甲袋:60×=48(千克) 乙袋:60×=12(千克) 答:甲袋48千克,乙袋12千克。
练习5(选做): 甲、乙两个仓库存大米重量比3:7,如果从乙仓库调2500千克大米到甲仓库,这时甲仓大米重量是乙仓库的,求甲、乙两仓库原来各有多少千克大米? 分析:正确理清总量和部分量的关系,找到已知量相对应的分率,求出总量, 各部分的量都可以求解了。 板书: 2500÷(-) =2500÷ =25000(千克) 甲仓库:25000×=7500(千克) 乙仓库:25000×=17500(千克) 答:甲仓库有7500千克,乙仓库有17500千克。
三、总结:(5分)
四、随堂练习: 1. 求比值。 3.5:23% : 200升:3000立方分米 板书:=3.5:0.23 =÷ =200升:3000升 = = =
2. 一个长方形的周长是49米,长和宽的比是4:3,这个长方形的面积是多少 平方米? 板书: 长:49÷2×=14(米) 宽:49÷2×=10.5(米) 14×10.5=147(平方米) 答:这个长方形的面积是147平方米。
3. 篮球比足球多20个,篮球与足球的比是7:3,求篮球与足球各是多少个? 板书: 20÷(-)=50(个) 篮球:50×=35(个) 足球:50×=15(个) 答:篮球的个数是35个,足球的个数是15个。
4. 某村粮食喜获丰收。已知收获小麦、水稻、玉米共64万吨。小麦与水稻的 比是1:3,玉米与水稻的比是2:1,这三种粮食各多少万吨? 板书: 小麦:水稻=1:3 玉米:水稻=2:1=6:3 小麦:水稻:玉米=1:3:6 小麦:64×=6.4(万吨) 水稻:64×=19.2(万吨) 玉米:64×=38.4(万吨) 答:小麦6.4万吨,水稻19.2万吨,玉米38.4万吨。
5. 甲、乙两队原有人数比为7:3,甲队抽30人到乙队,则两队人数比为3:2, 甲、乙两队原有多少人? 板书: 30÷(-)=300(人) 甲:300×=210(人) 乙:300×=90(人) 答:甲队有210人,乙队有90人。
| |||
家庭作业 | 线上作业:第6讲 | ||
主管评价 |
| ||
主管评分 |
| ||
课后反思 (不少于60字) | 整体效果 |
| |
设计不足之处 |
| ||
设计优秀之处 |
| ||
奥数六年级上册寒假课程第6讲《比例解应用题》课件+教案: 这是一份奥数六年级上册寒假课程第6讲《比例解应用题》课件+教案,文件包含奥数六年级上册寒假课程第6讲《比例解应用题》课件ppt、奥数六年级上册寒假课程第6讲《比例解应用题》教案doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
奥数六年级上册寒假课程第3讲《分数的应用》课件+教案: 这是一份奥数六年级上册寒假课程第3讲《分数的应用》课件+教案,文件包含奥数六年级上册寒假课程第3讲《分数的应用》课件ppt、奥数六年级上册寒假课程第3讲《分数的应用》教案doc等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
奥数六年级上册 第13讲:圆柱和圆锥的体积 课件+教案: 这是一份奥数六年级上册 第13讲:圆柱和圆锥的体积 课件+教案,文件包含奥数六年级上册第13讲圆柱和圆锥的体积课件pptx、奥数六年级上册第13讲圆柱和圆锥的体积教案doc等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。













