2023年山东省青岛市中考数学试卷【附答案】

这是一份2023年山东省青岛市中考数学试卷【附答案】，共14页。试卷主要包含了选择题，填空题，作图题，解答题等内容，欢迎下载使用。

2023年山东省青岛市中考数学试卷
一、选择题（本大题共10小题，每小题3分，共30分）
1．（3分）生活中有许多对称美的图形，下列是中心对称图形但不是轴对称图形的是（　　）
A． B．
C． D．
2．（3分）的相反数是（　　）
A．﹣ B． C．﹣7 D．7
3．（3分）一个正方体截去四分之一，得到如图所示的几何体，其左视图是（　　）

A． B． C． D．
4．（3分）中欧班列是共建“一带一路”的旗舰项目和明星品牌，是亚欧各国深化务实合作的重要载体．中欧班列“青岛号”自胶州开往哈萨克斯坦，全程7900公里．将7900用科学记数法表示为（　　）
A．0.79×103 B．7.9×102 C．7.9×103 D．79×102
5．（3分）如图，将线段AB先向左平移，使点B与原点O重合，则点A的对应点A′的坐标是（　　）

A．（2，﹣3） B．（﹣2，3） C．（3，﹣2） D．（﹣3，2）
6．（3分）如图，直线a∥b，∠1＝63°，则∠2的度数为（　　）

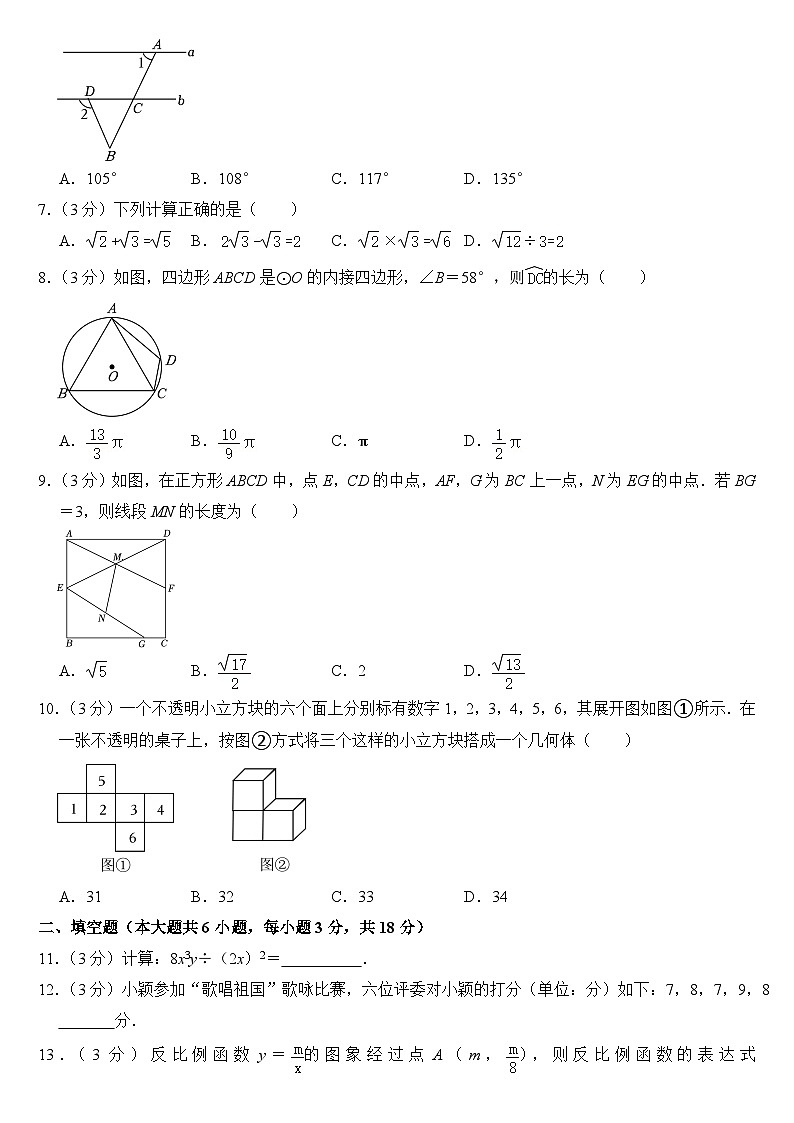
A．105° B．108° C．117° D．135°
7．（3分）下列计算正确的是（　　）
A． B． C． D．
8．（3分）如图，四边形ABCD是⊙O的内接四边形，∠B＝58°，则的长为（　　）

A． B． C．π D．
9．（3分）如图，在正方形ABCD中，点E，CD的中点，AF，G为BC上一点，N为EG的中点．若BG＝3，则线段MN的长度为（　　）

A． B． C．2 D．
10．（3分）一个不透明小立方块的六个面上分别标有数字1，2，3，4，5，6，其展开图如图①所示．在一张不透明的桌子上，按图②方式将三个这样的小立方块搭成一个几何体（　　）

A．31 B．32 C．33 D．34
二、填空题（本大题共6小题，每小题3分，共18分）
11．（3分）计算：8x3y÷（2x）2＝　 　．
12．（3分）小颖参加“歌唱祖国”歌咏比赛，六位评委对小颖的打分（单位：分）如下：7，8，7，9，8　 　分．
13．（3分）反比例函数y＝的图象经过点A（m，），则反比例函数的表达式为 　 　．
14．（3分）某校组织学生进行劳动实践活动，用1000元购进甲种劳动工具，用2400元购进乙种劳动工具，但单价贵了4元．设甲种劳动工具单价为x元，则x满足的分式方程为 　 　．
15．（3分）如图，在平面直角坐标系中，已知点A（1，0），P（﹣1，0），且与x轴交于另一点D，AB为⊙P的切线，BC是⊙P的直径，则∠BCD的度数为 　 　°．

16．（3分）如图，二次函数y＝ax2+bx+c的图象与正比例函数y＝kx的图象相交于A，B两点，已知点A的横坐标为﹣3，二次函数图象的对称轴是直线x＝﹣1．下列结论：①abc＜0；②3b+2c＞02+bx+c＝kx的两根为x1＝﹣3，x2＝2；④k＝a．其中正确的是 　 　.（只填写序号）

三、作图题（本大题满分4分）
17．（4分）请用直尺、圆规作图，不写作法，但要保留作图痕迹．
已知：△ABC．
求作：点P，使PA＝PC，且点P在△ABC边AB的高上．

四、解答题（本大题共9小题，共68分）
18．（8分）（1）解不等式组：；
（2）计算：（m﹣）•．
19．（6分）今年4月15日是我国第八个“全民国家安全教育日”．为增强学生国家安全意识，夯实国家安全教育基础、某市举行国家安全知识竞赛．竞赛结束后，发现所有参赛学生的成绩（满分100分）（用x表示）分为四组：A组（60≤x＜70），B组（70≤x＜80）（80≤x＜90），D组（90≤x≤100），绘制了如图不完整的频数分布直方图和扇形统计图．

根据以上信息，解答下列问题：
（1）补全频数分布直方图；
（2）扇形统计图中A组所对应的圆心角的度数为 　 　°；
（3）把每组中各个同学的成绩用这组数据的中间值（如A组：60≤x＜70的中间值为65）来代替，试估计小明班级的平均成绩；
（4）小明根据本班成绩，估计全市参加竞赛的所有8000名学生中会有800名学生成绩低于70分，实际只有446名学生的成绩低于70分．请你分析小明估计不准确的原因．
20．（6分）为了解我国的数学文化，小明和小红从《九章算术》《孙子算经》《海岛算经》（依次用A、B、C表示）三本书中随机抽取一本进行阅读，小红再从剩下的两本中随机抽取一本．请用列表或画树状图的方法表示所有可能出现的结果．并求抽取两本书中有《九章算术》的概率．
21．（6分）太阳能路灯的使用，既方便了人们夜间出行，又有利于节能减排．某校组织学生进行综合实践活动——测量太阳能路灯电池板的宽度．如图，点O是AB的中点，OC是灯杆．地面上三点D，DE＝1.5m，EC＝5m．该校学生在D处测得电池板边缘点B的仰角为37°（结果精确到0.1m．参考数据：sin37°≈，cos37°≈，tan37°≈，≈1.41）

22．（6分）如图①，正方形ABCD的面积为1．
（1）如图②，延长AB到A1，使A1B＝BA，延长BC到B1，使B1C＝CB，则四边形AA1B1D的面积为 　 　；
（2）如图③，延长AB到A2，使A2B＝2BA，延长BC到B2，使B2C＝2CB，则四边形AA2B2D的面积为 　 　；
（3）延长AB到An，使AnB＝nBA，延长BC到Bn，使BnC＝nCB，则四边形AAnBnD的面积为 　 　．
23．（8分）某服装店经销A，B两种T恤衫，进价和售价如下表所示：
品名
A
B
进价（元/件）
45
60
售价（元/件）
66
90
（1）第一次进货时，服装店用6000元购进A，B两种T恤衫共120件
（2）受市场因素影响，第二次进货时，A种T恤衫进价每件上涨了5元，但两种T恤衫的售价不变．服装店计划购进A，B两种T恤衫共150件，两种T恤衫全部售完可获利W元．
①请求出W与m的函数关系式；
②服装店第二次获利能否超过第一次获利？请说明理由．
24．（8分）如图，在▱ABCD中，∠BAD的平分线交BC于点E，点G，H分别是AE和CF的中点．
（1）求证：△ABE≌△CDF；
（2）连接EF．若EF＝AF，请判断四边形GEHF的形状，并证明你的结论．

25．（10分）许多数学问题源于生活．雨伞是生活中的常用物品，我们用数学的眼光观察撑开后的雨伞（如图①）、可以发现数学研究的对象——抛物线．在如图②所示的直角坐标系中，坐标原点O为伞骨OA，OB的交点．点C为抛物线的顶点，B在抛物线上，OA、OB关于y轴对称．OC＝1分米，A，B两点之间的距离是4分米．
（1）求抛物线的表达式；
（2）分别延长AO，BO交抛物线于点F，E，求E；
（3）以抛物线与坐标轴的三个交点为顶点的三角形面积为S1，将抛物线向右平移m（m＞0）个单位，得到一条新抛物线2．若S2＝S1，求m的值．

26．（10分）如图，在菱形ABCD中，对角线AC，AB＝10cm，BD＝4，沿AB方向匀速运动，速度为1cm/s，动点Q从点A出发，沿AD方向匀速运动，AQ为邻边的平行四边形APMQ的边PM与AC交于点E．设运动时间为t（s）（0＜t≤5），解答下列问题：
（1）当点M在BD上时，求t的值；
（2）连接BE．设△PEB的面积为S（cm2），求S与t的函数关系式和S的最大值；
（3）是否存在某一时刻t，使点B在∠PEC的平分线上？若存在，求出t的值，请说明理由．


1．D．
2．A．
3．D．
4．C．
5．A．
6．B．
7．C．
8．C．
9．B．
10．B．
11．解：原式＝8x3y÷8x2
＝2xy，
12．解：∵这组数据的最大值是10，最小值是7，
∴这六个分数的极差是：10﹣7＝8（分），
13．解：∵反比例函数y＝的图象经过点A（m，），
∴＝m．
∴m＝8，
∴反比例函数解析式为：y＝．
14．解：∵乙种劳动工具的单价比甲种劳动工具的单价贵了4元，且甲种劳动工具单价为x元，
∴乙种劳动工具单价为（x+4）元．
根据题意得：＝2×．
15．解：∵点A（1，0），5），
∴OP＝OA＝1，
∴AP＝OP+OA＝2
∵⊙P过原点O，
∴OP为⊙P的半径，
∵AB为⊙P的切线，
∴PB⊥AB，PB＝OP＝8，
在Rt△ABP中，BP＝1，sinA＝PB/AP＝1/6，
∴∠BAP＝30°，
∴∠BPA＝60°，
∴∠CPD＝60°，
又∵PC＝PD，
∴三角形CPD为等边三角形，
∴∠PCD＝60°，
即∠BCD的度数为60°．
16．解：由图象可得，a＞0，又﹣，
∴b＞8．
∴abc＜0．
∴①正确．
由题意，令ax2+bx+c＝kx，
∴ax5+（b﹣k）x+c＝0．
又二次函数y＝ax2+bx+c的图象与正比例函数y＝kx的图象相交于A，B两点，点B的横坐标为5，
∴ax2+（b﹣k）x+c＝0的两根之和为﹣5+2＝﹣1，两根之积为﹣2×2＝﹣6．
∴﹣＝﹣6，．
∴6a+c＝0．
又b＝4a，
∴3b+c＝0．
∴5b+2c＝c＜0．
∴②错误，③正确．
∵﹣＝﹣6，
∴k＝a．
∴④错误．
故答案为：①③．
17．
18．（1）解第一个不等式得：x＜3，
解第二个不等式得：x≥1，
故原不等式组的解集为：4≤x＜3；
（2）原式＝•
＝•
＝m+2．
19．解：（1）由频数分布直方图可知：C组是10人，
由扇形统计图可知：C组占班级人数的20%，
∴班级人数为：10÷25%＝40（人），
∴B组的人数为：40﹣4﹣10﹣18＝8（人），
∴补全频数分布直方图如图所示：

（2）由频数分布直方图可知：C组是4人，
∴A组人数占班级人数的百分比为：4÷40＝10%，
∴A组所对应的圆心角的度数为：360°×40%＝36°．
故答案为：36．
（3）∵A组中间值为65分，A组有4人，B组有2人，C组有10人，D组有18人，
∴班级的平均成绩为：（65×4+75×8+85×10+95×18）＝85.2（分），
答：估计小明班级的平均成绩为85.5分．
（4）∵小明班级低于70分的人数占班级人数的10%，
∴8000×10%＝800（人），
因此小明估计全市低于70分的人数有800人．
其实这样估计是不准确，其原因是：小明班级的这个样本只能代表小明学校，不能用来估计全市所有学校学生的成绩，只要合理即可）．
20．解：画树状图为：

共有6种等可能的结果，其中抽取两本书中有《九章算术》的结果数为4种，
所以抽取两本书中有《九章算术》的概率＝＝．
21．解：过点B作BH⊥DC于点H，过点B作BF⊥OC于点F，
 
依题意得：OC⊥DC，∠BDH＝37°，
又BH⊥DC
∴△BEH和△OEC均为等腰直角三角形，
∴EH＝BH，EC＝OC，
∵DE＝1.5m，EC＝6m，
∴OC＝EC＝5m，
∵BH⊥DC，BF⊥OC，
∴四边形BHCF为矩形，
∴BF＝CH，BH＝CF，
∴∠OBF＝∠NEH＝45°，
∴△OBF为等腰直角三角形，
∴BF＝OF＝CH，
设BF＝xm，则OF＝CH＝xm，
∴EH＝BH＝EC﹣CH＝（5﹣x） m，
∴DH＝DE+EH＝3.5+5﹣x＝（4.5﹣x） m，
在Rt△BDH中，tan∠BDH＝，
即：tan37°＝，
∴，
解得：x＝0.5，
检验后知道x＝7.5是原方程得根．
∴BF＝OF＝0.6（m），
在等腰Rt△OBF中，由勾股定理得：OB＝≈0.5×6.41＝0.705（m），
∵点O为AB的中点，
∴AB＝2OB≈4×0.705≈1.4（m），
答：太阳能电池板宽AB的长度约为1.4m．
22．解：（1）∵正方形ABCD的面积为1，
∴AB＝BC＝CD＝AD＝1，
∵A2B＝BA，B1C＝CB，
∴BB1＝BC+CB3＝2，A1B＝2，
∵A1B⊥BB1，
∴S△ABB8＝A2B×BB1＝×1×2＝7，
∵AD⊥AB，
∴S梯形ABB1D＝（BB1+AD）×AB＝（2+1）×8＝，
∵S四边形AA3B1D＝S△ABB1+S梯形ABB5D，
∴S四边形AA1B1D＝3+＝2.5，
故答案为：2.4；
（2））∵正方形ABCD的面积为1，
∴AB＝BC＝CD＝AD＝1，
∵A3B＝2BA＝2，B2C＝2CB＝2，
∴BB6＝BC+CB2＝2+2＝3，A2B＝6，
∵A2B⊥BB2，
∴＝A6B×BB2＝×2×（2+8）＝，
∵AD⊥AB，
∴＝（BB4+AD）×AB＝（5+1+1）×3＝2，
∵＝+，
∴＝3+3＝5，
故答案为：5；
（3）∵正方形ABCD的面积为3，
∴AB＝BC＝CD＝AD＝1，
∵AnB＝nBA＝n，BnC＝nCB＝n，
∴BBn＝BC+CBn＝n+1，AnB＝n，
∵AnB⊥BBn，
∴＝AnB×BBn＝×n×（n+1）＝，
∵AD⊥AB，
∴＝（BBn+AD）×AB＝（n+1+6）×1＝，
∵＝+，
∴＝n（n+4）+（n2+7n+2），
故答案为：（n2+2n+4）．
23．解：（1）设购进AT恤衫x件，购进BT恤衫y件
，
解得，
∴全部售完获利＝（66﹣45）×80+（90﹣60）×40＝1680+1200＝2880（元）．
（2）①设第二次购进A种T恤衫m件，则购进B种T恤衫（150﹣m）件，即m≥50，
∴W＝（66﹣45﹣5）m+（90﹣60﹣10）（150﹣m）＝﹣4m+3000（150≥m≥50），
②服装店第二次获利不能超过第一次获利，理由如下：
由①可知，W＝﹣3m+3000（150≥m≥50），
∵﹣4＜0，一次函数W随m的增大而减小，
∴当m＝50时，W取最大值，W大＝﹣7×50+3000＝2800（元），
∵2800＜2880，
∴服装店第二次获利不能超过第一次获利．
24．（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AB＝CD，∠B＝∠D，∠DFC＝∠BCF，
∵∠BAD和∠DCB的平分线AE、CF分别交BC、F，
∴∠BAE＝∠DAE＝∠BAD∠DCB，
∴∠BAE＝∠DCF，
在△BAE和△DCF中，
，
∴△BAE≌△DCF（ASA）．
（2）证明：∵△BAE≌△DCF，
∴AE＝CF，∠AEB＝∠DFC，
∴∠AEB＝∠BCF，
∴AE∥CF，
∵点G、H分别为AE，
∴GE∥FH，GE＝FH，
∴四边形FGEH是平行四边形
∵EF＝AF，G为AE的中点，
∴GF⊥AE，
∴四边形FGEH是矩形．
25．解：（1）设抛物线的表达式为：y＝ax2+c，
由题意得，点A的坐标为：（2、点C（3，
则，解得：，
则抛物线的表达式为：y＝﹣0.6x2+1①；

（2）由点A的坐标得，直线OA的表达式为：y＝5.3x②，
联立①②得：0.8x＝﹣0.1x7+1，
解得：x＝2（舍去）或﹣8，
即点F（﹣5，﹣1.7），
则EF＝5×2＝10；
（3）平移后的抛物线表达式为：y＝﹣8.1（x﹣m）2+6，
令x＝0，则y＝﹣0.8m2+1，此时抛物线与y轴的交点为D（42+1），
∵平移前后抛物线和x轴交点间的距离不变，若S2＝S5，
则OD＝OC，
即﹣6.1m2+8＝×8，
解得：m＝±2（舍去负值），
即m＝2．
26．解：（1）由题意得：DQ＝10﹣2t，PM＝2t，QM＝AP＝t，
如下图，点M在BD上时，

∵QM∥PB，PM∥QD，
∴∠DQM＝∠DAB＝∠MPQ，∠DMQ＝∠MBP，
∴△DQM∽△MPB，则，
即，
解得：t＝；
（2）如上图，
∵AD∥PM，
∴∠AEP＝∠EAQ，
∵四边形ABCD是菱形，
则∠QAE＝∠EAP，
∴∠AEP＝∠EAP，
∴△APE为等腰三角形，则PE＝AP＝t，
过点D作DH⊥AB于点H，
则S△ABD＝AB•DH＝，
即10•DH＝×4，
解得：DH＝5，则sin∠DAH＝＝＝，
设△PEB中PB边上的高为h，
则S＝PB•h＝（20﹣t）×t2+3t（0＜t≤5），
∵﹣＜0，当t＝4时，S的最大值为10；
（3）存在，理由：
如下图，过点B作BR⊥PE于点R，
当点B在∠PEC的平分线上时，则BR＝OB＝2，
在Rt△PBR中，sin∠EPB＝sin∠DAB＝＝＝，
解得：t＝．