2012年江西省中考数学试卷

这是一份2012年江西省中考数学试卷，共8页。试卷主要包含了﹣1的绝对值是，下列运算正确的是等内容，欢迎下载使用。

2012年江西省中考数学试卷　
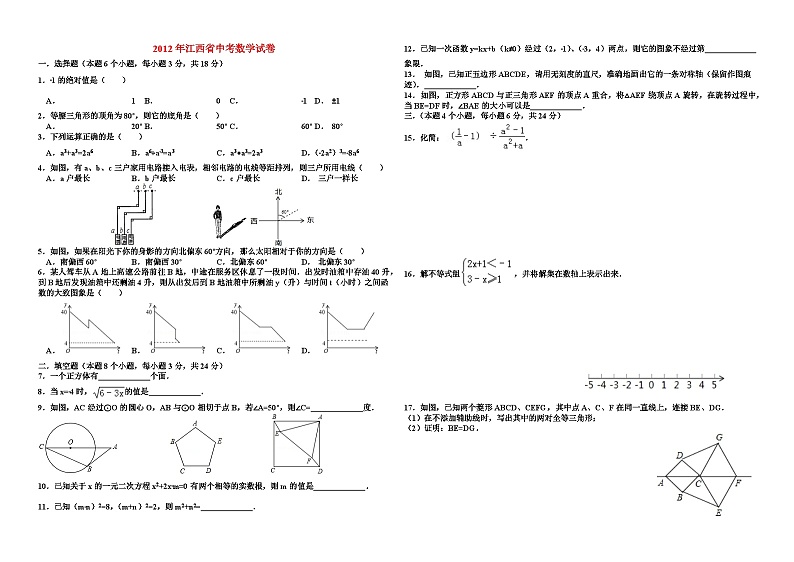
一．选择题（本题6个小题，每小题3分，共18分）
1．﹣1的绝对值是（　　）
　 A． 1 B． 0 C． ﹣1 D． ±1
2．等腰三角形的顶角为80°，则它的底角是（　　）
　 A． 20° B． 50° C． 60° D． 80°
3．下列运算正确的是（　　）
　 A．a3+a3=2a6 B．a6÷a﹣3=a3 C．a3•a3=2a3 D．（﹣2a2）3=﹣8a6
4．如图，有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线（　　）
　 A．a户最长 B．b户最长 C．c户最长 D． 三户一样长

5．如图，如果在阳光下你的身影的方向北偏东60°方向，那么太阳相对于你的方向是（　　）
　 A．南偏西60° B．南偏西30° C．北偏东60° D． 北偏东30°
6．某人驾车从A地上高速公路前往B地，中途在服务区休息了一段时间．出发时油箱中存油40升，到B地后发现油箱中还剩油4升，则从出发后到B地油箱中所剩油y（升）与时间t（小时）之间函数的大致图象是（　　）
　 A． B． C． D．
二．填空题（本题8个小题，每小题3分，共24分）
7．一个正方体有　_________　个面．
8．当x=﹣4时，的值是　_________　．
9．如图，AC经过⊙O的圆心O，AB与⊙O相切于点B，若∠A=50°，则∠C=　_________　度．

10．已知关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值是　_________　．
11．已知（m﹣n）2=8，（m+n）2=2，则m2+n2=　_________　．
12．已知一次函数y=kx+b（k≠0）经过（2，﹣1）、（﹣3，4）两点，则它的图象不经过第　_________　象限．
13． 如图，已知正五边形ABCDE，请用无刻度的直尺，准确地画出它的一条对称轴（保留作图痕迹）．　_________　．
14．如图，正方形ABCD与正三角形AEF的顶点A重合，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，∠BAE的大小可以是　_________　．
三．（本题4个小题，每小题6分，共24分）
15．化简：．










16．解不等式组，并将解集在数轴上表示出来．










17．如图，已知两个菱形ABCD、CEFG，其中点A、C、F在同一直线上，连接BE、DG．
（1）在不添加辅助线时，写出其中的两对全等三角形；
（2）证明：BE=DG．





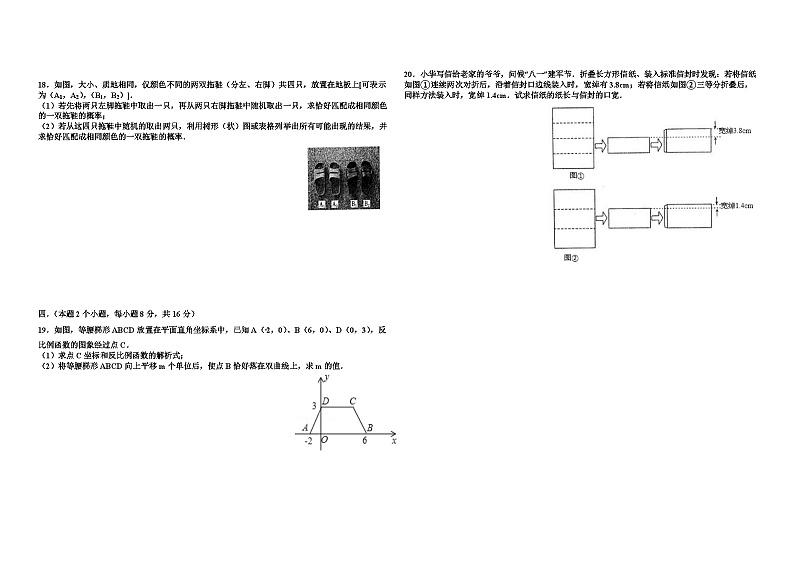
18．如图，大小、质地相同，仅颜色不同的两双拖鞋（分左、右脚）共四只，放置在地板上[可表示为（A1，A2），（B1，B2）]．
（1）若先将两只左脚拖鞋中取出一只，再从两只右脚拖鞋中随机取出一只，求恰好匹配成相同颜色的一双拖鞋的概率；
（2）若从这四只拖鞋中随机的取出两只，利用树形（状）图或表格列举出所有可能出现的结果，并求恰好匹配成相同颜色的一双拖鞋的概率．










四．（本题2个小题，每小题8分，共16分）
19．如图，等腰梯形ABCD放置在平面直角坐标系中，已知A（﹣2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．
（1）求点C坐标和反比例函数的解析式；
（2）将等腰梯形ABCD向上平移m个单位后，使点B恰好落在双曲线上，求m的值．










20．小华写信给老家的爷爷，问候“八一”建军节．折叠长方形信纸、装入标准信封时发现：若将信纸如图①连续两次对折后，沿着信封口边线装入时，宽绰有3.8cm；若将信纸如图②三等分折叠后，同样方法装入时，宽绰1.4cm．试求信纸的纸长与信封的口宽．




























五．（本题2个小题，每小题9分，共18分）
21．我们约定：如果身高在选定标准的±2%范围之内都称为“普通身高”．为了解某校九年级男生中具有“普通身高”的人数，我们从该校九年级男生中随机选出10名男生，分别测量出他们的身高（单位：cm）收集并整理如下统计表：
男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
身高
163
171
173
159
161
174
164
166
169
164
（1）计算这组数据的三个统计量：平均数、中位数和众数；
（2）请你选择一个统计量作为选定标准，找出这10名具有“普通身高”的是哪几位男生？并说明理由；
（3）若该年级共有280名男生，按（2）中选定标准，请你估算出该年级男生中“普通身高”的人数约有多少名？




































22．如图1，小红家阳台上放置了一个晒衣架．如图2是晒衣架的侧面示意图，立杆AB、CD相交于点O，B、D两点立于地面，经测量：
AB=CD=136cm，OA=OC=51cm，OE=OF=34cm，现将晒衣架完全稳固张开，扣链EF成一条直线，且EF=32cm．
（1）求证：AC∥BD；
（2）求扣链EF与立杆AB的夹角∠OEF的度数（精确到0.1°）；
（3）小红的连衣裙穿在衣架后的总长度达到122cm，垂挂在晒衣架上是否会拖落到地面？请通过计算说明理由．
（参考数据：sin61.9°≈0.882，cos61.9°≈0.471，
tan61.9°≈0.553；可使用科学记算器）



























六．（本题2个小题，每小题10分，共20分）
23．如图，已知二次函数L1：y=x2﹣4x+3与x轴交于A、B两点（点A在点B的左边），与y轴交于点C．
（1）写出A、B两点的坐标；
（2）二次函数L2：y=kx2﹣4kx+3k（k≠0），顶点为P．
①直接写出二次函数L2与二次函数L1有关图象的两条相同的性质；
②是否存在实数k，使△ABP为等边三角形？如果存在，请求出k的值；如不存在，请说明理由；
③若直线y=8k与抛物线L2交于E、F两点，问线段EF的长度是否会发生变化？如果不会，请求出EF的长度；如果会，请说明理由．






























24．已知，纸片⊙O的半径为2，如图1，沿弦AB折叠操作．
（1）如图2，当折叠后的经过圆心O时，求的长；
（2）如图3，当弦AB=2时，求折叠后所在圆的圆心O′到弦AB的距离；
（3）在图1中，再将纸片⊙O沿弦CD折叠操作．
①如图4，当AB∥CD，折叠后的与所在圆外切于点P时，设点O到弦AB、CD的距离之和为d，求d的值；
②如图5，当AB与CD不平行，折叠后的与所在圆外切于点P时，设点M为AB的中点，点N为CD的中点．试探究四边形OMPN的形状，并证明你的结论．



2012年江西省中考数学试卷参考答案
1．A2．B3．D4．D5．A6．C
7．　6　．8．　3　．9．　20　．10．　﹣1　．11．　5　．12．　三　．
13．解：如图所示，直线AK即为所求的一条对称轴（解答不唯一）．

14．　15°或165°　．
15．解：（﹣1）÷
=÷ …（3分）
=• …（4分）
=•
=﹣1．…（6分）
16．解：
解不等式（1）得：x＜﹣1
解不等式（2）得：x≤2，
所以不等式组的解集是：x＜﹣1．
在数轴上表示出不等式的解集，如图所示：

17．（1）解：△ADC≌△ABC，△GFC≌△EFC；
（2）证明：∵四边形ABCD、CEFG是菱形，
∴DC=BC，CG=CE，∠DCA=∠BCA，∠GCF=∠ECF，
∵∠ACF=180°，
∴∠DCG=∠BCE，
在△DCG和△BCE中
∵，
∴△DCG≌△BCE，
∴BE=DG．
18．解：（1）∵若先将两只左脚拖鞋中取出一只，再从两只右脚拖鞋中随机取出一只，有A1A2，A1B2，B1B2，B1A2四种情况，恰好匹配的有A1A2，B1B2两种情况；
∴P（恰好匹配）=…2分
（2）方法一：画树形图如下：

∵所有可能的结果为A1A2，A1B1，A1B2；A2A1，A2B1，A2B2；B1A1，B1A2，B1B2；B2A1，B2A2，B2B1…4分
∴从这四只拖鞋中随机的取出两只，共有12种不同的情况，其中恰好匹配的有4种，分别是A1A2，A2A1，B1B2，B2B1．
∴P（恰好匹配）=．…6分
方法二：列表格如下：
A1B2 A2B2 B1B2 ﹣
A1B1 A2B1 ﹣ B2B1
A1A2 ﹣ B1A2 B2A2
﹣ A2A1 B1A1 B2A1
其中恰好匹配的有4种，分别是A1A2，A2A1，B1B2，B2B1．
∴P（恰好匹配）=．…6分
19．解：（1）过点C作CE⊥AB于点E，
∵四边形ABCD是等腰梯形，
∴AD=BC，DO=CE，
∵∠DOA=∠CEO=90°，
在Rt△AOD和Rt△BEC中
∵，
∴Rt△AOD≌Rt△BEC，
∴AO=BE=2，
∵BO=6，
∴DC=OE=4，
∴C（4，3），
∵设反比例函数的解析式y=，
根据题意得：3=，
解得k=12，
∴反比例函数的解析式；
答：点C坐标是（4，3），反比例函数的解析式是y=．
（2）将等腰梯形ABCD向上平移m个单位后得到梯形A′B′C′D′，
∴点B′（6，m），
∵点B′（6，m）恰好落在双曲线y=上，
∴当x=6时，m==2，
即m=2．

20．解：解法一：
设信纸的纸长为xcm，
根据题意得：+3.8=+1.4，
解得x=28.8；
所以信封的口宽为+3.8=11（cm），
答：信纸的纸长为28.8cm，信封的口宽为11cm．
解法二：
设信封的口宽为ycm，
根据题意得：4（y﹣3.8）=3（y﹣1.4），
解得y=11；
所以信纸的纸长为4×（11﹣3.8）=28.8（cm）．
答：信纸的纸长为28.8cm，信封的口宽为11cm．
解法三：设信纸的长度为xcm、信封的口宽为ycm，
根据题意得：
解得：
答：信纸的纸长为28.8cm，信封的口宽为11cm．
21．解：（1）平均数为：
=166.4（cm），
中位数为：=165（cm），
众数为：164cm；
（2）选平均数作为标准：
身高x满足166.4×（1﹣2%）≤x≤166.4×（1+2%），
即163.072≤x≤169.728时为“普通身高”，
此时⑦、⑧、⑨、⑩男生的身高具有“普通身高”，
选中位数作为标准：
身高x满足165×（1﹣2%）≤x≤165×（1+2%），
即161.7≤x≤168.3时为“普通身高”，
此时①、⑦、⑧、⑩男生的身高具有“普通身高”；
选众数作为标准：
身高x满足164×（1﹣2%）≤x≤164×（1+2%），
即160.72≤x≤167.28时为“普通身高”，
此时①、⑤、⑦、⑧、⑩男生的身高具有“普通身高”，
（3）以平均数作为标准，估计全年级男生中“普通身高”的人数约为：
（人），
以中位数作为标准，估计全年级男生中“普通身高”的人数约为：
（人），
以众数数作为标准，估计全年级男生中“普通身高”的人数约为：
（人）．
22．（1）证明：证法一：∵AB、CD相交于点O，
∴∠AOC=∠BOD…1分
∵OA=OC，
∴∠OAC=∠OCA=（180°﹣∠BOD），
同理可证：∠OBD=∠ODB=（180°﹣∠BOD），
∴∠OAC=∠OBD，…2分
∴AC∥BD，…3分
证法二：AB=CD=136cm，OA=OC=51cm，
∴OB=OD=85cm，
∴…1分
又∵∠AOC=∠BOD
∴△AOC∽△BOD，
∴∠OAC=∠OBD；…2分
∴AC∥BD…3分；
（2）解：在△OEF中，OE=OF=34cm，EF=32cm；
作OM⊥EF于点M，则EM=16cm；…4分
∴cos∠OEF=0.471，…5分
用科学记算器求得∠OEF=61.9°…6分；
（3）解法一：小红的连衣裙会拖落到地面；…7分
在Rt△OEM中，=30cm…8分，
过点A作AH⊥BD于点H，
同（1）可证：EF∥BD，
∴∠ABH=∠OEM，则Rt△OEM∽Rt△ABH，
∴…9分
所以：小红的连衣裙垂挂在衣架后的总长度122cm＞晒衣架的高度AH=120cm．
解法二：小红的连衣裙会拖落到地面；…7分
同（1）可证：EF∥BD，∴∠ABD=∠OEF=61.9°；…8分
过点A作AH⊥BD于点H，在Rt△ABH中
，
AH=AB×sin∠ABD=136×sin61.9°=136×0.882≈120.0cm…9分
所以：小红的连衣裙垂挂在衣架后的总长度122cm＞晒衣架的高度AH=120cm．

23．解：（1）当y=0时，x2﹣4x+3=0，
∴x1=1，x2=3；
即：A（1，0），B（3，0）；

（2）①二次函数L2与L1有关图象的两条相同的性质：
（Ⅰ）对称轴都为直线x=2或顶点的横坐标为2；
（Ⅱ）都经过A（1，0），B（3，0）两点；
②存在实数k，使△ABP为等边三角形．
∵y=kx2﹣4kx+3k=k（x﹣2）2﹣k，
∴顶点P（2，﹣k）．
∵A（1，0），B（3，0），∴AB=2
要使△ABP为等边三角形，必满足|﹣k|=，
∴k=±；
③线段EF的长度不会发生变化．
∵直线y=8k与抛物线L2交于E、F两点，
∴kx2﹣4kx+3k=8k，
∵k≠0，∴x2﹣4x+3=8，
∴x1=1，x2=5，
∴EF=x2﹣x1=6，
∴线段EF的长度不会发生变化．

24．解：（1）如图2，过点O作OE⊥AB交⊙O于点E，连接OA、OB、AE、BE
∵点E与点O关于AB对称
∴△OAE、△OBE为等边三角形；…1分
∴∠OEA=∠OEB=60°
∴==；…2分
（2）如图3，连接O′A、O′B，
∵折叠前后所在的⊙O与⊙O′是等圆，
∴O′A=O′B=OA=AB=2
∴△AO′B为等边三角形；…3分
过点O′作O′E⊥AB于点E
∴O′E=O′B•sin60°=；…4分
（3）①如图4，与所在圆外切于点P时，
过点O作EF⊥AB交于点E，交于点F，
∵AB∥CD，
∴EF垂直平分CD、且必过点P，…5分
根据垂径定理及折叠，可知，…6分
又∵EF=4，
∴点O到AB、CD的距离之和为：
d=PH+PG=；…7分
②如图5，当AB与CD不平行时，
四边形OMPN是平行四边形…8分
证明如下：
设O′、O″为和所在圆的圆心，
∵O′与O关于AB对称，O″与O关于CD对称，
∴M为OO′的中点，N为OO′的中点；…9分
∵所在圆外切，
∴连心线O′O″必过点P，
∵所在圆与⊙O都是等圆，
∴O′P=O″P=2；
∴；
∴四边形OMPN是平行四边形．