专项3 一元一次方程—2023年人教版七年级上册数学期末考试复习方案（解析版）

这是一份专项3 一元一次方程—2023年人教版七年级上册数学期末考试复习方案（解析版），共8页。
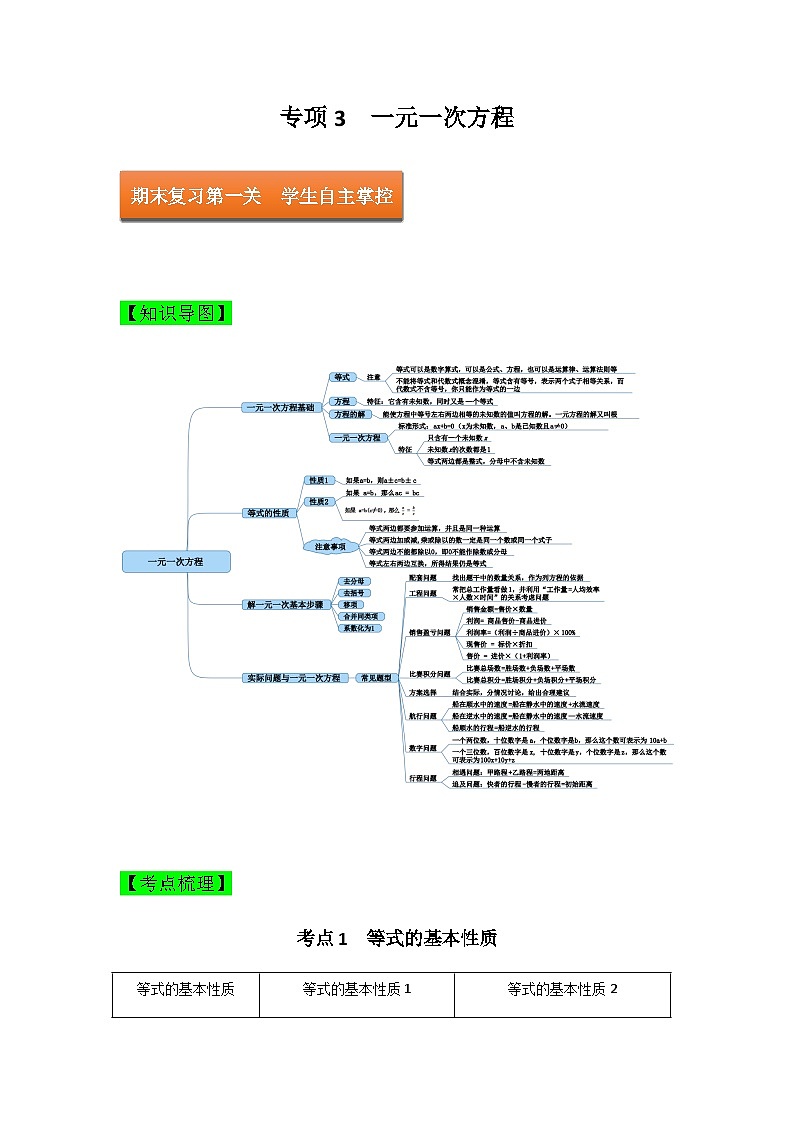
专项3  一元一次方程  【知识导图】 【考点梳理】考点1  等式的基本性质等式的基本性质等式的基本性质1等式的基本性质2简易表述同加减，仍相等同乘除，也相等，条件为数或式子为数或式子，作除时考点2  解一元一次方程1．解一元一次方程的基本步骤变形名称具体做法注意事项去分母在方程两边都乘以各分母的最小公倍数（1）不要漏乘不含分母的项（2）分子是一个整体的，去分母后应加上括号去括号先去小括号，再去中括号，最后去大括号（1）不要漏乘括号里的项（2）不要弄错符号移项把含有未知数的项都移到方程的一边，其他项都移到方程的另一边(记住移项要变号)（1）移项要变号（2）不要丢项合并同类项把方程化成的形式字母及其指数不变系数化成1在方程两边都除以未知数的系数a，得到方程的解．不要把分子、分母写颠倒2．一元一次方程的解的情况方程的解的情况方程的条件有唯一的解有无数个解无解考点3  一元一次方程的解的运用类型策略知解求参型把方程的解代入方程，求出参数整数解型先解含参方程，再利用整除的性质求解解的关系型先解含参方程，利用解的关系建立参数的方程，解方程求出参数错解型错解代入错方程，正解代入正方程新定义型按新定义列出方程再解方程遮挡型把遮挡部分作为参数，转化为知解求参型程序图型把输入作为未知数，按程序设计建立方程，解方程，如果程序是循环的，需要多次建立方程求解考点4  列方程解应用题1．常用分析法（1）直译法：找出关键词→把关键词翻译为数学符号→写出等量关系；（2）模型法：找出试题所属类型→根据类型的量得出等量关系→写出等量关系；2．常见模型行程问题，工程问题，营销问题，调配问题，配套问题，数字问题，和差积商问题，古代问题【基础百练】1．下列等式变形正确的是（　　）A．如果ax＝ay，那么x＝y B．如果a＝b，那么a﹣5＝5﹣bC．如果a＝b，那么2a＝3b D．如果a+1＝b+1，那么a＝b【答案】D【分析】根据等式基本性质逐项分析即可．【详解】A. 如果ax＝ay，且，那么x＝y，故该选项不正确，不符合题意；    B. 如果a＝b，那么a﹣5＝b﹣5，故该选项不正确，不符合题意；C. 如果a＝b，那么2a＝2b，故该选项不正确，不符合题意；    D. 如果a+1＝b+1，那么a＝b，故该选项正确，符合题意；故选D【点睛】本题考查了等式的性质，熟练等式的性质是解题的关键．等式的性质1：等式两边加(或减)同一个数(或式子)，结果仍相等；等式的性质2：等式两边乘同一个数，或除以同一个不为0的数(或式子)，结果仍相等．2．方程去分母后，所得结果正确的是（   ）A．  B．C．  D．【答案】B【详解】解：，去分母，方程两边同时乘以6，，，故选：B．【点睛】本题考查解一元一次方程，解题关键是解方程去分母时，方程的每一项都要乘分母的最小公倍数；括号前是负号，去括号时，括号里的各项都要变号．3．若是方程解，则的值为（  ）A． B． C． D．【答案】C【分析】把代入，解出，即可．【详解】∵是方程解，∴，∴，解得：．故选：C．【点睛】本题考查了一元一次方程的知识，解题的关键是掌握一元一次方程的解．4.为了丰富学生课后服务活动，某校七年级开展了篮球兴趣班和足球兴趣班，现需要给每名兴趣班同学分别购买一个篮球或一个足球，篮球每个100元，足球每个80元，结合图中两个学生的一段对话，求两个兴趣班各有多少人？【答案】参加篮球兴趣班的学生有120人，参加足球兴趣班的学生有150人【分析】设参加篮球兴趣班的学生有x人，则参加足球兴趣班的学生有人，根据买篮球和足球的总费用相等列方程，然后解方程即可．【详解】解：设参加篮球兴趣班的学生有x人，则参加足球兴趣班的学生有人根据题意，得：，解得，（人）．答：参加篮球兴趣班的学生有120人，参加足球兴趣班的学生有150人．【点睛】此题考查了列一元一次方程解应用题，找准等量关系准确列出方程是解题的关键．  16．计算：．圆圆在做作业时，发现题中有一个数字被墨水污染了．(1)如果被污染的数字是，请计算．(2)如果计算结果等于6，求被污染的数字．【答案】(1)-9(2)3 【分析】（1）根据有理数混合运算法则计算即可；（2）设被污染的数字为x，由题意，得，解方程即可；【详解】（1）解：；（2）设被污染的数字为x，由题意，得，解得，所以被污染的数字是3．【点睛】本题主要考查有理数的混合运算、一元一次方程的应用，掌握相关运算法则和步骤是接替的关键．17．某超市第一次以4450元购进甲、乙两种商品，其中乙商品的件数是甲商品件数的2倍多15件，甲、乙两种商品的进价和售价如下表：（注：利润＝售价－进价） 甲乙进价（元/件）2030售价（元/件）2540(1)该超市第一次购进甲、乙两种商品各多少件？(2)该超市第二次以第一次的进价又购进甲、乙两种商品，其中乙商品的件数不变，甲商品的件数是第一次的2倍；乙商品按原价销售，甲商品打折销售，第二次两种商品都销售完以后获得的总利润与第一次获得的总利润一样，求第二次甲商品是按原价打几折销售？【答案】(1)甲50件，乙115件(2)9折 【分析】（1）设第一次购进甲种商品x件，则购进乙种商品件，根据“第一次以4450元购进甲、乙两种商品”列方程求解即可；（2）设第二次甲商品是按原价打m折销售，根据“乙商品按原价销售，甲商品打折销售，第二次两种商品都销售完以后获得的总利润与第一次获得的总利润一样”列方程求解即可．【详解】（1）设第一次购进甲种商品x件，则购进乙种商品件，由题意得：解得所以，第一次购进甲种商品50件，则购进乙种商品115件．（2）设第二次甲商品是按原价打m折销售，根据题意得：解得答：第二次甲商品是按原价打9折销售．【点睛】本题考查了一元一次方程的应用，正确理解题意，找准等量关系是解题的关键．