

还剩21页未读,
继续阅读
(3)函数——2023年中考数学真题专项汇编
展开这是一份(3)函数——2023年中考数学真题专项汇编,共24页。
(3)函数——2023年中考数学真题专项汇编
1.【2023年天津】如图,要围一个矩形菜园ABCD,共中一边AD是墙,且AD的长不能超过26 m,其余的三边AB,BC,CD用篱笆,且这三边的和为40 m.有下列结论:
①AB的长可以为6 m;
②AB的长有两个不同的值满足菜园ABCD面积为;
③菜园ABCD面积的最大值为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
2.【2023年河南】如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为x,,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为( )
A.6 B.3 C. D.
3.【2023年安徽】下列函数中,y的值随x值的增大而减小的是( )
A. B. C. D.
4.【2023年山西】已知,,都在反比例函数的图象上,则a,b,c的大小关系用“<”连接的结果是( )
A. B. C. D.
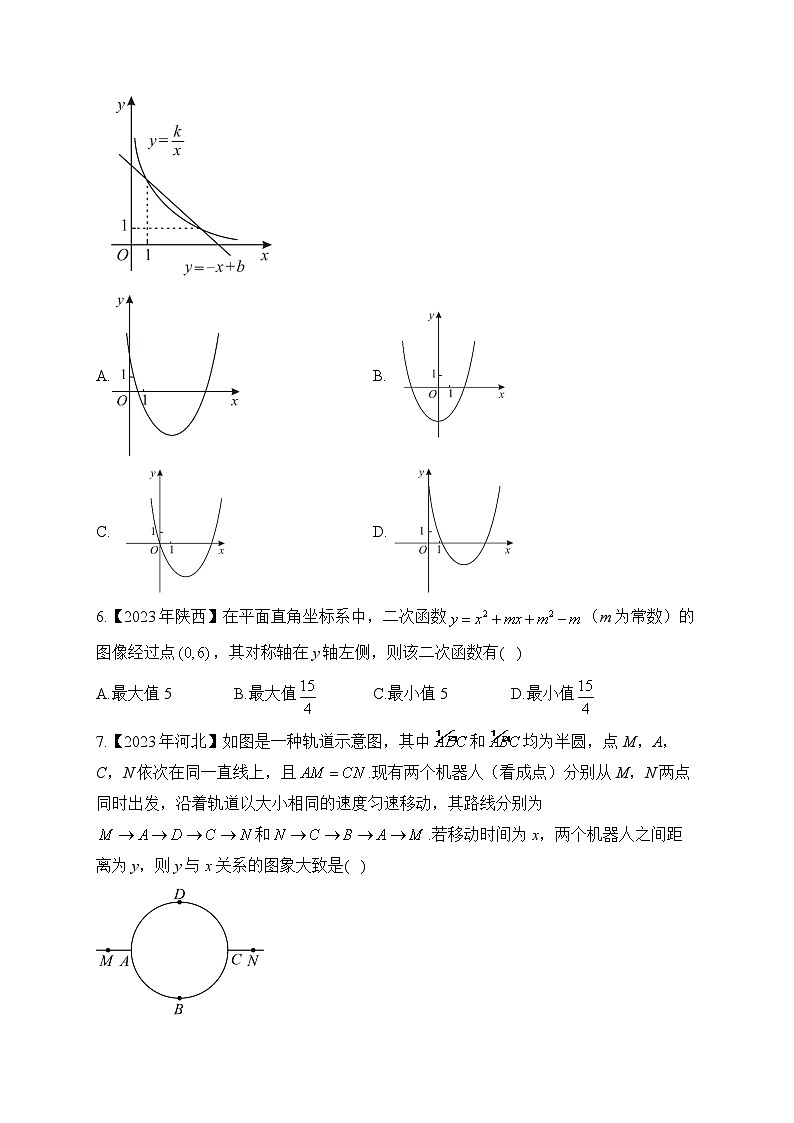
5.【2023年安徽】已知反比例函数在第一象限内的图象与一次函数的图象如图所示,则函数的图象可能为( )
A. B.
C. D.
6.【2023年陕西】在平面直角坐标系中,二次函数(m为常数)的图像经过点,其对称轴在y轴左侧,则该二次函数有( )
A.最大值5 B.最大值 C.最小值5 D.最小值
7.【2023年河北】如图是一种轨道示意图,其中和均为半圆,点M,A,C,N依次在同一直线上,且.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为和.若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( )
A. B.
C. D.
8.【2023年河北】已知二次函数和(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )
A.2 B. C.4 D.
9.【2023年天津】若直线向上平移3个单位长度后经过点,则m的值为________.
10.【2023年安徽】如图,O是坐标原点,的直角顶点A在轴的正半轴上,,,反比例函数的图象经过斜边OB的中点C.
(1)__________;
(2)D为该反比例函数图象上的一点,若,则的值为____________.
11.【2023年陕西A】如图,在矩形OABC和正方形CDEF中,点A在y轴正半轴上,点C,F均在x轴正半轴上,点D在边BC上,,.若点B,E在同一个反比例函数的图象上,则这个反比例函数的表达式是__________.
12.【2023年福建】已知抛物线经过,两点,若A,B分别位于抛物线对称轴的两侧,且,则n的取值范围是_________.
13.【2023年北京】在平面直角坐标系xOy中,,是抛物线上任意两点.设抛物线的对称轴为.
(1)若对于,有,求t的值;
(2)若对于,,都有,求t的取值范围.
14.【2023年天津】已知学生宿舍、文具店、体育场依次在同一条直线上,文具店离宿舍0.6 km,体育场离宿舍1.2 km,张强从宿舍出发,先用了10 min匀速跑步去体育场,在体育场锻炼了30 min,之后匀速步行了10 min到文具店买笔,在文具店停留10 min后,用了20 min匀速散步返回宿舍.下面图中x表示时间,y表示离宿舍的距离.图象反映了这个过程中张强离宿舍的距离与时间之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
张强离开宿舍的时间/min
1
10
20
60
张强离宿舍的距离/km
1.2
②填空:张强从体育场到文具店的速度为________;
③当时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
(2)当张强离开体育场15 min时,同宿舍的李明也从体育场出发匀速步行直接回宿舍,如果李明的速度为,那么他在回宿舍的途中遇到张强时离宿舍的距离是多少?(直接写出结果即可)
15.【2023年河南】小军借助反比例函数图象设计“鱼形”图案.如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作,连接BF.
(1)求k的值;
(2)求扇形AOC的半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
16.【2023年江西】如图,已知直线与反比例函数的图象交于点,与y轴交于点B,过点B作x轴的平行线交反比例函数的图象于点C.
(1)求直线AB和反比例函数图象的表达式;
(2)求的面积.
17.【2023年天津】已知抛物线(b,c为常数,)的顶点为P,与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,抛物线上的点M的横坐标为m,且,过点M作,垂足为N.
(1)若,.
①求点P和点A的坐标;
②当时,求点M的坐标;
(2)若点A的坐标为,且,当时,求点M的坐标.
18.【2023年重庆A】如图,在平面直角坐标系中,抛物线过点,且交x轴于点,B两点,交y轴于点C.
(1)求抛物线的表达式.
(2)点P是直线BC上方抛物线上的一动点,过点P作于点D,过点P作y轴的平行线交直线BC于点E,求周长的最大值及此时点P的坐标.
(3)在(2)中周长取得最大值的条件下,将该抛物线沿射线CB方向平移个单位长度,点M为平移后的抛物线的对称轴上一点.在平面内确定一点N,使得以点A,P,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
19.【2023年河南】小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网AB与y轴的水平距离,,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
20.【2023年安徽】在平面直角坐标系中,点O是坐标原点,抛物线经过点,对称轴为直线.
(1)求a,b的值;
(2)已知点B,C在抛物线上,点的横坐标为t,点C的横坐标为.过点B作x轴的垂线交直线OA于点D,过点C作x轴的垂线交直线OA于点E.
(ⅰ)当时,求与的面积之和;
(ⅱ)在抛物线对称轴右侧,是否存在点,使得以B,C,D,E为顶点的四边形的面积为?若存在,请求出B点的横坐标t的值;若不存在,请说明理由.
21.【2023年陕西A】某校想将新建图书楼的正门设计为一个抛物线型拱门,并要求所设计的拱门的跨度与拱高之积为,还要兼顾美观、大方,和谐、通畅等因素,设计部门按要求给出了两个设计方案.现把这两个方案中的拱门图形放入平面直角坐标系中,如图所示:
方案一,抛物线型拱门的跨度,拱高.其中,点N在x轴上,,.
方案二,抛物线型拱门的跨度,拱高.其中,点在x轴上,,.
要在拱门中设置高为的矩形框架,其面积越大越好(框架的粗细忽略不计).方案一中,矩形框架ABCD的面积记为,点A、D在抛物线上,边BC在ON上;方案二中,矩形框架的面积记为,点,在抛物线上,边在上.现知,小华已正确求出方案二中,当时,,请你根据以上提供的相关信息,解答下列问题:
(1)求方案一中抛物线的函数表达式;
(2)在方案一中,当时,求矩形框架ABCD的面积并比较,的大小.
22.【2023年山西】综合与研究
如图,二次函数的图象与x轴的正半轴交于点A,经过点A的直线与该函数图象交于点,与y轴交于点C.
(1)求直线AB的函数表达式及点C的坐标.
(2)点P是第一象限内二次函数图象上的一个动点,过点P作直线轴于点E,与直线AB交于点D,设点P的横坐标为m.
①当时,求m的值.
②当点P在直线AB上方时,连接OP,过点B作轴于点Q,BQ与OP交于点F,连接DF.设四边形FQED的面积为S,求S关于m的函数表达式,并求出S的最大值.
23.【2023年河北】在平面直角坐标系中,设计了点的两种移动方式:从点移动到点称为一次甲方式:从点移动到点称为一次乙方式.
例:点P从原点O出发连续移动2次;若都按甲方式,最终移动到点;若都按乙方式,最终移动到点;若按1次甲方式和1次乙方式,最终移动到点.
(1)设直线经过上例中的点M,N,求的解析式;并直接写出将向上平移9个单位长度得到的直线的解析式;
(2)点P从原点O出发连续移动10次,每次移动按甲方式或乙方式,最终移动到点.其中,按甲方式移动了m次.
①用含m的式子分别表示x,y;
②请说明:无论m怎样变化,点Q都在一条确定的直线上.设这条直线为,在图中直接画出的图象;
(3)在(1)和(2)中的直线,,上分别有一个动点A,B,C,横坐标依次为a,b,c,若A,B,C三点始终在一条直线上,直接写出此时a,b,c之间的关系式.
答案以及解析
1.答案:C
解析:设,则.由题意知,解得,AB的长不可以为6 m,故结论①不正确..令,整理,得,解得,,经检验,这两个根都符合题意,故结论②正确.,,当时,最大,最大值为200,故结论③正确.故选C.
2.答案:A
解析:当时,,此时,点P在线段BC的垂直平分线上运动.设点P运动的第一段路线的终点为O,如图,连接OC,则,.由函数图象可知,,,点O为等边三角形ABC的外心,,.过点O作于点F,则,,.故选A.
3.答案:D
解析:逐项分析如下.故选D.
选项
分析
是否符合题意
A
抛物线开口向上,当时,y随x增大而减小;当时,y随x增大而增大.
否
B
抛物线开口向下,当时,y随x增大而增大;当时,y随x增大而减小.
否
C
,y随x增大而增大.
否
D
,y随x增大而减小.
是
4.答案:D
解析:,反比例函数的图象位于第二、四象限,在每个象限内,y随x的增大而增大.,,,.
5.答案:A
解析:由反比例函数的图象可知,,故函数的图象与y轴交于正半轴,由此排除选项B,C.观察选项A,D,可知二者的一个区别在于当时y值的正负,此时.由题图可知,当时,反比例函数与一次函数的函数值相等,即,,对于函数,当时,、.故选A.
6.答案:D
解析:因为二次函数经过点,所以,解得,.因为该抛物线的对称轴在y轴的左侧,所以,所以.故该二次函数的表达式为.因为,所以该二次函数有最小值.
7.答案:D
解析:当两个机器人分别沿和沿运动时,y随x的增大而减小;当两个机器人分别沿和沿运动时,y等于圆的直径;当两个机器人分别沿和沿运动时,y随x的增大而增大.故选D.
8.答案:A
解析:对于函数,当时,,,抛物线与x轴的交点坐标分别为,,其对称轴为直线.对于函数,当时,,,抛物线与x轴的交点坐标分别为,,其对称轴为直线.这两个函数的图象与x轴都有两个交点,.当时,这四个交点中每相邻两点间的距离都相等,,解得(舍去),,这两个函数图象对称轴之间的距离为2.当时,同理可求得这两个函数图象对称轴之间的距离也为2.
9.答案:5
解析:平移后的直线的解析式为,将代入,得.
10.答案:(1)
(2)4
解析:(1)在中,,,则,,.点C是OB的中点,,.
(2)由(1)可知,结合,利用待定系数法计算可得直线AC的解析式为.,,直线BD可看成是直线AC向上平移2个单位长度得到的,直线BD的解析式为.联立直线BD与反比例函数的解析式,得,整理,得,解得,,,,.
11.答案:
解析:设,则点,点,点B,E在同一个反比例函数的图象上,,.,该反比例函数的表达式为.
12.答案:
解析:(第一步:求出抛物线的对称轴.)
对于抛物线,对称轴为直线.
(第二步:分两种情况讨论.)
若点A,B分别位于抛物线对称轴的两侧,则分点A在对称轴左侧,点B在对称轴右侧和点A在对称轴右侧,点B在对称轴左侧两种情况讨论.当点A在对称轴左侧,点B在对称轴右侧时,,,此时n不存在.当点A在对称轴右侧,点B在对称轴左侧时,,,此时.由可知,点B到抛物线的对称轴的距离更远,,,.
(第三步:归纳总结.)
综上,n的取值范围为.
13.答案:(1)
(2)
解析:(1)当,时,,
抛物线的对称轴为直线,
.
(2),抛物线开口向上,
抛物线上离对称轴越远的点纵坐标越大.
又,抛物线的对称轴为直线,
点M到直线的距离小于点N到直线的距离.
由题意知点M在点N左侧.
连接MN,则MN中点的横坐标为.
由可知MN的中点在直线的右侧,.
,,,,
.
14.答案:(1)①从左到右依次填:0.12 1.2 0.6
②0.06
③当时,;
当时,.
(2)0.3 km
解析:(1)略
(2)由题意可知,当时,李明离开体育场,
当时,李明回到宿舍.
当时,设李明离开宿舍的距离与时间x的函数关系式为,
将,分别代入,可求得,,
.
由题意易知李明在回宿舍的途中遇到张强时,.
令,解得.当时,,
李明在回宿舍的途中遇到张强时离宿舍的距离是0.3 km.
15.答案:(1)
(2)
(3)
解析:(1)点在反比例函数的图象上,.
(2)如图,连接AC交OD于点G.
四边形AOCD为菱形,,.
点A的坐标为,,,
,,
,.
综上,扇形AOC的半径为2,圆心角的度数为60°.
(3)设OE,BF交于点N,四边形OBEF是菱形,
,,.
又,
.
16.答案:(1)直线AB的表达式为,反比例函数图象的表达式为
(2)
解析:(1)直线与反比例函数的图象交于点,
,,
,,
直线AB的表达式为,反比例函数图象的表达式为.
(2)易得.
轴,
C点的纵坐标为1,BC与x轴的距离为1.
令,得,.
如图,过点A作于点D,
则,
.
17.答案:(1)①;②
(2)
解析:(1)①由,,得抛物线的解析式为。
,点P的坐标为.
当时,,解得,.
又点A在点B的左侧,点A得坐标为.
②过点M作轴于点E,与直线AC相交于点F.易得点.
又点,,在中,,
在中,.
抛物线上的点M的横坐标为m,其中,
点,点,
,,
.
在中,易得,.
又,,即,解得,(舍去),
点M的坐标为.
(2)点在抛物线上,其中,
,得,抛物线的解析式为,
点,其中.
,
顶点P的坐标为,对称轴为直线.
过点M作于点Q,则,点.
由,得,于是,
,
整理,得,解得,(舍去),
点.
同(1),过点M作轴于点E,与直线AC相交于点F,
则点,点.
,
,
即,解得,(舍去),
点M的坐标为.
18.答案:(1)
(2)
(3)见解析
(1)把,分别代入中,
得解得
故该抛物线的表达式为.
(2)由(1)易得,,,,.
根据直线BC过点,,易得直线BC的表达式为.
轴,.又,,
,,,.
设,,则,
,
,当时,PE有最大值2,
周长的最大值是,
此时点P的坐标为.
(3)满足条件的点N的坐标为,或.
抛物线沿射线CB方向平移个单位长度,即抛物线向右平移2个单位长度,向下平移1个单位长度,
平移后的抛物线的对称轴为直线.
设,,
①当AP为菱形的对角线时,
由题意得,即,
解得,,,,
,,.
②当AP为菱形的边时,若,则,
解得,,,,
,,或.
若,则,此方程无解.
(注:写出点N的一种情况的求解过程即可)
19.答案:(1)-0.4
(2)选择吊球,使球的落地点到C点的距离更近
解析:(1)依题意知,点P为直线与y轴的交点.
当时,,点P的坐标为.
抛物线经过点P,,解得.
(2),,.
若选择扣球,当时,得,解得,
此时,球的落地点到C点的距离为.
若选择吊球,由(1)知,.
当时,得,解得,(舍),
此时球的落地点到C点的距离为.
,应选择吊球.
20.答案:(1),
(2)(ⅰ)2
(ⅱ)存在,
解析:(1)抛物线的对称轴为直线,,.
将代入,得,
解得,.
(2)(ⅰ)如图(1),易知直线OA的解析式为.
由题意可知,,,,
,,
,
,
.
(ⅱ)存在.
过点D作于点H,则.
分以下2种情况讨论.
①当时,如图(2),易知四边形DCEB为梯形,
此时,,,
.
令,解得.
②当时,如图(3),易知四边形DBCE为梯形,
此时,,,
.
令,解得(舍),(舍).
综上所述,t的值为.
21.答案:(1)
(2)
解析:(1)由题意知,方案一中抛物线的顶点为,
设,且该抛物线经过点,
解得,.
(2)令,则,
解得,,,
,而,.
22.答案:(1)(2)①2,3或;②
解析:(1)对于,当时,,
解得,.
点A在x轴正半轴上,点A的坐标为.
设直线AB的函数表达式为.
将A,B两点的坐标,分别代入,
得解得直线AB的函数表达式为.
将代入,得,点C的坐标为.
(2)①点P在第一象限内二次函数的图象上,
且轴于点E,与直线AB交于点D,其横坐标为m,
点P,D的坐标分别为,,
,,.
点C的坐标为,.
,.
如图(1),当点P在直线AB上方时,
.
,,解得,.
如图(2),当点P在直线AB下方时,
.
,,解得.
,.
综上所述,m的值为2,3或.
②如图(3),由①得,,,.
轴于点Q,交OP与点F,点B的坐标为,
,.
点P在直线AB上方,.
轴于点E,.,
,,,
,,四边形FQED为平行四边形.
又轴,四边形FQED为矩形,
,即.
,,,
当时,S取最大值,最大值为.
23.答案:(1)直线的解析式为;将直线向上平移9个单位长度得到的直线的解析式为
(2)①,
②见解析
(3)
解析:(1)设直线的解析式为,
把,分别代入,
得解得
直线的解析式为.
将直线向上平移9个单位长度得到的直线的解析式为.
(2)①点P从原点O出发连续移动10次,按照甲方式移动了m次,
点P按照乙方式移动了次,
,.
②由①知,,,
,,
无论m怎么变化,点Q都在直线上.
直线的图象如图所示.
(3)a,b,c之间的关系式为.
解析:点A,B,C的横坐标分别为a,b,c,且分别在直线,,上,
,,.
设直线AB的解析式为,
把点A,B的坐标分别代入,
得
解得
直线AB的解析式为.
A,B,C三点始终在一条直线上,
,
整理,得.
相关试卷
2021年中考数学真题汇编:二次函数专项复习解析版:
这是一份2021年中考数学真题汇编:二次函数专项复习解析版,共59页。
2023年黑龙江省中考数学真题分类汇编3 函数:
这是一份2023年黑龙江省中考数学真题分类汇编3 函数,共51页。试卷主要包含了选择题,填空题,综合题,实践探究题等内容,欢迎下载使用。
(3)函数——2023年中考数学真题专项汇编:
这是一份(3)函数——2023年中考数学真题专项汇编,共24页。








