2008年山东省潍坊市中考数学试题及答案

2008年山东省潍坊市中考数学真题

第Ⅰ卷  选择题(共36分)

一、选择题(本题共12小题，每小题3分，满分36分)

1. 下列运算正确的是(     )

A．x5-x3=x2    B．x4(x3)2=x10   C．(-x)12÷(-x)3=x9  D．(-2x)3·x-3=8

2. 下列方程有实数解的是(    )

A．=1     B．|x+1|+2=0     C．=     D．x2-2x+3=0

3. 如图，矩形ABCD中，AD∥BC，AD=AB，BC=BD，∠A=100°，则∠C= (    )

A．80°       B．70°        C．75°        D．60°

4. 若(a+)2与|b-1|互为相反数，则的值为(    )

A．       B．+1       C．-1       D．1-

5. 
   
   某蓄水池的横断面示意图如右图，分深水区和浅水区，如果这个注满水的蓄水池以固定的流量把水全部放出．下面的图象能大致表示水的深度h和放水时间t之间的关系的是(    )
6. 如图，Rt△ABC中，AB⊥AC，AB=3，AC=4，P是BC上一点，作PE⊥AB于E，PD⊥AC于D，设BP=x，则PD+PE=(     )

A．+3       B．4-       C．       D．-

7. 时代中学周末有40人去体育场观看足球比赛，40张票分别为B区第2排1号到40号．分票采用随机抽取的办法，小明第一个抽取，他抽取的座号为10号，接着小亮从其余的票中任意抽取一张，取得的一张恰与小明邻座的概率是(    )

A．           B．            C．            D．

8. 如图，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E， EF∥AC，下列结论一定成立的是(    )

A．AB=BF     B．AE=ED     C．AD=DC     D．∠ABE=∠DFE

第8题图            第10题图              第11题图                  第15题图

9. 如图，△ABC内接于圆O，∠A=50°，∠ABC=60°，BD是圆O的直径， BD交AC于点E，连结DC，则∠AEB等于(    )

A．70°            B．110°            C．90°            D．120°

10. 已知反比例函数y=，当x>0时，y随x的增大而增大，则关于x的方程ax2-2x+b=0的根的情况是(    )

A. 有两个正根     B. 有两个负根     C. 有一个正根一个负根     D.没有实数根

11. 在平行四边形ABCD中，点A1，A2，A3，A4和C1，C2，C3，C4分别是AB和CD的五等分点，点B1，B2和D1，D2分别是BC和DA的三等分点，已知四边形A4B2C4D2的面积为1，则平行四边形ABCD的面积为(    )

A．2                 B．                 C．                 D．15

12. 若一次函数y=(m+1)x+m的图象过第一、三、四象限，则函数y=mx2-mx (    )

A．有最大值     B．有最大值-     C．有最小值     D．有最小值-

第Ⅱ卷  非选择题(共84分)

二、填空题(本题共5小题，每小题3分，共15分)

13. 分解因式：x3+6x2-27x=                         
14. 已知3x+4≤6+2(x-2)，则|x+1|的最小值等于                
15. 如图，正六边形内接于圆O，圆O的半径为10，则圆中阴影部分的面积为           
16. 下列每个图是由若干个圆点组成的形如四边形的图案，当每条边(包括顶点)上有n(n≥2)个圆点时，图案的圆点数为Sn．按此规律推断Sn关于n的关系式为：                 ．

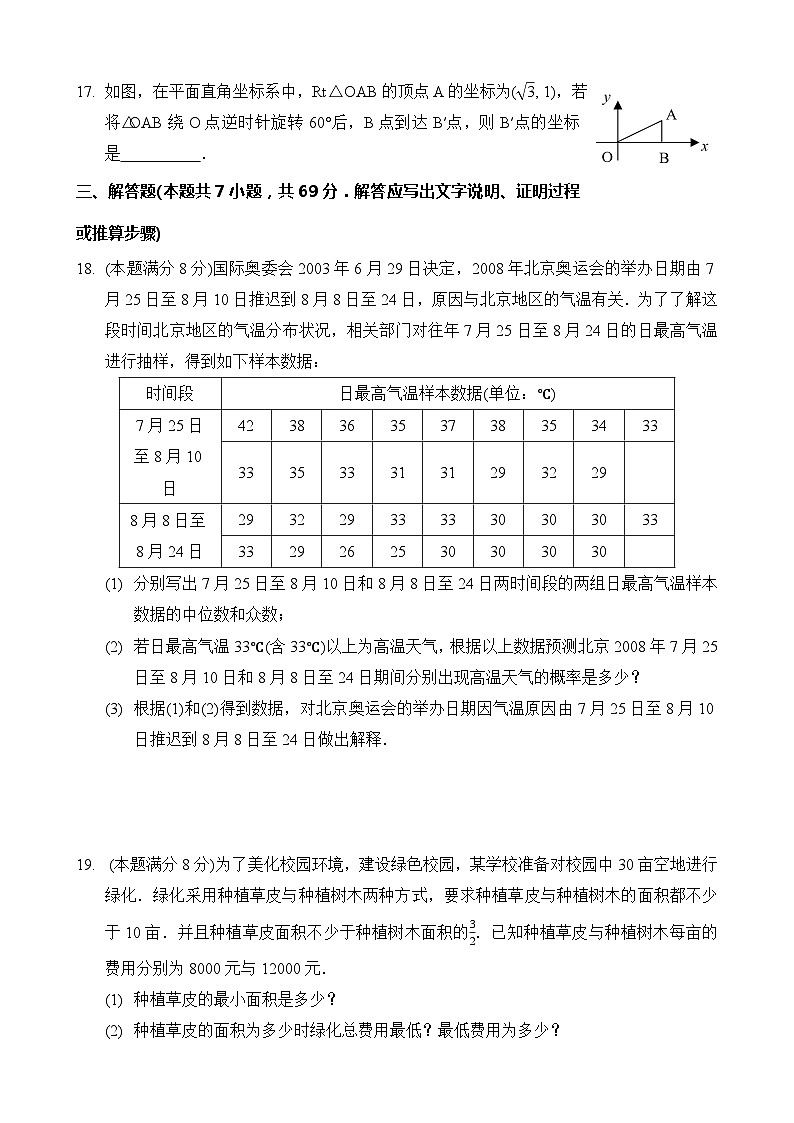
17. 如图，在平面直角坐标系中，Rt△OAB的顶点A的坐标为(, 1)，若将△OAB绕O点逆时针旋转60°后，B点到达B′点，则B′点的坐标是          ．

三、解答题(本题共7小题，共69分．解答应写出文字说明、证明过程或推算步骤)

18. (本题满分8分)国际奥委会2003年6月29日决定，2008年北京奥运会的举办日期由7月25日至8月10日推迟到8月8日至24日，原因与北京地区的气温有关．为了了解这段时间北京地区的气温分布状况，相关部门对往年7月25日至8月24日的日最高气温进行抽样，得到如下样本数据：

(1)     分别写出7月25日至8月10日和8月8日至24日两时间段的两组日最高气温样本数据的中位数和众数；

(2)     若日最高气温33℃(含33℃)以上为高温天气，根据以上数据预测北京2008年7月25日至8月10日和8月8日至24日期间分别出现高温天气的概率是多少？

(3)     根据(1)和(2)得到数据，对北京奥运会的举办日期因气温原因由7月25日至8月10日推迟到8月8日至24日做出解释．

19.  (本题满分8分)为了美化校园环境，建设绿色校园，某学校准备对校园中30亩空地进行绿化．绿化采用种植草皮与种植树木两种方式，要求种植草皮与种植树木的面积都不少于10亩．并且种植草皮面积不少于种植树木面积的．已知种植草皮与种植树木每亩的费用分别为8000元与12000元．

(1)     种植草皮的最小面积是多少？

(2)     种植草皮的面积为多少时绿化总费用最低？最低费用为多少？

20. (本题满分9分)如图，AC是圆O的直径，AC=10厘米，PA、PB是圆O的切线，A、B为切点．过A作AD⊥BP，交BP于D点，连结AB、BC．

(1)     求证：△ABC∽△ADB；

(2)    
若切线AP的长为12厘米，求弦AB的长．

21. (本题满分10分)如图，ABCD为平行四边形，AD=a，BE∥AC，DE交AC的延长线于F点，交BE于E点．

(1)     求证：DF=FE；

(2)     若AC=2CF，∠ADC=60°，AC⊥DC，求BE的长；

(3)    
在(2)的条件下，求四边形ABED的面积．

22. (本题满分11分)一家化工厂原来每月利润为120万元．从今年一月起安装使用回收净化设备(安装时间不计)，一方面改善了环境，另一方面大大降低原料成本．据测算，使用回收净化设备后的1至x月(1≤x≤12)的利润的月平均值w(万元)满足w=10x+90，第2年的月利润稳定在第1年的第12个月的水平．

(1)     设使用回收净化设备后的1至x月(1≤x≤12)的利润和为y，写出y关于x的函数关系式，并求前几个月的利润和等于700万元？

(2)     当x为何值时，使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等？

(3)     求使用回收净化设备后两年的利润总和．

23. (本题满分11分)如图，矩形纸片ABCD中，AB=8，将纸片折叠，使顶点B落在边AD的E点上，折痕的一端G点在边BC上，BG=10．

(1)     当折痕的另一端F在AB边上时，如图(1)，求△EFG的面积；

(2)    
当折痕的另一端F在AD边上时，如图(2)，证明四边形BGEF为菱形，并求出折痕GF的长．

24. (本题满分12分)如图，圆B切y轴于原点O，过定点A(-2, 0)作圆B切线交圆于点P．已知tan∠PAB=，抛物线C经过A、P两点．

(1)     求圆B的半径；

(2)     若抛物线C经过点B，求其解析式；

(3)    
投抛物线C交y轴于点M，若三角形APM为直角三角形，求点M的坐标．

参考答案：

一、1 B  2 C  3 C  4 B  5 A  6 ？  7 D  8 A   9 B  10 C    11 C   12 ？ 

二、13.x(x-3)(x+9); 14.1; 15.100-150; 16. Sn =4(n-1); 17. ;

18.(1)中位数：34，众数：33和35；(将所给数据按顺序排列，中间的一个数是中位数，出现次数最多的数是众数)

(2)70.6%，23.5%；(用高温天气的天数除以总天数)

(3)7月25日至8月10日70.6%是高温天气，8月8日至24日23.5%是高温天气，高温天气不适宜进行剧烈的体育活动，故北京奥运会的举办日期因气温原因由7月25日至8月10日推迟至8月8日至24日是非常合理的。

19.(1)解设种植草皮的面积为x亩，则种植树木面积为(30-x)亩，则：

解得

答：种植草皮的最小面积是18亩。

(2)由题意得：y=8000x+12000(30-x)=360000-4000x，当x=20时y有最小值280000元

20.(1)证明：∵AC是圆O的直径，∴∠ABC=90 o，

又∵AD⊥BP，∴∠ADB=90 o，∴∠ABC=∠ADB，

又∵PB是圆的切线，∴∠ABD=∠ACB，

在△ABC和△ADB中：

，∴△ABC∽△ADB;

(2)连结OP,在Rt△AOP中，AP=12厘米,OA=5厘米,根据勾股定理求得OP=13厘米,又由已知可证得△ABC∽△PAO, ∴,得,解得AB=厘米.

21.(1)证明：延长DC交BE于点M，∵BE∥AC，AB∥DC,∴四边形ABMC是平行四边形，

∴CM=AB=DC,C为DM的中点，BE∥AC，DF=FE;

(2)由(2)得CF是△DME的中位线，故ME=2CF,又∵AC=2CF，四边形ABMC是平行四边形，∴BE=2BM=2ME=2AC, 又∵AC⊥DC, ∴在Rt△ADC中利用勾股定理得AC=

, ∴=.

(3)可将四边形ABED的面积分为两部分，梯形ABMD和三角形DME,在Rt△ADC中利用勾股定理得DC=,由CF是△DME的中位线得CM=DC=,四边形ABMC是平行四边形得AM=MC=,BM=AC=,∴梯形ABMD面积为：;由AC⊥DC和BE∥AC可证得三角形DME是直角三角形，其面积为：,∴四边形ABED的面积为+

22. 解：(1)y=xw=x(10x+90)=10x2+90x, 10x2+90x=700,解得x=5

答：前5个月的利润和等于700万元

(2)10x2+90x=120x,解得，x=3

答：当x为3时，使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等.

(3)12(10×12+90)+12(10×12+90)=5040(万元)

23.(本题满分11分)如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10.

(1)当折痕的另一端F在AB边上时,如图(1).求△EFG的面积.

(2)当折痕的另一端F在AD边上时,如图(2).证明四边形BGEF为菱形,并求出折痕GF的长.

解:(1)过点G作GH⊥AD,则四边形ABGH为矩形,∴GH=AB=8,AH=BG=10,由图形的折叠可知△BFG≌△EFG,∴EG=BG=10,∠FEG=∠B=90°；∴EH=6,AE=4,∠AEF+∠HEG=90°,∵∠AEF+∠AFE=90°,∴∠HEG=∠AFE,又∵∠EHG=∠A=90°,∴△EAF∽△EHG,∴,∴EF=5,∴S△EFG=EF·EG=×5×10=25.

(2)由图形的折叠可知四边形ABGF≌四边形HEGF,∴BG=EG,AB=EH,

∠BGF=∠EGF,∵EF∥BG，∴∠BGF=∠EFG,∴∠EGF =∠EFG,∴EF=EG,

∴BG=EF,∴四边形BGEF为平行四边形,又∵EF=EG,∴平行四边形BGEF为菱形；

连结BE，BE、FG互相垂直平分，在Rt△EFH中,EF=BG=10,EH=AB=8,由勾股定理可得FH=AF=6，∴AE=16，∴BE==8，∴BO=4，∴FG=2OG=2=4。

24. (1) 2  (2) y=-x2+4   (3) (0, -6)或(0, 6)或(0, )或(0, )