中考数学一轮复习考点复习专题15 函数与行程问题【考点精讲】(含解析)
展开
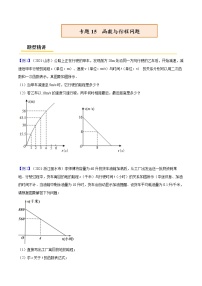
【例1】(2021·山东)公路上正在行驶的甲车,发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s) 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至9m/s时,它行驶的路程是多少?
(2)若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?
【答案】(1)87.5m;(2)6秒时两车相距最近,最近距离是2米
【分析】
(1)根据图像分别求出一次函数和二次函数解析式,令v=9求出t,代入求出s即可;
(2)分析得出当v=10m/s时,两车之间距离最小,代入计算即可.
【详解】
解:(1)由图可知:二次函数图像经过原点,
设二次函数表达式为,一次函数表达式为,
∵一次函数经过(0,16),(8,8),
则,解得:,
∴一次函数表达式为,
令v=9,则t=7,
∴当t=7时,速度为9m/s,
∵二次函数经过(2,30),(4,56),
则,解得:,
∴二次函数表达式为,
令t=7,则s==87.5,
∴当甲车减速至9m/s时,它行驶的路程是87.5m;
(2)∵当t=0时,甲车的速度为16m/s,
∴当10<v<16时,两车之间的距离逐渐变小,
当0<v<10时,两车之间的距离逐渐变大,
∴当v=10m/s时,两车之间距离最小,
将v=10代入中,得t=6,
将t=6代入中,得,
此时两车之间的距离为:10×6+20-78=2m,
∴6秒时两车相距最近,最近距离是2米.
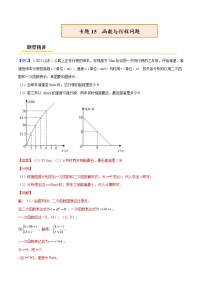
【例2】(2021·浙江丽水市)李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出工厂离目的地的路程;
(2)求s关于t的函数表达式;
(3)当货车显示加油提醒后,问行驶时间t在怎样的范围内货车应进站加油?
【答案】(1)工厂离目的地的路程为880千米;(2);(3).
【分析】
(1)根据图象直接得出结论即可;
(2)根据图象,利用待定系数法求解函数表达式即可;再求出油量为
(3)分别求出余油量为10升和0升时行驶的路程,根据函数表达式求出此时的t值,即可求得t的范围.
【详解】
解:(1)由图象,得时,,
答:工厂离目的地的路程为880千米.
(2)设,将和分别代入表达式,
得,解得,
∴s关于t的函数表达式为.
(3)当油箱中剩余油量为10升时,(千米),
,解得(小时).
当油箱中剩余油量为0升时,(千米),
,解得(小时).
随t的增大而减小,
的取值范围是.
【例3】(2021·天津)在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知学校、书店、陈列馆依次在同一条直线上,书店离学校,陈列馆离学校.李华从学校出发,匀速骑行到达书店;在书店停留后,匀速骑行到达陈列馆;在陈列馆参观学习一段时间,然后回学校;回学校途中,匀速骑行后减速,继续匀速骑行回到学校.给出的图象反映了这个过程中李华离学校的距离与离开学校的时间之间的对应关系.
请根据相关信息,解答下列问题:
(Ⅰ)填表
离开学校的时间/ | |||||
离学校的距离/ |
|
|
|
(Ⅱ)填空:
①书店到陈列馆的距离为________;
②李华在陈列馆参观学的时间为_______h;
③李华从陈列馆回学校途中,减速前的骑行速度为______;
④当李华离学校的距离为时,他离开学校的时间为_______h.
(Ⅲ)当时,请直接写出y关于x的函数解析式.
【答案】(Ⅰ)10,12,20;(Ⅱ)①8;②3;③28;④或;(Ⅲ)当时,;当时,;当时,.
【分析】
(Ⅰ)根据函数图象,利用待定系数法,分段写出函数解析式,根据表格中x,代入相应的解析式,得到y;
(Ⅱ)①根据图象进行分析即可;
②根据图象进行分析即可;
③根据时的函数解析式可求;
④分和两种情况讨论,将距离为4km代入相应的解析式求出时间x;
(Ⅲ)根据函数图象,利用待定系数法,分段写出函数解析式即可.
【详解】
对函数图象进行分析:
①当时,设函数关系式为,由图象可知,当x=0.6时,y=12,
则,解得
∴当时,设函数关系式为
②由图象可知,当时,
③当时,设函数关系式为,由图象可知,当x=1时,y=12;当x=1.5时,y=20,
则 ,解得
∴当时,设函数关系式为
④由图象可知,当时,
⑤当时,设函数关系式为,由图象可知,当x=4.5时,y=20;当x=5时,y=6,
则,解得
∴当时,设函数关系式为
⑥当时,设函数关系式为,由图象可知,当x=5时,y=6;当x=5.5时,y=0,
则,解得
∴当时,设函数关系式为
(Ⅰ)∵当时,函数关系式为
∴当x=0.5时,.故第一空为10.
当时,.故第二空为12.
当时,.故第二空为20.
(Ⅱ)①李华从学校出发,匀速骑行到达书店;在书店停留后,匀速骑行到达陈列馆.由图象可知书店到陈列馆的距离;
②李华在陈列馆参观学习一段时间,然后回学校.由图象可知李华在陈列馆参观学的时间;
③当时,设函数关系式为,所以李华从陈列馆回学校途中,减速前的骑行速度为28;
④当李华离学校的距离为时,或
由上对图象的分析可知:
当时,设函数关系式为
令,解得
当时,设函数关系式为
令,解得
∴当李华离学校的距离为时,他离开学校的时间为或.
(Ⅲ)由上对图象的分析可知:
当时,;
当时,;
当时,.
1.(2021·陕西)在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回“鼠”、“猫”距起点的距离与时间之间的关系如图所示.
(1)在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是______;
(2)求的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.
【答案】(1)1;(2);(3)
【分析】
(1)根据图象得到“猫”追上“鼠”时的路程与它们的用时,再求平均速度差即可;
(2)找出A点和B点坐标,运用待定系数法求出直线AB的解析式即可;
(3)令,求出的值,再减去1即可得解.
【详解】
解:(1)从图象可以看出“猫”追上“鼠”时,行驶距离为30米,“鼠”用时6min,“猫”用时(6-1)=5min,
所以,“猫”的平均速度与“鼠”的平均速度的差是
故答案为:1;
(2)由图象知,A(7,30),B(10,18)
设的表达式,
把点A、B代入解析式得,
解得,
∴.
(3)令,则.
∴.
14.5-1=13.5(min)
∴“猫”从起点出发到返回至起点所用的时间为.
2.(2021·甘肃武威市)如图1,小刚家,学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离与他所用的时间的函数关系如图2所示.
(1)小刚家与学校的距离为___________,小刚骑自行车的速度为________;
(2)求小刚从图书馆返回家的过程中,与的函数表达式;
(3)小刚出发35分钟时,他离家有多远?
【答案】(1)3000,200;(2);(3)
【分析】
(1)从起点处为学校出发去处为图书馆,可求小刚家与学校的距离为3000m,小刚骑自行车匀速行驶10分钟,从3000m走到5000m可求骑自行车的速度即可;
(2)求出从图书馆出发时的时间与路程和回到家是的时间与路程,利用待定系数法求解析式即可;
(3)小刚出发35分钟,在返回家的时间内,利用函数解析式求出当时,函数值即可.
【详解】
解:(1)小刚骑自行车匀速从学校到图书馆,从起点3000m处为学校出发去5000m处为图书馆,
∴小刚家与学校的距离为3000m,
小刚骑自行车匀速行驶10分钟,从3000m走到5000m,
行驶的路程为5000-3000=2000m,
骑自行车的速度为2000÷10=200m/min,
故答案为:3000,200;
(2)小刚从图书馆返回家的时间:.
总时间:.
设返回时与的函数表达式为,
把代入得:,
解得,,
.
(3)小刚出发35分钟,即当时,
,
答:此时他离家.
3.(2020•黑龙江)为抗击疫情,支持武汉,某物流公司的快递车和货车每天往返于物流公司、武汉两地,快递车比货车多往返一趟,如图表示两车离物流公司的距离y(单位:千米)与快递车所用时间x(单位:时)的函数图象,已知货车比快递车早1小时出发,到达武汉后用2小时装卸货物,按原速、原路返回,货车比快递车最后一次返回物流公司晚1小时.
(1)求ME的函数解析式;
(2)求快递车第二次往返过程中,与货车相遇的时间.
(3)求两车最后一次相遇时离武汉的距离.(直接写出答案)
【分析】(1)利用待定系数法求一次函数解析式即可;
(2)利用待定系数法分别求出BC与FG的解析式,再联立解答即可;
(3)根据题意列式计算即可.
【解析】(1)设ME的函数解析式为y=kx+b(k≠0),由ME经过(0,50),(3,200)可得:
,解得,
∴ME的解析式为y=50x+50;
(2)设BC的函数解析式为y=mx+n,由BC经过(4,0),(6,200)可得:
,解得,
∴BC的函数解析式为y=100x﹣400;
设FG的函数解析式为y=px+q,由FG经过(5,200),(9,0)可得:
,解得,
∴FG的函数解析式为y=﹣50x+450,
解方程组得,
同理可得x=7h,
答:货车返回时与快递车图中相遇的时间h,7h;
(3)(9﹣7)×50=100(km),
答:两车最后一次相遇时离武汉的距离为100km.
4.(2020•天津)在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍0.7km,图书馆离宿舍1km.周末,小亮从宿舍出发,匀速走了7min到食堂;在食堂停留16min吃早餐后,匀速走了5min到图书馆;在图书馆停留30min借书后,匀速走了10min返回宿舍.给出的图象反映了这个过程中小亮离宿舍的距离ykm与离开宿舍的时间xmin之间的对应关系.
请根据相关信息,解答下列问题:
(Ⅰ)填表:
离开宿舍的时间/min | 2 | 5 | 20 | 23 | 30 |
离宿舍的距离/km | 0.2 |
| 0.7 |
|
|
(Ⅱ)填空:
①食堂到图书馆的距离为 km;
②小亮从食堂到图书馆的速度为 km/min;
③小亮从图书馆返回宿舍的速度为 km/min;
④当小亮离宿舍的距离为0.6km时,他离开宿舍的时间为 min.
(Ⅲ)当0≤x≤28时,请直接写出y关于x的函数解析式.
【分析】(Ⅰ)根据题意和函数图象,可以将表格补充完整;
(Ⅱ)根据函数图象中的数据,可以将各个小题中的空补充完整;
(Ⅲ)根据(Ⅱ)中的结果和函数图象中的数据,可以写出当0≤x≤28时,y关于x的函数解析式.
【解析】(Ⅰ)由图象可得,
在前7分钟的速度为0.7÷7=0.1(km/min),
故当x=2时,离宿舍的距离为0.1×2=0.2(km),
在7≤x≤23时,距离不变,都是0.7km,故当x=23时,离宿舍的距离为0.7km,
在28≤x≤58时,距离不变,都是1km,故当x=30时,离宿舍的距离为1km,
故答案为:0.2,0.7,1;
(Ⅱ)由图象可得,
①食堂到图书馆的距离为1﹣0.7=0.3(km),
故答案为:0.3;
②小亮从食堂到图书馆的速度为:0.3÷(28﹣23)=0.06(km/min),
故答案为:0.06;
③小亮从图书馆返回宿舍的速度为:1÷(68﹣58)=0.1(km/min),
故答案为:0.1;
④当0≤x≤7时,
小亮离宿舍的距离为0.6km时,他离开宿舍的时间为0.6÷0.1=6(min),
当58≤x≤68时,
小亮离宿舍的距离为0.6km时,他离开宿舍的时间为(1﹣0.6)÷0.1+58=62(min),
故答案为:6或62;
(Ⅲ)由图象可得,
当0≤x≤7时,y=0.1x;
当7<x≤23时,y=0.7;
当23<x≤28时,设y=kx+b,
,得,
即当23<x≤28时,y=0.06x﹣0.68;
由上可得,当0≤x≤28时,y关于x的函数解析式是y.
5.(2020•淮安)甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后.按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发x小时后离甲地的路程为y千米,图中折线OCDE表示接到通知前y与x之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为 千米/小时;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.
【分析】(1)观察图象即可得出休息前汽车行驶的速度;
(2)根据题意求出点E的横坐标,再利用待定系数法解答即可;
(3)求出到达乙地所行驶的时间即可解答.
【解析】(1)由图象可知,休息前汽车行驶的速度为80千米/小时;
故答案为:80;
(2)休息后按原速继续前进行驶的时间为:(240﹣80)÷80=(小时),
∴点E的坐标为(3.5,240),
设线段DE所表示的y与x之间的函数表达式为y=kx+b,则:
,解得,
∴线段DE所表示的y与x之间的函数表达式为80x﹣40;
(3)接到通知后,汽车仍按原速行驶,则全程所需时间为:290÷80+0.5=4.125(小时),
12:00﹣8:00=4(小时),
4.125>4,
所以接到通知后,汽车仍按原速行驶不能准时到达.
6.(2020•齐齐哈尔)团结奋战,众志成城,齐齐哈尔市组织援助医疗队,分别乘甲、乙两车同时出发,沿同一路线赶往绥芬河.齐齐哈尔距绥芬河的路程为800km,在行驶过程中乙车速度始终保持80km/h,甲车先以一定速度行驶了500km,用时5h,然后再以乙车的速度行驶,直至到达绥芬河(加油、休息时间忽略不计).甲、乙两车离齐齐哈尔的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题:
(1)甲车改变速度前的速度是 km/h,乙车行驶 h到达绥芬河;
(2)求甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式,不用写出自变量x的取值范围;
(3)甲车到达绥芬河时,乙车距绥芬河的路程还有 km;出发 h时,甲、乙两车第一次相距40km.
【分析】(1)结合图象,根据“速度=路程÷时间”即可得出甲车改变速度前的速度;根据“时间=路程÷速度”即可得出乙车行驶的时间;
(2)根据题意求出甲车到达绥芬河的时间,再根据待定系数法解答即可;
(3)根据甲车到达绥芬河的时间即可求出甲车到达绥芬河时,乙车距绥芬河的路程;根据“路程差=速度差×时间”列式计算即可得出甲、乙两车第一次相距40km行驶的时间.
【解析】(1)甲车改变速度前的速度为:500出5=100(km/h),乙车达绥芬河是时间为:800÷80=10(h),
故答案为:100;10;
(2)∵乙车速度为80km/h,
∴甲车到达绥芬河的时间为:,
甲车改变速度后,到达绥芬河前,设所求函数解析式为:y=kx+b(k≠0),
将(5,500)和(,800)代入得:,
解得,
∴y=80x+100,
答:甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式为y=80x+100();
(3)甲车到达绥芬河时,乙车距绥芬河的路程为:800﹣80100(km),
40÷(100﹣80)=2(h),
即出发2h时,甲、乙两车第一次相距40km.
故答案为:100;2.
中考数学一轮复习考点复习专题22 函数与公共点问题【考点精讲】(含解析): 这是一份中考数学一轮复习考点复习专题22 函数与公共点问题【考点精讲】(含解析),共23页。
中考数学一轮复习考点复习专题19 函数与角度有关问题【考点精讲】(含解析): 这是一份中考数学一轮复习考点复习专题19 函数与角度有关问题【考点精讲】(含解析),共60页。试卷主要包含了综合与探究,,与y轴交于点C,顶点为点D等内容,欢迎下载使用。
中考数学一轮复习考点复习专题18 函数与线段、面积等最值问题【考点精讲】(含解析): 这是一份中考数学一轮复习考点复习专题18 函数与线段、面积等最值问题【考点精讲】(含解析),共44页。试卷主要包含了二次函数与线段的和差,二次函数与周长,二次函数与距离,二次函数与面积,三点等内容,欢迎下载使用。