高中数学人教B版 (2019)必修 第二册5.4 统计与概率的应用多媒体教学课件ppt

这是一份高中数学人教B版 (2019)必修 第二册5.4 统计与概率的应用多媒体教学课件ppt，共23页。PPT课件主要包含了方法二，显然AEF，课堂小结等内容，欢迎下载使用。

抽样方法:简单随机抽样、分层抽样;数据的数字特征:最值、平均数、方差、中位数、百分位数、众数、极差等;数据的直观表示:频率分布表、频率分布直方图、茎叶图等;用样本估计总体:用样本的数据特征估计总体的数据体征、用样本的分布估计总体分布.
样本空间、事件、事件之间的运算以及对应的概率之间的关系;确定事件概率的方法:古典概型、频率估计概率;事件的独立性以及有关的概率计算.
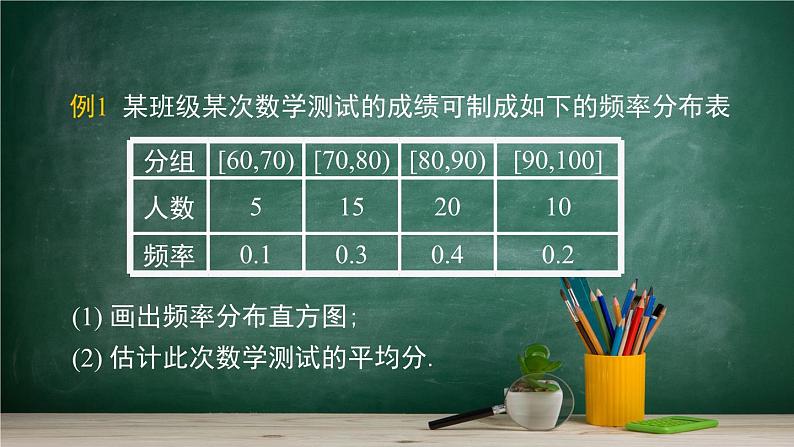
例1 某班级某次数学测试的成绩可制成如下的频率分布表
(1) 画出频率分布直方图;(2) 估计此次数学测试的平均分.
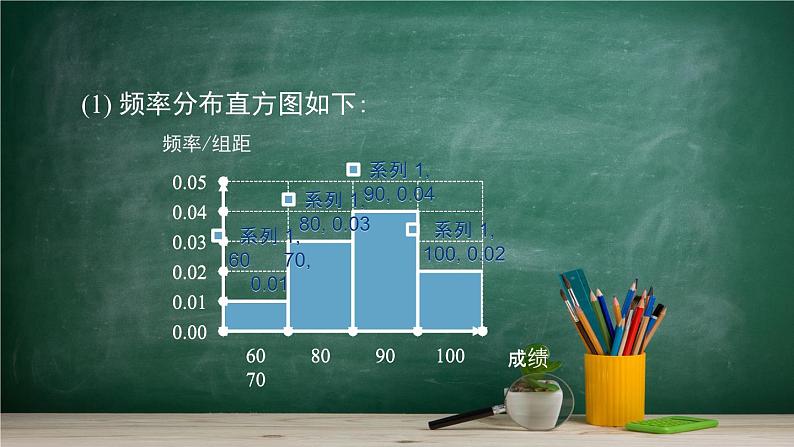
(1) 频率分布直方图如下:
我们无法通过频率分布表看出原始数据具体是多少,只知道有5个人的成绩大于等于60分,低于70分.将这五个人的成绩都用65分代替.
(2)
例2 人的卷舌与平舌（指是否能左右卷起来）同人的眼皮的单双一样,也是由遗传自父母的基因决定的,其中显性基因记为D,隐形基因记为d ;成对的基因中,只要出现了显性基因,就一定是卷舌的(这就是说,“卷舌”的充要条件是:“基因对是 ”).同前面一样,决定眼皮单双的基因仍记为B（显性基因）和b（隐性基因）.
有一对夫妻,两人决定舌头形态和眼皮单双的基因都是DdBb,不考虑基因突变,求他们的孩子是卷舌且单眼皮的概率.
有关生物学知识表明:控制上述两种不同性状的基因遗传时互不干扰.
解:方法一这对夫妻孩子的决定舌头形态和眼皮单双的基因的所有可能如下:
不难看出,样本空间共包含16个样本点,每组基因对发生的可能性相等.记A:他们的孩子是卷舌且单眼皮
所以 .
记E:他们的孩子是卷舌记F:他们的孩子是单眼皮记A:他们的孩子是卷舌且单眼皮
先考虑孩子舌头形态,由右图可知 ;同理, .
由题意事件E与事件F相互独立,所以, .
利用古典概型确定随机事件的概率时,应该满足基本事件的有限性和发生的等可能性.当样本空间中的样本点个数比较多时,可以借助树状图等图表,直观地展示所有的样本点.当直接计算随机事件的概率比较复杂时,我们也可以理清各个随机事件之间的关系,借助相应的概率运算公式进行运算.
例3 人们在接受问卷调查时,通常不愿意如实回答太敏感的问题.例如,对于问题“捡到东西后是否有据为己有的行为”,有些人会有说了实话会被人看不起的顾虑;再比如,直接问运动员们是否服用过兴奋剂,绝大多数情况下也难以得到真实的数据.怎样才能让人们打消顾虑如实回答敏感的问题呢?你能想出好办法吗?
解决这个问题的关键之处在于:既要让被调查者根据自己的实际情况做出“是”或“否”的回答.又能保护被调查者的隐私,让他们清楚,不管他回答“是”还是“否”,别人都不知道他是否有“捡到东西据为己有的行为”.问卷上再设置一个非敏感性问题,被调查者回答其中一个问题即可.调查者无权过问被调查者回答的是哪一个问题.
非敏感性问题有很多,选择怎样的非敏感性问题呢？我们进行问卷调查的目的是为了估计“捡到东西后据为己有”这种行为发生的概率有多大.所以,我们需要知道如果被调查者回答的是我们设置的非敏感性问题,他回答“是”的概率是多大.选择知道回答“是”的概率的非敏感性问题.
当我们选定了一个非敏感性问题,例如:问题一:您的身份证号码最后一个数是奇数吗?问题二:捡到东西后是否有据为己有的行为?○是 ○否被调查者如果回答的是问题一,那么他有一半的可能性选择“是”.
我们需要知道收回的问卷上的答案是针对问题一做出的回答还是针对问题二做出的回答？我们无权过问被调查者回答的是哪个问题,如何知道有多少人回答了问题一,多少人回答了问题二,设置一个随机化的装置,例如抛一枚质地均匀的硬币,如果得到正面,回答问题一;如果得到反面,回答问题二.
问卷:在回答前,请背对被调查者自行抛一个硬币:如果得到正面,请按照问题一勾选答案;如果得到反面,请按照问题二勾选答案.问题一:您的身份证号码最后一个数是奇数吗?问题二:捡到东西后是否有据为己有的行为?○是 ○否
统计推断如果收回的200份问卷里,有62份答“是”,试估计“捡到东西后据为己有”这种行为的概率？
解:回答问题一的人数为100,其中回答“是”的人数可估计为50;回答问题二的人数为100,其中回答“是”的人数为: ;所以该行为发生的概率可估计为12%.
问题分析与符号说明概率模型的建立概率的求解问题的解决
数据收集数据整理数据分析统计推断