第二十四章 圆 单元过关检测02-2022-2023学年九年级数学上册同步考点知识清单＋例题讲解＋课后练习（人教版）

这是一份第二十四章 圆 单元过关检测02-2022-2023学年九年级数学上册同步考点知识清单＋例题讲解＋课后练习（人教版），文件包含九年级数学上册第二十四章圆单元过关检测02原卷版docx、九年级数学上册第二十四章圆单元过关检测02解析版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

2022—2023学年九年级上学期第四单元（2）
一、选择题（本题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔把答题卡上对应题目答案标号涂黑）
1．（4分）已知⊙O的半径是3cm，则⊙O中最长的弦长是（　　）
A．3cm B．6cm C．1.5cm D．cm
【分析】利用圆的直径为圆中最长的弦求解．
【解答】解：∵圆的直径为圆中最长的弦，
∴⊙O中最长的弦长为2×3＝6（cm）．
故选：B．
2．（4分）如图，一个圆柱形的玻璃水杯，将其横放，截面是个半径为5cm的圆，杯内水面宽AB＝8cm，则水深CD是（　　）

A．3cm B．2cm C． D．
【分析】连接OA、OC，先由垂径定理可得AC长，再由勾股定理得OD长，从而求出CD长．
【解答】解：如图，连接OA、OC，
则OC⊥AB，
∴AC＝AB＝4（cm），
在Rt△OAD中，OD＝＝＝3（cm），
∴CD＝5﹣3＝2（cm）．
故选：B．

3．（4分）如图，AB是半圆O的直径，以弦AC为折痕折叠后，恰好经过点O，则∠AOC等于（　　）

A．120° B．125° C．130° D．145°
【分析】根据翻折变换得出AC垂直平分OQ，AQ＝AO，求出△AQO是等边三角形，求出∠AOQ＝60°，再根据等腰三角形的性质得出∠COQ＝∠AOQ，再求出答案即可．
【解答】解：O关于直线AC的对称点是Q，连接OQ，交AC于M，

则AC垂直平分OQ，
即AQ＝AO，OM⊥AC，
∵OQ＝OA，
∴OQ＝AQ＝OA，
∴△AQO是等边三角形，
∴∠AOQ＝60°，
∵OQ⊥AC，OA＝OC，
∴∠COQ＝∠AOQ＝60°，
∴∠AOC＝60°+60°＝120°，
故选：A．
4．（4分）如图，在Rt△ACB中∠ACB＝60°，以直角边AB为直径的⊙O交线段AC于点E，点M是弧AE的中点，OM交AC于点D，⊙O的半径是6，则MD的长度为（　　）

A． B． C．3 D．
【分析】根据三角形内角和定理求出∠A＝30°，根据垂径定理求出OD⊥AE，根据含30°角的直角三角形的性质求出OD，再求出MD即可．
【解答】解：∵∠ABC＝90°，∠ACB＝60°，
∴∠A＝30°，
∵M为弧AE的中点，OM过圆心O，
∴OM⊥AD，
∴∠ADO＝90°，
∴OD＝OA＝＝3，
∴MD＝OM﹣OD＝6﹣3＝3，
故选：C．
5．（4分）如图，AD是⊙O的直径，PA，PB分别切⊙O于点A，B，若∠BCD＝α，则∠P的度数是（　　）

A．90°﹣2α B．90°﹣α C．45° D．2α
【分析】连接OB，利用圆周角定理可得∠BOD＝2α，然后利用切线的性质可得∠OAP＝∠OBP＝90°，从而利用四边形内角和可得∠P+∠AOB＝180°，最后利用同角的补角相等即可解答．
【解答】解：连接OB，

∵∠BCD＝α，
∴∠BOD＝2∠BCD＝2α，
∵PA，PB分别切⊙O于点A，B，
∴∠OAP＝∠OBP＝90°，
∴∠P+∠AOB＝360°﹣∠OAP﹣∠OBP＝180°，
∵∠AOB+∠BOD＝180°，
∴∠P＝∠BOC＝2α，
故选：D．
6．（4分）如图，要用一个扇形纸片围成一个无底盖的圆锥（接缝处忽略不计），若该圆锥的底面圆周长为20πcm，侧面积为240πcm2，则这个扇形的圆心角的度数是（　　）度．

A．120° B．135° C．150° D．160°
【分析】先设圆锥的母线长为lcm，由于圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长，则根据扇形的面积公式得到×20π×l＝240π，解得l＝24，然后设这个扇形的圆心角的度数是n°，利用弧长公式得到20π＝，最后解方程即可．
【解答】解：设圆锥的母线长为lcm，
则×20π×l＝240π，
解得l＝24，
设这个扇形的圆心角的度数是n°，
根据题意得20π＝，
解得n＝150，
即这个扇形的圆心角的度数是150°．
故选：C．
7．（4分）工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图（1）所示的工件槽，其两个底角均为90°，将形状规则的铁球放入槽内时，若同时具有图（1）所示的A、B、E三个接触点，该球的大小就符合要求．图（2）是过球心及A、B、E三点的截面示意图，已知⊙O的直径就是铁球的直径，AB是⊙O的弦，CD切⊙O于点E，AC⊥CD、BD⊥CD，若CD＝16cm，AC＝BD＝4cm，则这种铁球的直径为（　　）

A．10cm B．15cm C．20cm D．24cm
【分析】连接OE，交AB于点F，连接OA，∵AC⊥CD、BD⊥CD，由矩形的判断方法得出四边形ACDB是矩形，得出AB∥CD，AB＝CD＝16cm，由切线的性质得出OE⊥CD，得出OE⊥AB，得出四边形EFBD是矩形，AF＝AB＝×16＝8（cm），进而得出EF＝BD＝4cm，设⊙O的半径为rcm，则OA＝rcm，OF＝OE﹣EF＝（r﹣4）cm，由勾股定理得出方程r2＝82+（r﹣4）2，解方程即可求出半径，继而求出这种铁球的直径．
【解答】解：如图，连接OE，交AB于点F，连接OA，

∵AC⊥CD、BD⊥CD，
∴AC∥BD，
∵AC＝BD＝4cm，
∴四边形ACDB是平行四边形，
∴四边形ACDB是矩形，
∴AB∥CD，AB＝CD＝16cm，
∵CD切⊙O于点E，
∴OE⊥CD，
∴OE⊥AB，
∴四边形EFBD是矩形，AF＝AB＝×16＝8（cm），
∴EF＝BD＝4cm，
设⊙O的半径为rcm，则OA＝rcm，OF＝OE﹣EF＝（r﹣4）cm，
在Rt△AOF中，OA2＝AF2+OF2，
∴r2＝82+（r﹣4）2，
解得：r＝10，
∴这种铁球的直径为20cm，
故选：C．
8．（4分）如图，两张完全相同的正六边形纸片（边长为2a）重合在一起，下面一张保持不动，将上面一张纸片六边形A'B'C'D'E'F'沿水平方向向左平移a个单位长度，则上面正六边形纸片面积与折线A'﹣B'﹣C扫过的面积（阴影部分面积）之比是（　　）

A．3：1 B．4：1 C．5：2 D．2：1
【分析】求出正六边形和阴影部分的面积即可解决问题．
【解答】解：正六边形的面积＝6××（2a）2＝6a2，
阴影部分的面积＝a•2a＝2a2，
∴空白部分与阴影部分面积之比是＝6a2：2a2＝3：1，
故选：A．
9．（4分）如图，将两个正方形如图放置（B，C，E共线，D，C，G共线），若AB＝3，EF＝2，点O在线段BC上，以OF为半径作⊙O，点A，点F都在⊙O上，则OD的长是（　　）

A．4 B． C． D．
【分析】设OC＝x，根据圆上的点到圆心的距离相等，得＝，进而求得x＝1，再根据勾股定理解决此题．
【解答】解：设OC＝x．
由题意得，OA＝OF．
∴＝．
∴．
∴x＝1．
∴OD＝＝．
故选：B．


10．（4分）某餐厅为了追求时间效率，推出一种液体“沙漏”免单方案（即点单完成后，开始倒转“沙漏”，“沙漏”漏完前，客人所点的菜需全部上桌，否则该桌免费用餐）．“沙漏”是由一个圆锥体和一个圆柱体相通连接而成．某次计时前如图（1）所示，已知圆锥体底面半径是6cm，高是6cm；圆柱体底面半径是3cm，液体高是7cm．计时结束后如图（2）所示，求此时“沙漏”中液体的高度为（　　）

A．2cm B．3cm C．4cm D．5cm
【分析】由圆锥体底面半径是6cm，高是6cm，可得CD＝DE，根据圆锥、圆柱体积公式可得液体的体积为63πcm3，圆锥的体积为72πcm3，即知计时结束后，圆锥中没有液体的部分体积为9πcm3，设计时结束后，“沙漏”中液体的高度AD为xcm，可得π•（6﹣x）2•（6﹣x）＝9π，即可解得答案．
【解答】解：如图：

∵圆锥的圆锥体底面半径是6cm，高是6cm，
∴△ABC是等腰直角三角形，
∴△CDE也是等腰直角三角形，即CD＝DE，
由已知可得：液体的体积为π×32×7＝63π（cm3），圆锥的体积为π×62×6＝72π（cm3），
∴计时结束后，圆锥中没有液体的部分体积为72π﹣63π＝9π（cm3），
设计时结束后，“沙漏”中液体的高度AD为xcm，则CD＝DE＝（6﹣x）cm，
∴π•（6﹣x）2•（6﹣x）＝9π，
∴（6﹣x）3＝27，
解得x＝3，
∴计时结束后，“沙漏”中液体的高度为3cm，
故选：B．
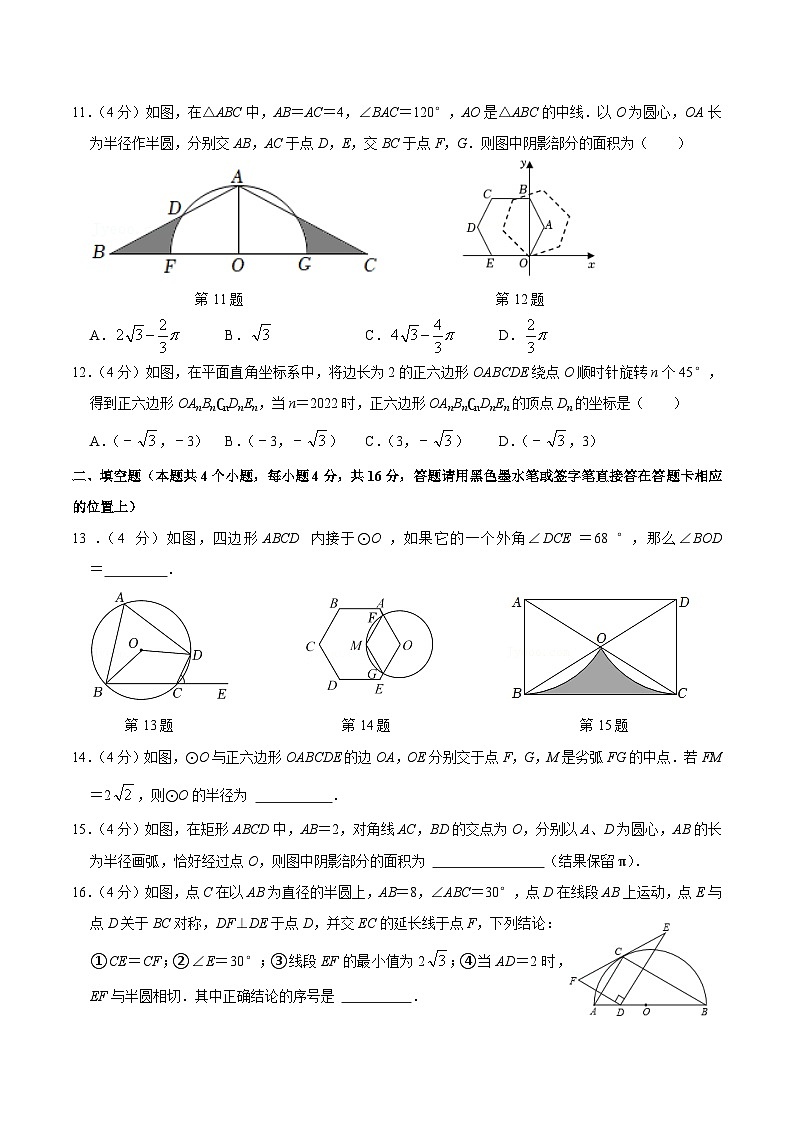
11．（4分）如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，AO是△ABC的中线．以O为圆心，OA长为半径作半圆，分别交AB，AC于点D，E，交BC于点F，G．则图中阴影部分的面积为（　　）

A． B． C． D．
【分析】连接DO，过点O作OH⊥AB，垂足为H，如图，由已知条件根据等腰三角形的性质可得∠ABO的度数，根据含30°角的直角三角形的性质可得，AO的长度，根据勾股定理可得BO的长度，即可算出S△ABO＝的面积，由∠BAOO＝60°，可得∠AOH＝30°，即可算出HO，AH的长，即可算出S△ADO＝的面积，根据扇形面积的计算方法可得S扇DOF＝的面积，根据面积差可得S阴BDF＝S△ABO﹣S△ADO﹣S扇DOF的面积，由S阴＝2S阴BDF即可得出答案．
【解答】解：连接DO，过点O作OH⊥AB，垂足为H，如图，
∵AB＝AC＝4，∠BAC＝120°，
∴＝30°，
∴＝2，BO＝＝＝2，
∴S△ABO＝＝2＝2，
∵∠ABO＝60°，
∴∠AOH＝30°，
∴＝＝1，AH＝＝＝，
∴S△ADO＝＝＝，
∵∠DOF＝90°﹣60°＝30°，DO＝2，
S扇DOF＝＝＝，
S阴BDF＝S△ABO﹣S△ADO﹣S扇DOF＝2﹣＝，
S阴＝2S阴BDF＝2．
故选：A．

12．（4分）如图，在平面直角坐标系中，将边长为2的正六边形OABCDE绕点O顺时针旋转n个45°，得到正六边形OAnBn∁nDnEn，当n＝2022时，正六边形OAnBn∁nDnEn的顶点Dn的坐标是（　　）

A．（﹣，﹣3） B．（﹣3，﹣） C．（3，﹣） D．（﹣，3）
【分析】由题意旋转8次应该循环，因为2022÷8＝252…6，所以Dn的坐标与D6的坐标相同．
【解答】解：由题意旋转8次应该循环，
∵2022÷8＝252…6，
∴Dn的坐标与D6的坐标相同，
如图，过点D6H⊥OE于点H，

∵∠DOD6＝90°，∠DOE＝30°，OD＝OD6＝2，
∴OH＝OD6•cos60°＝，HD6＝OH＝3，
∴D6（﹣，﹣3），
∴顶点Dn的坐标是（﹣，﹣3），
故选：A．
二、填空题（本题共4个小题，每小题4分，共16分，答题请用黑色墨水笔或签字笔直接答在答题卡相应的位置上）
13．（4分）如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE＝68°，那么∠BOD＝　 　．

【分析】先根据圆内接四边形的性质和邻补角的定义得到∠A+∠BCD＝180°，∠DCE+∠BCD＝180°，则∠A＝∠DCE＝68°，然后根据圆周角定理求解即可．
【解答】解：∵∠A+∠BCD＝180°，∠DCE+∠BCD＝180°，
∴∠A＝∠DCE＝68°，
∴∠BOD＝2∠A＝136°．
故答案为：136°．
14．（4分）如图，⊙O与正六边形OABCDE的边OA，OE分别交于点F，G，M是劣弧FG的中点．若FM＝2，则⊙O的半径为 　 　．

【分析】根据正六边形的性质以及圆周角定理可得出四边形OFMG是菱形，进而得到半径．
【解答】解：如图，连接OM，
∵六边形OABCDE是正六边形，
∴∠AOE＝＝120°，
∵M是劣弧FG的中点．
∴∠AOM＝∠EOM＝∠AOB＝60°，
又∵OF＝OG＝OM，
∴四边形OEMG是菱形，
∴OE＝MF＝2，
即⊙O的半径为2，
故答案为：2．

15．（4分）如图，在矩形ABCD中，AB＝2，对角线AC，BD的交点为O，分别以A、D为圆心，AB的长为半径画弧，恰好经过点O，则图中阴影部分的面积为 　 　（结果保留π）．

【分析】根据已知得△AOB，△COD都为边长为2的等边三角形，BC＝2，所以阴影部分的面积为三角形OBC的面积减去两个弓形的面积．
【解答】解：根据已知得△AOB，△COD都为边长为2的等边三角形，
∴BC＝2，
∵△AOB，△COD的面积为2×＝，扇形BAO和扇形CDO的面积为＝，
∴阴影部分的面积为2×﹣2×（﹣）＝3﹣π．
故答案为：3﹣π．
16．（4分）如图，点C在以AB为直径的半圆上，AB＝8，∠ABC＝30°，点D在线段AB上运动，点E与点D关于BC对称，DF⊥DE于点D，并交EC的延长线于点F，下列结论：
①CE＝CF；②∠E＝30°；③线段EF的最小值为2；④当AD＝2时，EF与半圆相切．其中正确结论的序号是 　 　．

【分析】①由点E与点D关于AC对称可得CE＝CD，再根据DF⊥DE即可证到CE＝CF，从而判断正误；
②由对称性质得BC⊥DE，∠BCD＝∠BCE，当∠BCD≠60°时，∠E≠30°，从而判断正误；
③根据“点到直线之间，垂线段最短”可得CD⊥AB时CD最小，由于EF＝2CD，求出CD的最小值就可求出EF的最小值，从而判断正误；
④连接OC，易证△AOC是等边三角形，AD＝OD，根据等腰三角形的“三线合一”可求出∠ACD，进而可求出∠ECO＝90°，从而得到EF与半圆相切，从而判断正误．
【解答】解：①连接CD，

∵点E与点D关于AC对称，
∴CE＝CD．
∴∠E＝∠CDE．
∵DF⊥DE，
∴∠EDF＝90°．
∴∠E+∠F＝90°，∠CDE+∠CDF＝90°．
∴∠F＝∠CDF．
∴CD＝CF．
∴CE＝CD＝CF．
故①的结论正确；
②∵点E与点D关于AC对称，
∴DE⊥BC，∠BCD＝∠BCE，
当∠BCD≠60°时，∠E≠30°，
故②的结论错误；
③当CD⊥AB时，
∵AB是半圆的直径，
∴∠ACB＝90°．
∵AB＝8，∠CBA＝30°，
∴∠CAB＝60°，AC＝4，BC＝4．
∵CD⊥AB，∠CBA＝30°，
∴CD＝BC＝2．
根据“点到直线之间，垂线段最短”可得点D在线段AB上运动时，CD的最小值为2．
∵CE＝CD＝CF，
∴EF＝2CD．
∴线段EF的最小值为4．
故③的结论错误；
③当AD＝2时，连接OC，

∵OA＝OC，∠CAB＝60°，
∴△OAC是等边三角形．
∴CA＝CO，∠ACO＝60°．
∵AO＝4，AD＝2，
∴DO＝2．
∴AD＝DO．
∴∠ACD＝∠OCD＝30°，
∴∠BCO＝30°，
∵点E与点D关于AC对称，
∴∠ECB＝∠DCB＝60°．
∴∠ECO＝90°．
∴OC⊥EF．
∵EF经过半径OC的外端，且OC⊥EF，
∴EF与半圆相切．
故④的结论正确；
故答案为：①④．
三、解答题（本题共8个小题，共86分，答题请用黑色墨水笔或签字笔直接答在答题卡相应的位置上，解答时应写出必要的文字说明、证明步骤或演算步骤.）
17．（8分）如图，AB为⊙O的直径，E为OB的中点，弦CD⊥AB于点E，连接CO并延长交⊙O于点F，连接BC．
（1）求证：△BOC是等边三角形；
（2）若⊙O的半径为2，求CD的长．

【分析】（1）根据等边三角形的判定定理证明即可；
（2）根据勾股定理和垂径定理解答即可．
【解答】（1）证明：∵E为OB的中点，
∴OE＝OB＝OC，
∵弦CD⊥AB于点E，
∴∠COE＝30°，
∴∠COE＝60°，
又∵OC＝OB，
∴△BOC是等边三角形；
（2）解：在Rt△COE中，CO＝2，OE＝1，
∴CE＝，
∵AB是⊙O的直径，弦CD⊥AB于点E，
∴CE＝DE＝CD，
∴CD＝2CE＝2．
18．（8分）石拱桥是我国古代入民勤劳和智慧的结晶（如图1），隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表．如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为．桥的跨度（弧所对的弦长）AB＝26m，设所在圆的圆心为O，半径OC⊥AB，垂足为D．拱高（弧的中点到弦的距离）CD＝5m．连接OB．
（1）直接判断AD与BD的数量关系；
（2）求这座石拱桥主桥拱的半径（精确到1m）．

【分析】（1）根据垂径定理便可得出结论；
（2）设主桥拱半径为R，在Rt△OBD中，根据勾股定理列出R的方程便可求得结果．
【解答】解：（1）∵OC⊥AB，
∴AD＝BD；
（2）设主桥拱半径为R，由题意可知AB＝26，CD＝5，
∴BD＝AB＝13，
OD＝OC﹣CD＝R﹣5，
∵∠ODB＝90°，
∴OD2+BD2＝OB2，
∴（R﹣5）2+132＝R2，
解得R＝19.4≈19，
答：这座石拱桥主桥拱的半径约为19m．
19．（10分）如图，四边形ABCD是⊙O的内接四边形，点F是CD延长线上的一点，且AD平分∠BDF，AE⊥CD于点E．
（1）求证：AB＝AC．
（2）若BD＝18，DE＝2，求CD的长．

【分析】（1）根据角平分线的定义、圆内接四边形的性质解答；
（2）过点A作AG⊥BD，分别证明Rt△AED≌Rt△AGD和Rt△AEC≌Rt△AGB，根据全等三角形的性质计算．
【解答】（1）证明：∵AD平分∠BDF，
∴∠ADF＝∠ADB，
∵∠ABC+∠ADC＝180°，∠ADC+∠ADF＝180°，
∴∠ADF＝∠ABC，
∵∠ACB＝∠ADB，
∴∠ABC＝∠ACB，
∴AB＝AC；
（2）解：过点A作AG⊥BD，垂足为点G．
∵AD平分∠BDF，AE⊥CF，AG⊥BD，
∴AG＝AE，∠AGB＝∠AEC＝90°，
在Rt△AED和Rt△AGD中，
，
∴Rt△AED≌Rt△AGD，
∴GD＝ED＝2，
在Rt△AEC和Rt△AGB中，
，
∴Rt△AEC≌Rt△AGB（HL），
∴BG＝CE，
∵BD＝18，
∴BG＝BD﹣GD＝18﹣2＝16，
∴CE＝BG＝16，
∴CD＝CE﹣DE＝16﹣2＝14．

20．（10分）如图，AB是⊙O的直径，点C为的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．
（1）求证：△BFG≌△CDG；
（2）若AD＝BE＝4，求BF的长．

【分析】（1）首先利用已知条件和垂径定理证明CD＝BF，然后根据AAS证明△BFG≌△CDG；
（2）连接OF，设⊙O的半径为r，由CF＝BD列出关于r的勾股方程就能求解．
【解答】（1）证明：∵C是 中点，
∴＝，
∵AB是⊙O的直径，且CF⊥AB，
∴＝，
∴＝，
∴CD＝BF，
在△BFG和△CDG中，
，
∴△BFG≌△CDG（AAS）；
（2）解：如图，连接OF，设⊙O的半径为r，
Rt△ADB中，BD2＝AB2﹣AD2，即BD2＝（2r）2﹣42，
Rt△OEF中，OF2＝OE2+EF2，即EF2＝r2﹣（r﹣4）2，
∵＝＝，
∴＝，
∴BD＝CF，
∴BD2＝CF2＝（2EF）2＝4EF2，
即（2r）2﹣42＝4[r2﹣（r﹣4）2]，
解得：r＝2（舍）或6，
∴BF2＝EF2+BE2＝62﹣（6﹣4）2+42＝48，
∴BF＝4．

21．（12分）如图，等边三角形ABC内接于半径长为2的⊙O，点P在圆弧AB上以2倍速度从B向A运动，点Q在圆弧BC上以1倍速度从C向B运动，当点P，O，Q三点处于同一条直线时，停止运动．
（1）求点Q的运动总长度；
（2）若M为弦PB的中点，求运动过程中CM的最大值．

【分析】（1）因为点P在圆弧AB上以2倍速度从B向A运动，点Q在圆弧BC上以1倍速度从C向B运动，所以可以假设∠COQ＝n，∠BOP＝2n，可得120°﹣n+2n＝180°，求出n，可得结论；
（2）如图，取OB的中点J，连接JM，JC，过点J作JH⊥BC于点H．分别求出CJ，JM，可得结论．
【解答】解：（1）∵点P在圆弧AB上以2倍速度从B向A运动，点Q在圆弧BC上以1倍速度从C向B运动，
∴可以假设∠COQ＝n，∠BOP＝2n，
∵△ABC是等边三角形，
∴∠A＝60°，
∴∠BCO＝2∠A＝120°，
∵P，O，Q共线，
∴120°﹣n+2n＝180°，
∴n＝60°，
∴点Q的运动总长度＝＝；
（2）如图，取OB的中点J，连接JM，JC，过点J作JH⊥BC于点H．

∵OB＝OC＝2，∠BOC＝120°，
∴BC＝OB＝2，∠OBC＝∠OCB＝30°，
∵BJ＝OJ＝1，
∴JH＝BJ＝，BH＝，
∴CH＝，
∴CJ＝＝＝，
∵BM＝MP．BJ＝OJ，
∴JM＝OP＝1，
∴CM≤JM+CJ＝1+，
∴CM的最大值为1+．
22．（12分）如图，C是圆O被直径AB分成的半圆上一点，过点C的圆O的切线交AB的延长线于点P，连接CA，CO，CB．
（1）求证：∠ACO＝∠BCP；
（2）若∠ABC＝2∠BCP，求∠P的度数；
（3）在（2）的条件下，若AB＝4，求图中阴影部分的面积（结果保留π和根号）．

【分析】（1）由AB是半圆O的直径，CP是半圆O的切线，可得∠ACB＝∠OCP，即得∠ACO＝∠BCP；
（2）由∠ABC＝2∠BCP，可得∠ABC＝2∠A，从而∠A＝30°，∠ABC＝60°，可得∠P的度数是30°；
（3）∠A＝30°，可得BC＝AB＝2，AC＝BC＝2，即得S△ABC＝BC•AC＝2，故阴影部分的面积是π×（）2﹣2＝2π﹣2．
【解答】（1）证明：∵AB是半圆O的直径，
∴∠ACB＝90°，
∵CP是半圆O的切线，
∴∠OCP＝90°，
∴∠ACB＝∠OCP，
∴∠ACO＝∠BCP；
（2）解：由（1）知∠ACO＝∠BCP，
∵∠ABC＝2∠BCP，
∴∠ABC＝2∠ACO，
∵OA＝OC，
∴∠ACO＝∠A，
∴∠ABC＝2∠A，
∵∠ABC+∠A＝90°，
∴∠A＝30°，∠ABC＝60°，
∴∠ACO＝∠BCP＝30°，
∴∠P＝∠ABC﹣∠BCP＝60°﹣30°＝30°，
答：∠P的度数是30°；
（3）解：由（2）知∠A＝30°，
∵∠ACB＝90°，
∴BC＝AB＝2，AC＝BC＝2，
∴S△ABC＝BC•AC＝×2×2＝2，
∴阴影部分的面积是π×（）2﹣2＝2π﹣2，
答：阴影部分的面积是2π﹣2．
23．（12分）如图，以线段AB为直径作⊙O，交射线AC于点C，AD平分∠CAB交⊙O于点D，过点D作直线DE⊥AC于点E，交AB的延长线于点F．连接BD并延长交AC于点M．
（1）求证：直线DE是⊙O的切线；
（2）若∠F＝30°，求∠M的度数；
（3）在第二问的条件下，若ME＝1，求BF的长．

【分析】（1）连接OD，由∠ODA＝∠OAD＝∠DAC证明OD∥AC，得∠ODF＝∠AED＝90°，即可证明直线DE是⊙O的切线；
（2）根据圆周角定理和等边三角形的判定和性质即可得到结论；
（3）由∠AEF＝90°，∠F＝30°证明∠BAM＝60°，则△ABM是等边三角形，所以∠M＝60°，则∠EDM＝30°，所以BD＝MD＝2ME＝2，再证明∠BDF＝∠F，得BF＝BD＝2．
【解答】（1）证明：连接OD，则OD＝OA，
∴∠ODA＝∠OAD，
∵AD平分∠CAB，
∴∠OAD＝∠DAC，
∴∠ODA＝∠DAC，
∴OD∥AC，
∵DE⊥AC，
∴∠ODF＝∠AED＝90°，
∵OD是⊙O的半径，且DE⊥OD，
∴直线DE是⊙O的切线；
（2）解：∵线段AB是⊙O的直径，
∴∠ADB＝90°，
∴∠ADM＝180°﹣∠ADB＝90°，
∴∠M+∠DAM＝90°，∠ABM+∠DAB＝90°，
∵∠DAM＝∠DAB，
∴∠M＝∠ABM，
∴AB＝AM．
∵∠AEF＝90°，∠F＝30°，
∴∠BAM＝60°，
∴△ABM是等边三角形，
∴∠M＝60°；
（3）解：∵∠DEM＝90°，∠M＝60°，ME＝1，
∴∠EDM＝30°，
∴MD＝2ME＝2，
∴BD＝MD＝2，
∵∠BDF＝∠EDM＝30°，
∴∠BDF＝∠F，
∴BF＝BD＝2．

24．（14分）如图，在△ABC中，D在边AC上，圆O为锐角△BCD的外接圆，连结CO并延长交AB于点E．
（1）若∠DBC＝α，请用含α的代数式表示∠DCE；
（2）如图2，作BF⊥AC，垂足为F，BF与CE交于点G，已知∠ABD＝∠CBF．
①求证：EB＝EG；
②若CE＝5，AC＝8，求FG+FB的值．

【分析】（1）根据圆周角定理即可解决问题；
（2）①结合（1）利用三角形内角和定理即可解决问题；
②作EM⊥BE，EN⊥AC，证明四边形EMFN为矩形，再根据线段的和差即可解决问题．
【解答】（1）解：如图，连结OD，

∵∠DOC＝2∠DBC＝2α，
又∵OD＝OC，
∴∠DCE＝90°﹣α；
（2）①证明：∵∠ABD＝∠CBF，
∴∠EBG＝∠ABD+∠DBF＝∠CBF+∠DBF＝∠DBC，
设∠DBC＝α，
由（1）得：∠DCE＝90°﹣α，
∵BF⊥AC，
∴∠FGC＝∠BGE＝α，
∴∠EBG＝∠EGB，
∴EB＝EG；
②解：如图，作EM⊥BE，EN⊥AC，

由①得：∠EBG＝α，∠ACE＝90°﹣α，
∵BF⊥AC
∴∠A＝90°﹣α，
∴AE＝CE＝5，
∵EN⊥AC，AC＝8，
∴CN＝4，
∴EN＝3，
∵EM⊥BF，NF⊥BF，EN⊥AC，
∴四边形EMFN为矩形，
∴EN＝MF＝3，
∵EB＝EG，EM⊥BG，
∴BM＝GM，
∴FG+FB＝FM﹣MG+FM+BM＝2FM＝6．