2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第七节函数的图象课件

这是一份2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第七节函数的图象课件，共43页。PPT课件主要包含了必备知识·夯实双基，关键能力·题型突破，fx－a，fx＋b，2伸缩变换，fωx，Afx，－fx，f－x，－f－x等内容，欢迎下载使用。

【课标标准】　1.掌握基本初等函数的图象特征，能熟练运用基本初等函数的图象解决问题.2.掌握图象的作法：描点法和图象变换.3.会运用函数图象研究函数的性质．
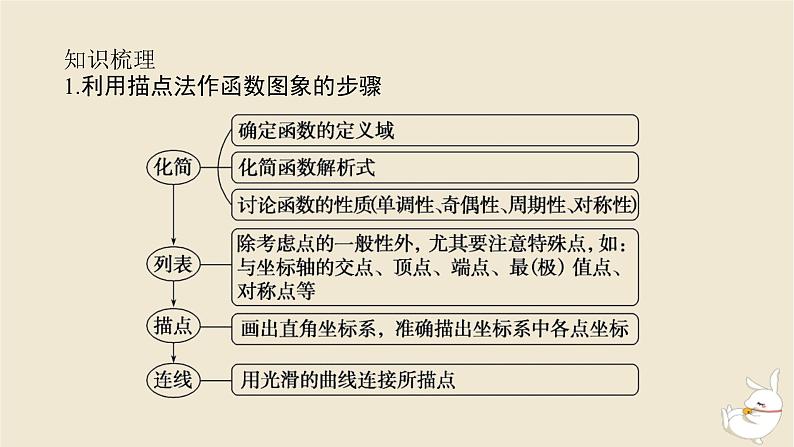
知识梳理1.利用描点法作函数图象的步骤
2．利用图象变换法作函数的图象(1)平移变换：
[常用结论]1．记住几个重要结论(1)函数y＝f(x)与y＝f(2a－x)的图象关于直线x＝a对称．(2)函数y＝f(x)与y＝2b－f(2a－x)的图象关于点(a，b)中心对称．(3)若函数y＝f(x)对定义域内任意自变量x满足：f(a＋x)＝f(a－x)，则函数y＝f(x)的图象关于直线x＝a对称．2．图象的左右平移仅仅是相对于x而言，如果x的系数不是1，常需把系数提出来，再进行变换．3．图象的上下平移仅仅是相对于y而言的，利用“上加下减”进行．
夯实双基1.思考辨析(正确的打“√”，错误的打“×”)(1)函数y＝f(1－x)的图象，可由y＝f(－x)的图象向左平移1个单位得到．(　　)(2)函数y＝f(x)的图象关于y轴对称即函数y＝f(x)与y＝f(－x)的图象关于y轴对称．(　　)(3)当x∈(0，＋∞)时，函数y＝f(|x|)的图象与y＝|f(x)|的图象相同．(　　)(4)若函数y＝f(x)满足f(1＋x)＝f(1－x)，则函数f(x)的图象关于直线x＝1对称．(　　)
解析：其图象是由y＝x2图象中x<0的部分和y＝x－1图象中x≥0的部分组成．故选C.
3．(教材改编)小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶，则与以上事件吻合最好的图象是(　　)
解析：与学校的距离应逐渐减小，由于小明先是匀速运动，故前段是直线段，途中停留时距离不变，后段加速，后段比前段下降得快．故选C.
5．(易错)若关于x的方程|x|＝a－x只有一个解，则实数a的取值范围是________．
解析：在同一直角坐标系中，画出函数y＝|x|和函数y＝－x＋a的图象如图，可知当a>0时，两函数有且只有一个交点，即|x|＝a－x只有一个解．
(2)y＝|lg2(x＋1)|；
解析：作出y＝lg2x的图象，将此图象向左平移1个单位，得到y＝lg2(x＋1)的图象，再保留其y≥0部分，加上其y＜0的部分关于x轴的对称部分，即得y＝|lg2(x＋1)|的图象(图2)．
题后师说图象变换应掌握的两点(1)熟练掌握几种基本初等函数的图象．(2)由某个基本初等函数的图象平移、翻折、对称和伸缩变换时，一定注意变换顺序．
巩固训练1作出下列函数的图象：(1)y＝2x＋1－1；
解析：将y＝2x的图象向左平移1个单位，得到y＝2x＋1的图象，再将所得图象向下平移1个单位得到y＝2x＋1－1的图象，如图所示．
巩固训练1作出下列函数的图象：(2)y＝x2－|x|－2.
解析：(2)由图象，x→0，y→0；x→＋∞，y→＋∞.对于B，x→＋∞，y→0.所以不符合图象；对于C，x→0，x>0，y→－∞.所以不符合图象；对于D，x→＋∞，y→0.所以不符合图象，最后可以确定只有A符合题意，故选A.
题后师说辨识函数图象的四种策略
巩固训练2(1)函数y＝ln (ex＋e－x)的图象大致是(　　)
解析：(1)由x＝0时y＝ln 2，排除B，C；又ex＋e－x≥2，当且仅当x＝0时等号成立，故ln (ex＋e－x)≥ln 2，排除D.故选A.
题型三　函数图象的应用角度一 研究函数的性质例 3 已知函数f(x)＝x|x|－2x，则下列结论正确的是(　　)A．f(x)是偶函数，递增区间是(0，＋∞)B．f(x)是偶函数，递减区间是(－∞，1)C．f(x)是奇函数，递减区间是(－1，1)D．f(x)是奇函数，递增区间是(－∞，0)
题后师说利用图象研究函数性质问题的思路
角度二 解不等式例 4 已知函数y＝f(x)的图象是如图所示的折线ACB，且函数g(x)＝lg2(x＋1)，则不等式f(x)≥g(x)的解集是(　　)A．{x|－1＜x≤0} B．{x|－1≤x≤1}C．{x|－1＜x≤1} D．{x|－1＜x≤2}
解析：由已知f(x)的图象，在此坐标系作出y＝lg2(x＋1)的图象，如图满足不等式f(x)≥lg2(x＋1)的x范围是－1＜x≤1.所以不等式f(x)≥lg2(x＋1)的解集是{x|－1＜x≤1}．故选C.
题后师说当不等式问题不能用代数法求解，但其对应函数的图象可作出时，常将不等式问题转化为两函数图象的上、下关系问题，从而利用数形结合思想求解． 
巩固训练4已知函数f(x)＝3x＋1－4x－5，则不等式f(x)<0的解集是________. 
解析：因为函数f(x)＝3x＋1－4x－5，所以不等式f(x)<0即为3x＋1<4x＋5，在坐标系中作出y＝3x＋1，y＝4x＋5的图象，如图所示，y＝3x＋1，y＝4x＋5都经过点A(－1，1)，B(1，9)，f(x)<0即y＝3x＋1的图象在y＝4x＋5图象的下方，由图象知：不等式f(x)<0的解集是(－1，1)．
题后师说当方程与基本初等函数有关时，可以通过函数图象来研究方程的根，方程f(x)＝0的根就是函数f(x)图象与x轴交点的横坐标，方程f(x)＝g(x)的根就是函数f(x)与g(x)图象交点的横坐标．