贵州安龙县2022-2023学年七年级数学第二学期期末综合测试模拟试题含答案

贵州安龙县2022-2023学年七年级数学第二学期期末综合测试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．若与|x﹣y﹣3|互为相反数，则x+y的值为（　　）

A．3 B．9 C．12 D．27

2．在ABCD中，AB=3cm，BC=4cm，则ABCD的周长是(   )

A．5cm B．7cm C．12cm D．14cm

3．某学习小组7名同学在一学期里阅读课外书籍的册数分别是：14，12，13，12，17，18，16，则这组数据中位数是（     ）

A．12    B．13    C．14    D．17

4．下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差s2:

根据表中数据,要从中进选择一名成的绩责好又发挥稳定的运动员参加比赛，应该选择(   )

A．乙 B．甲 C．丙 D．丁

5．在平行四边形中，下列结论一定成立的是（     ）

A． B． C． D．

6．年一季度，华为某销公营收入比年同期增长，年第一季度营收入比年同期增长，年和年第一季度营收入的平均增长率为，则可列方程(   )

A． B．

C． D．

7．下列命题的逆命题不正确的是(     )

A．若，则 B．两直线平行，内错角相等

C．等腰三角形的两个底角相等 D．对顶角相等

8．下列二次根式中，化简后能与合并的是　　

A． B． C． D．

9．在平面直角坐标系内，已知点A的坐标为（-6，0），直线l：y=kx+b不经过第四象限，且与x轴的夹角为30°，点P为直线l上的一个动点，若点P到点A的最短距离是2，则b的值为（　　）

A． 或 B． C．2 D．2或10

10．化简正确的是（      ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．用配方法解一元二次方程x2-mx=1时，可将原方程配方成(x-3)2=n，则m+n的值是 ________ .

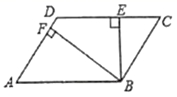
12．如图，在平行四边形ABCD中，，，垂足分别为E、F，，，，则平行四边形ABCD的面积为_________．

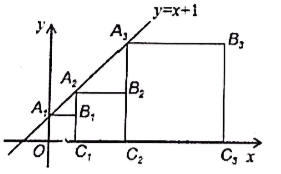
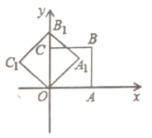
13．正方形，，，...按如图的方式放置，点，，...和点，，...分别在直线和轴上，则点的坐标为_______.

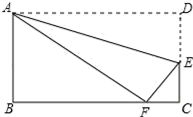
14．如图，沿折痕AE折叠矩形ABCD的一边，使点D落在BC边上一点F处．若AB=8，且△ABF的面积为24，则EC的长为__．

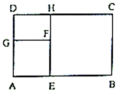
15．如图，在矩形中，不重叠地放上两张面积分别是和的正方形纸片和.矩形没被这两个正方形盖住的面积是________；

16．如图，在平面直角坐标系中，将正方形绕点逆时针旋转后得到正方形，依此方式，绕点连续旋转2019次得到正方形，如果点的坐标为（1，0），那么点的坐标为________．

三、解下列各题(本大题共8小题，共72分)

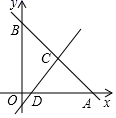
17．（8分）如图，在平面直角坐标系中，OA=OB=8，OD=1，点C为线段AB的中点

(1)直接写出点C的坐标                 ；

(2)求直线CD的解析式；

(3)在平面内是否存在点F，使得以A、C、D、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．

18．（8分）如图、，在平行四边形中，、的角平分线、分别与线段两侧的延长线（或线段）相交与、，与相交于点.

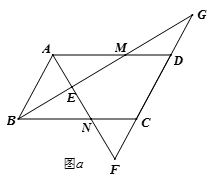
（1）在图中，求证：，.

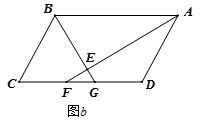
（2）在图中，仍有（1）中的，成立，请解答下面问题：

①若，，，求和的长；

②是否能给平行四边形的边和角各添加一个条件，使得点恰好落在边上且为等腰三角形？若能，请写出所给条件；若不能，请说明理由.

19．（8分）已知正方形中，为对角线上一点，过点作交于点，连接，为的中点，连接．

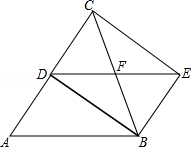
（1）如图1，求证：；

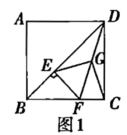
（2）将图1中的绕点逆时针旋转45°，如图2，取的中点，连接．问（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．

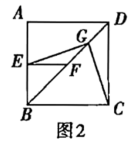
（3）将图1中的绕点逆时计旋转任意角度，如图3，取的中点，连接．问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）

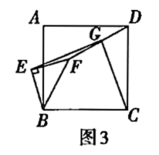
20．（8分）如图，在长方形中，，，动点、分别从点、同时出发，点以2厘米/秒的速度向终点移动，点以1厘米/秒的速度向移动，当有一点到达终点时，另一点也停止运动.设运动的时间为，问：

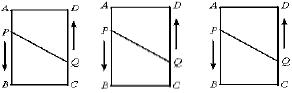
(1)当秒时，四边形面积是多少？

(2)当为何值时，点和点距离是？

(3)当_________时，以点、、为顶点的三角形是等腰三角形.(直接写出答案)

21．（8分）如图，在△ABC中，AB=BC，BD平分∠ABC，四边形ABED是平行四边形，DE交BC于点F，连接CE

求证：四边形BECD是矩形．

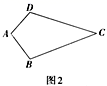
22．（10分）我们把对角线互相垂直的四边形叫做垂美四边形.

(1)（概念理解）在平行四边形、矩形、菱形、正方形中，一定是垂美四边形的是___________.

(2)（性质探究）如图2，试探索垂美四边形ABCD的两组对边AB,CD与BC ，AD之间的数量关系，写出证明过程。

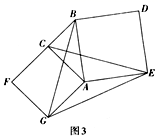
(3)（问题解决）如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外做正方形ACFG和正方形ABDE，连接CE,BG,GE,  已知AC=,BC=1 求GE的长.

23．（10分）如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：

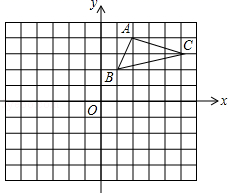
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．

（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．

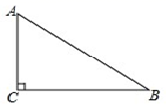
24．（12分）如图，在 ABC ，C  90，AC＜BC，D 为 BC 上一点，且到 A、B 两点的距离相等．

（1）用直尺和圆规，作出点 D 的位置（不写作法，保留作图痕迹）；

（2）连结 AD，若 B  36 ，求∠CAD 的度数．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、D

3、C

4、B

5、D

6、D

7、D

8、B

9、A

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、16

12、

13、

14、2

15、

16、

三、解下列各题(本大题共8小题，共72分)

17、 (1)点C的坐标为(4，4)；(2)直线CD的解析式是y=；(3)点F的坐标是(11，4)，(5，-4)或(-3，4)．

18、（1）见解析；（2）①，，②，，见解析.

19、 (1)见解析;(2)见解析;(3)见解析.

20、（1）5厘米2；（2）秒或秒；（3）秒或秒或秒或秒.

21、证明见解析

22、菱形、正方形

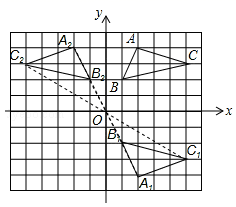
23、解：（1）如图所示：点A1的坐标（2，﹣4）。

（2）如图所示，点A2的坐标（﹣2，4）。

24、 (1)作图见解析；（2）18°