


福建省三明市县2022-2023学年七下数学期末考试试题含答案
展开福建省三明市县2022-2023学年七下数学期末考试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对无锡市空气质量情况的调查 B.对某校七年级(![]() )班学生视力情况的调查
)班学生视力情况的调查
C.对某批次手机屏使用寿命的调查 D.对全国中学生每天体育锻炼所用时间的调查
2.以下列各组数为边长,不能构成直角三角形的是( )
A.3,4,5 B.9,12,15 C.![]() ,2,
,2,![]() D.0.3,0.4,0.5
D.0.3,0.4,0.5
3.某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共有了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.下列四组线段中,可以构成直角三角形的是( )
A.1,2,3 B.4,5,6 C.9,12,15 D.![]()
5.如果![]() ,那么代数式
,那么代数式![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
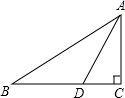
A.3 B.4 C.5 D.6
7.如图,在一个高为6米,长为10米的楼梯表面铺地毯,则地毯长度至少是( )
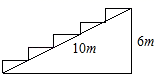
A.6米 B.10米 C.14米 D.16米
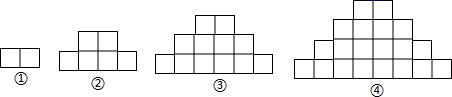
8.如图,每个图形都是由同样大小的正方形按照一定的规律组成,其中第①个图形面积为![]() ,第②个图形的面积为
,第②个图形的面积为![]() ,第③个图形的面积为
,第③个图形的面积为![]() ,…,那么第⑥个图形面积为( )
,…,那么第⑥个图形面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在平行四边形ABCD中,![]() ,
,![]() .则平行四边形ABCD的周长是( ).
.则平行四边形ABCD的周长是( ).
A.16 B.13 C.10 D.8
10.下列各点中在函数y=2x+2的图象上的是( )
A.(1,-2) B.(-1,-1) C.(0,2) D.(2,0)
11.如图,已知△ABC,按以下步骤作图:①分别以B、C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为( )
BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为( )
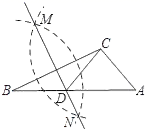
A.65° B.60° C.55° D.45°
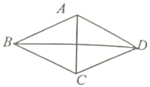
12.如图,菱形![]() 中,
中,![]() ,这个菱形的周长是( )
,这个菱形的周长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是_________.

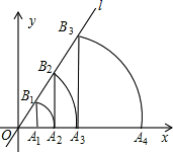
14.在直角坐标系中,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3…按照这样的作法进行下去,则点A20的坐标是______.
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3…按照这样的作法进行下去,则点A20的坐标是______.
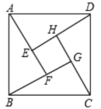
15.赵爽(约公元182~250年),我国历史上著名的数学家与天文学家,他详细解释了《周髀算经》中勾股定理,将勾股定理表述为:“勾股各自乘,并之为弦实.开方除之,即弦.”又给出了新的证明方法“赵爽弦图”,巧妙地利用平面解析几何面积法证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形,如果小正方形的面积为1,直角三角形较长直角边长为4,则大正方形的面积为_____________________.
16.若分式 ![]() 的值为零,则x=________.
的值为零,则x=________.
17.方程![]() 的解是__________.
的解是__________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)计算:![]() +(
+(![]() ﹣1)2﹣
﹣1)2﹣![]()
19.(5分)函数y=mx+n与y=nx的大致图象是( )
A.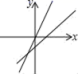 B.
B.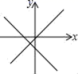
C.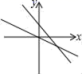 D.
D.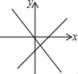
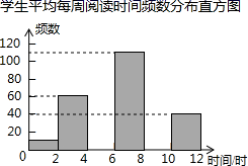
20.(8分)为引导学生广泛阅读古今文学名著,某校开展了读书活动.学生会随机调查了部分学生平均每周阅读时间的情况,整理并绘制了如下的统计图表:
学生平均每周阅读时间频数分布表
平均每周阅读时间x(时) | 频数 | 频率 |
0≤x<2 | 10 | 0.025 |
2≤x<4 | 60 | 0.150 |
4≤x<6 | a | 0.200 |
6≤x<8 | 110 | b |
8≤x<10 | 100 | 0.250 |
10≤x≤12 | 40 | 0.100 |
合计 | 400 | 1.000 |
请根据以上信息,解答下列问题;
(1)在频数分布表中,a=______,b=______;
(2)补全频数分布直方图;
(3)如果该校有1600名学生,请你估计该校平均每周阅读时间不少于6小时的学生大约有多少人?
21.(10分)某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
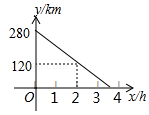
22.(10分)甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60km/h.
(1)求甲车的速度;
(2)当甲乙两车相遇后,乙车速度变为a(km/h),并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求a的值.
23.(12分)已知:如图,在菱形ABCD中, BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.

(1)判断四边形EBCF的形状,并证明;
(2)若AF=9,CF=3,求CD的长.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、C
3、B
4、C
5、A
6、A
7、C
8、C
9、A
10、C
11、A
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、AC⊥BD
14、(219,0)
15、1
16、2
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、1
19、D
20、(1)80,0.1;(2)见详解;(3)1000人
21、该商品每个定价为1元,进货100个.
22、(1)80km/h;(2)1.
23、(1)四边形EBCF是矩形,证明见解析;(2)CD =5
福建省三明市县2023-2024学年数学九年级第一学期期末考试模拟试题含答案: 这是一份福建省三明市县2023-2024学年数学九年级第一学期期末考试模拟试题含答案,共8页。试卷主要包含了二次函数图象如图,下列结论,在平面直角坐标系中,点P,若,那么的值是,观察下列等式等内容,欢迎下载使用。
2023-2024学年福建省三明市县八年级数学第一学期期末达标检测模拟试题含答案: 这是一份2023-2024学年福建省三明市县八年级数学第一学期期末达标检测模拟试题含答案,共7页。试卷主要包含了如图,在中,,,则的度数为,下列各式计算正确的是等内容,欢迎下载使用。
福建省三明市永安市2022-2023学年七下数学期末监测试题含答案: 这是一份福建省三明市永安市2022-2023学年七下数学期末监测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,已知,下列各式中,正确的是,要使分式有意义,应满足的条件是等内容,欢迎下载使用。












