


湖南长沙市南雅中学2022-2023学年数学七下期末达标检测模拟试题含答案
展开湖南长沙市南雅中学2022-2023学年数学七下期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如图,点![]() 、
、![]() 在函数
在函数![]() (
(![]() ,
,![]() 且
且![]() 是常数)的图像上,且点
是常数)的图像上,且点![]() 在点
在点![]() 的左侧过点
的左侧过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() 、
、![]() .若
.若![]() 和
和![]() 的面积分别为1和4,则
的面积分别为1和4,则![]() 的值为( )
的值为( )
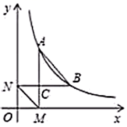
A.4 B.![]() C.
C.![]() D.6
D.6
2.下列说法正确的是( )
A.了解某型导弹杀伤力的情况应使用全面调查
B.一组数据3、6、6、7、9的众数是6
C.从2000名学生中选200名学生进行抽样调查,样本容量为2000
D.甲、乙两人在相同的条件下各射击10次,他们成绩的平均数相同,方差分别是S2甲=0.3,S2乙=0.4,则乙的成绩更稳定
3.如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
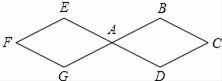
A.点F B.点E C.点A D.点C
4.如图,已知菱形ABCD的周长是24米,∠BAC=30°,则对角线BD的长等于()
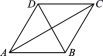
A.6![]() 米 B.3
米 B.3![]() 米 C.6米 D.3米
米 C.6米 D.3米
5.为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把5m长的彩绳截成2m或1m的彩绳,用来做手工编织,在不造成浪费的前提下,你有几种不同的截法( )
A.4 B.3 C.2 D.1
6.下列四边形中,对角线相等且互相垂直平分的是( )
A.平行四边形 B.正方形 C.等腰梯形 D.矩形
7.若A(a,3),B(1,b)关于x轴对称,则a+b=( )
A.2 B.-2 C.4 D.-4
8.不等式2x-1≤3的解集是( )
A.x≤1 B.x≤2 C.x≥1 D.x≤-2
9.若![]() 的函数值
的函数值![]() 随着
随着![]() 的增大而增大,则
的增大而增大,则![]() 的值可能是( )
的值可能是( )
A.0 B.1 C.-3 D.-2
10.若![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知关于x的方程x2-2ax+1=0有两个相等的实数根,则a=____.
12.已知三角形的三条中位线的长分别为5cm、6cm、10cm,则这个三角形的周长是_____cm.
13.若![]() ,则
,则![]() 的取值范围是_________.
的取值范围是_________.
14.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是_________.
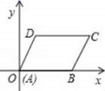
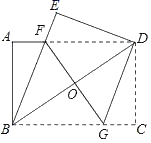
15.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG∥BE,交BC于点G,连接FG交BD于点O.若AB=6,AD=8,则DG的长为_____.
16.已知![]() ,则
,则![]() 的值是_______.
的值是_______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)我市遗爱湖公园内有一块四边形空地,如图所示,景区管理人员想在这块空地上铺满观赏草坪,需要测量其面积.经技术人员测量,![]() ,
,![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() 米.
米.
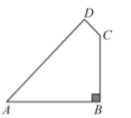
(1)请你帮助管理人员计算出这个四边形对角线![]() 的长度;
的长度;
(2)请用你学过的知识帮助管理员计算出这块空地的面积.
18.(8分)师徒两人分别加工1200个零件,已知师傅每天加工零件的个数是徒弟每天加工零件个数的1.5倍,结果师傅比徒弟少用10天完成,求徒弟每天加工多少个零件?
19.(8分)如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,把点
,把点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() .过点
.过点![]() 且与
且与![]() 平行的直线交
平行的直线交![]() 轴于点
轴于点![]() .
.
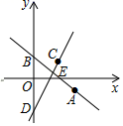
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
20.(8分)用适当的方法解下列方程:
(1)x(2﹣x)=x2﹣2
(2)(2x+5)2﹣3(2x+5)+2=0
21.(8分)已知![]() 是不等式
是不等式![]() 的一个负整数解,请求出代数式
的一个负整数解,请求出代数式![]()
![]() 的值.
的值.
22.(10分)如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达地点B相距50米,结果他在水中实际游的路程比河的宽度多10米,求该河的宽度AB为多少米?
23.(10分)如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
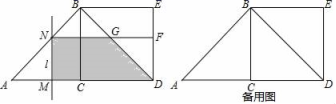
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
24.(12分)在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):
方案一:提供8000元赞助后,每张票的票价为50元;
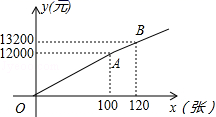
方案二:票价按图中的折线OAB所表示的函数关系确定.
(1)若购买120张票时,按方案一和方案二分别应付的购票款是多少?
(2)求方案二中y与x的函数关系式;
(3)至少买多少张票时选择方案一比较合算?
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、A
4、C
5、B
6、B
7、B
8、B
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、1
13、a≤3
14、 (7,3)
15、![]()
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)25米;(2)234米2
18、徒弟每天加工40个零件.
19、(1)y=3x-10;(2)![]()
20、(1)x1=![]() ,x1=
,x1=![]() ;(1)x1=﹣
;(1)x1=﹣![]() ,x1=﹣1.
,x1=﹣1.
21、![]() ,原式
,原式![]()
22、1200米
23、(1)BN=2![]() ﹣
﹣![]() t;(2)当t=4﹣
t;(2)当t=4﹣![]() 或t=3或t=2时,△DNE是等腰三角形;(3)当t=
或t=3或t=2时,△DNE是等腰三角形;(3)当t=![]() 时,S取得最大值
时,S取得最大值![]() .
.
24、 (1)14000,13200; (2)y=60x+1.(3)200.
湖南长沙市南雅中学2023-2024学年九上数学期末监测模拟试题含答案: 这是一份湖南长沙市南雅中学2023-2024学年九上数学期末监测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,反比例函数y=的图象位于,关于抛物线y=3,下列说法正确的是等内容,欢迎下载使用。
2023-2024学年湖南长沙市南雅中学八上数学期末质量跟踪监视模拟试题含答案: 这是一份2023-2024学年湖南长沙市南雅中学八上数学期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了若的结果中不含项,则的值为等内容,欢迎下载使用。
2023-2024学年湖南省长沙市南雅中学数学八上期末监测模拟试题含答案: 这是一份2023-2024学年湖南省长沙市南雅中学数学八上期末监测模拟试题含答案,共7页。试卷主要包含了已知x-y=3,,则的值等于,已知,,则的值为,2 的平方根是等内容,欢迎下载使用。












