


湖北省武汉市蔡甸区2022-2023学年七年级数学第二学期期末质量检测试题含答案
展开这是一份湖北省武汉市蔡甸区2022-2023学年七年级数学第二学期期末质量检测试题含答案,共7页。试卷主要包含了化简的结果是,已知,则的值为等内容,欢迎下载使用。
湖北省武汉市蔡甸区2022-2023学年七年级数学第二学期期末质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如果点P(-2,b)和点Q(a,-3)关于x轴对称,则![]() 的值是( )
的值是( )
A.1 B.-1 C.5 D.-5
2.如果![]() ,那么代数式
,那么代数式![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若y关于x的函数y=(m-2)x+n是正比例函数,则m,n应满足的条件是( )
A.m≠2且n=0 B.m=2且n=0 C.m≠2 D.n=0
4.如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,连接DE,EF,DF,则下列说法不正确的是( )
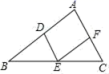
A.S△DEF=![]() S△ABC
S△ABC
B.△DEF≌△FAD≌△EDB≌△CFE
C.四边形ADEF,四边形DBEF,四边形DECF都是平行四边形
D.四边形ADEF的周长=四边形DBEF的周长=四边形DECF的周长
5.化简![]() 的结果是( )
的结果是( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
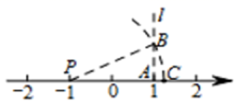
6.如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为1,过点
表示的数为1,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作弧,弧与数轴的交点
为半径作弧,弧与数轴的交点![]() 所表示的数为( )
所表示的数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知一组数据为8,9,10,10,11,则这组数据的众数( )
A.8 B.9 C.10 D.11
8.关于![]() 的方程
的方程![]() 有实数解,那么
有实数解,那么![]() 的取值范围是()
的取值范围是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 且
且![]()
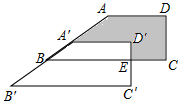
9.如图,在四边形ABCD中,AD∥BC,∠BCD=90°,将四边形ABCD沿AB方向平移得到四边形A'B'C'D',BC与C'D'相交于点E,若BC=8,CE=3,C'E=2,则阴影部分的面积为( )
A.12+2![]() B.13 C.2
B.13 C.2![]() +6 D.26
+6 D.26
10.已知![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
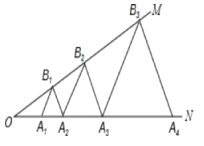
11.如图,已知:∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为____
的边长为____
12.一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是___.
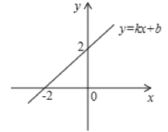
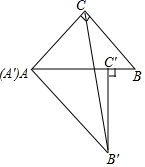
13.如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在AB上,连接B′C,若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为____.
14.已知![]() ,
,![]() 为实数,且满足
为实数,且满足![]() ,则
,则![]() _____.
_____.
15.若![]() ,化简
,化简![]() 的正确结果是________________.
的正确结果是________________.
16.若二次根式![]() 有意义,则
有意义,则![]() 的取值范围是________.
的取值范围是________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某村深入贯彻落实新时代中国特色社会主义思想,认真践行“绿水青山就是金山银山”理念在外打工的王大叔返回江南创业,承包了甲乙两座荒山,各栽100棵小枣树,发现成活率均为97%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的小枣,每棵的产量如折线统计图所示.
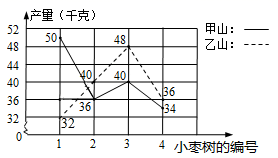
(1)直接写出甲山4棵小枣树产量的中位数;
(2)分别计算甲乙两座小枣样本的平均数,并判断那座山的样本的产量高;
(3)用样本平均数估计甲乙两座山小枣的产量总和.
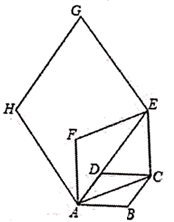
18.(8分)如图,边长为1的菱形![]() 中,
中,![]() ,连结对角线
,连结对角线![]() ,以
,以![]() 为边作第二个菱形
为边作第二个菱形![]() ,使
,使![]() ,连结
,连结![]() ,再以
,再以![]() 为边作第三个菱形
为边作第三个菱形![]() 使
使![]() …按此规律所作的第2019个菱形的边长是__________.
…按此规律所作的第2019个菱形的边长是__________.
19.(8分)求证:一组对边平行且相等的四边形是平行四边形.(要求:画出图形,写出已知、求证和证明过程)
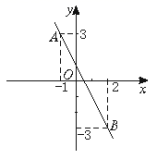
20.(8分)如图一次函数y=kx+b的图象经过点A和点B.
(1)写出点A和点B的坐标并求出k、b的值;
(2)求出当x=![]() 时的函数值.
时的函数值.
21.(8分)完成下列运算
(1)计算:![]()
(2)计算:![]()
(3)计算:![]()
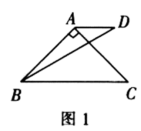
22.(10分)问题提出:
(1)如图1,在![]() 中,
中,![]() ,点D和点A在直线
,点D和点A在直线![]() 的同侧,
的同侧,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,将
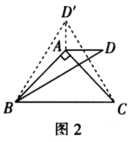
,将![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() (如图2),可求出
(如图2),可求出![]() 的度数为______.
的度数为______.
问题探究:
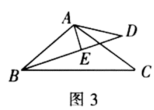
(2)如图3,在(1)的条件下,若![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
①求![]() 的度数.
的度数.
②过点A作直线![]() ,交直线
,交直线![]() 于点E,
于点E,![]() .请求出线段
.请求出线段![]() 的长.
的长.
23.(10分)如图,在正方形ABCD中,E、F是对角线BD上两点,将![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() 后,得到
后,得到![]() ,连接EM,AE,且使得
,连接EM,AE,且使得![]() .
.
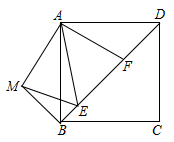
(1)求证:![]() ;(2)求证:
;(2)求证:![]() .
.
24.(12分)小李在学校“青少年科技创新比赛”活动中,设计了一个沿直线轨道做匀速直线运动的模型.甲车从![]() 处出发向
处出发向![]() 处行驶,同时乙车从
处行驶,同时乙车从![]() 处出发向
处出发向![]() 处行驶.如图所示,线段
处行驶.如图所示,线段![]() 、
、![]() 分别表示甲车、乙车离
分别表示甲车、乙车离![]() 处的距离
处的距离![]() (米)与已用时间
(米)与已用时间![]() (分)之间的关系.试根据图象,解决以下问题:
(分)之间的关系.试根据图象,解决以下问题:
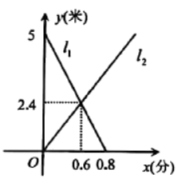
(1)填空:出发_________(分)后,甲车与乙车相遇,此时两车距离![]() 处________(米);
处________(米);
(2)求乙车行驶![]() (分)时与
(分)时与![]() 处的距离.
处的距离.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、D
3、A
4、D
5、B
6、B
7、C
8、B
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、32
12、x<−2.
13、3![]()
14、4
15、1.
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)38;(2)![]() ,
,![]() ,甲山样本的产量高;(3)甲乙两山小枣的产量总和为7663千克.
,甲山样本的产量高;(3)甲乙两山小枣的产量总和为7663千克.
18、![]()
19、见解析.
20、.(1)k=-1,b=1 (1)-1
21、(1)![]() (2)1;(3)
(2)1;(3)![]()
22、(1)30°;(2)①![]() ;②
;②![]()
23、(1)见解析;(2)见解析.
24、(1)0.6,2.4;(2)4.8米
相关试卷
这是一份湖北省武汉市蔡甸区2023-2024学年数学九上期末达标检测试题含答案,共7页。试卷主要包含了如图,在中,,则等于等内容,欢迎下载使用。
这是一份湖北省武汉市蔡甸区求新联盟2023-2024学年九上数学期末达标检测模拟试题含答案,共7页。试卷主要包含了已知二次函数,下列四对图形中,是相似图形的是,函数y=3等内容,欢迎下载使用。
这是一份2023-2024学年湖北省武汉市蔡甸区八年级上学期期中数学质量检测试题,共7页。试卷主要包含了本试卷由和两部分组成,认真阅读答题卡上的注意事项等内容,欢迎下载使用。












