


河南省郸城县2022-2023学年数学七年级第二学期期末达标检测试题含答案
展开河南省郸城县2022-2023学年数学七年级第二学期期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.一天早上小华步行上学,他离开家后不远便发现数学书忘在了家里,于是以相同的速度回家去拿,到家后发现弟弟把牛奶洒在了地上,就放下手中的东西,收拾好后才离开.为了不迟到,小华跑步到了学校,则小华离学校的距离y与时间t之间的函数关系的大致图象是( )
A.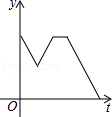 B.
B.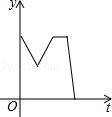 C.
C.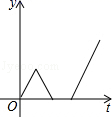 D.
D.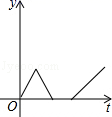
2.某校艺术节的乒乓球比赛中,小东同学顺利进入决赛.有同学预测“小东夺冠的可能性是80%”,则对该同学的说法理解最合理的是( )
A.小东夺冠的可能性较大 B.如果小东和他的对手比赛10局,他一定会赢8局
C.小东夺冠的可能性较小 D.小东肯定会赢
3.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有( )

A.0个 B.1个 C.2个 D.3个
4.分式![]() 有意义的条件是( )
有意义的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列各式由左到右的变形中,属于因式分解的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.如果关于x的一次函数y=(a+1)x+(a﹣4)的图象不经过第二象限,且关于x的分式方程![]() 有整数解,那么整数a值不可能是( )
有整数解,那么整数a值不可能是( )
A.0 B.1 C.3 D.4
7.如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
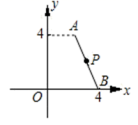
A.(3,2) B.(6,2) C.(6,4) D.(3,5)
8.如图,在周长为 18cm 的▱ABCD 中,AC、BD 相交于点 O,OE⊥BD 交 AD 于 E,则△ABE的周长为( )
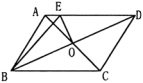
A.6cm B.7cm
C.8cm D.9cm
9.在平面直角坐标系中,一次函数y=x﹣1和y=﹣x+1的图象与x轴的交点及x轴上方的部分组成的图象可以表示为函数y=|x﹣1|,当自变量﹣1≤x≤2时,若函数y=|x﹣a|(其中a为常量)的最小值为a+5,则满足条件的a的值为( )
A.﹣3 B.﹣5 C.7 D.﹣3或﹣5
10.下列二次根式化简的结果正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.化简:![]() ______.
______.
12.![]() 的化简结果为________
的化简结果为________
13.若![]() ,则
,则![]() 的值是________.
的值是________.
14.如图,在▱ABCD中,若∠A=63°,则∠D=_____.
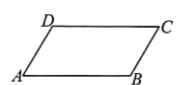
15.若关于x的方程x2+mx-3=0有一根是1,则它的另一根为________.
16.不等式组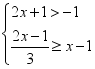 的整数解有_____个.
的整数解有_____个.
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知函数y=x+![]() (x>0),它的图象犹如老师的打钩,因此人称对钩函数.下表是y与x的几组对应值:
(x>0),它的图象犹如老师的打钩,因此人称对钩函数.下表是y与x的几组对应值:
x |
|
|
| 1 | 2 | 3 | 4 |
y | 4 | 3 | 2 | 2 | 2 | 3 | 4 |
请你根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究.
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
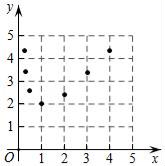
(2)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x=1右侧,函数图象呈上升状态 | 当x>1时,y随x的增大而增大 |
示例2 | 函数图象经过点(2,2 | 当x=2时,y=2 |
① | 函数图象的最低点是(1,2) |
|
② | 在直线x=1左侧,函数图象呈下降状态 |
|
(3)当a≤x≤4时,y的取值范围为2≤y≤4![]() ,则a的取值范围为 .
,则a的取值范围为 .
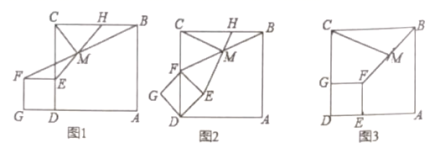
18.(8分)如图1,点![]() 是正方形
是正方形![]() 边
边![]() 上任意一点,以
上任意一点,以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 中点,射线
中点,射线![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)请直接写出![]() 和
和![]() 的数量关系和位置关系.
的数量关系和位置关系.
(2)把图1中的正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,此时点
,此时点![]() 恰好落在线段
恰好落在线段![]() 上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由.
上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由.
(3)把图1中的正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,此时点
,此时点![]() 、
、![]() 恰好分别落在线段
恰好分别落在线段![]() 、
、![]() 上,连接
上,连接![]() ,如图3,其他条件不变,若
,如图3,其他条件不变,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长度.
的长度.
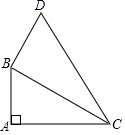
19.(8分)如图,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=1.
(1)连接BC,求BC的长;
(2)求△BCD的面积.
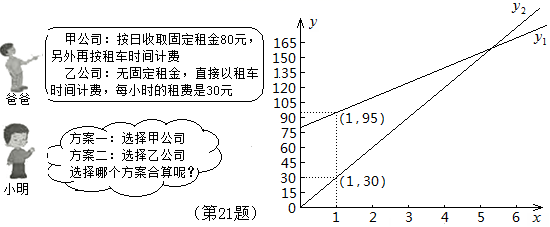
20.(8分) “五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
21.(8分)求不等式组![]() 的整数解.
的整数解.
22.(10分)如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ;直线
;直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,已知关于
,已知关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() .
.
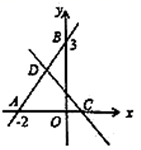
(1)分别求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() .
.
23.(10分)如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是1.
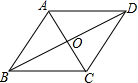
求:(1)两条对角线的长度;(2)菱形的面积.
24.(12分)解不等式组: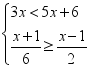 ,把它的解集在数轴上表示出来,并写出其整数解.
,把它的解集在数轴上表示出来,并写出其整数解.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、D
4、B
5、C
6、B
7、B
8、D
9、A
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、3
12、![]()
13、1
14、117°
15、-1
16、3
三、解下列各题(本大题共8小题,共72分)
17、(1)画图见解析;(2):x=1时,y有最小值2,当x<1时,y随x的增大而减小;(3)1≤a≤4
18、(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
19、(1)BC=15;(2)S△BCD=2.
20、(1)y1=15x+80(x≥0);y2=30x(x≥0);(2)当租车时间为![]() 小时,选择甲乙公司一样合算;当租车时间小于
小时,选择甲乙公司一样合算;当租车时间小于![]() 小时,选择乙公司合算;当租车时间大于
小时,选择乙公司合算;当租车时间大于![]() 小时,选择甲公司合算.
小时,选择甲公司合算.
21、-1、-1、0、1 、1.
22、(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]()
23、(1)AC=8,BD=![]() ;(2)
;(2)![]() .
.
24、![]() ,x的整数解为﹣1,﹣1,0,1,1.
,x的整数解为﹣1,﹣1,0,1,1.
河南省周口川汇区2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案: 这是一份河南省周口川汇区2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案,共6页。试卷主要包含了方程x等内容,欢迎下载使用。
河南省焦作市温县2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案: 这是一份河南省焦作市温县2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,只用下列图形不,在圆的周长公式中,常量是等内容,欢迎下载使用。
2022-2023学年河南省新乡、开封市名校联考数学七年级第二学期期末达标检测模拟试题含答案: 这是一份2022-2023学年河南省新乡、开封市名校联考数学七年级第二学期期末达标检测模拟试题含答案,共6页。












