


江苏省睢宁县2022-2023学年七下数学期末质量跟踪监视试题含答案
展开江苏省睢宁县2022-2023学年七下数学期末质量跟踪监视试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )
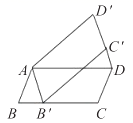
A.60° B.65° C.70° D.75°
2.在平行四边形ABCD中,若∠A+∠C=260°,则∠D的度数为( )
A.120° B.100° C.50° D.130°
3.下列计算错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() 于
于![]() ,则
,则![]() =( )
=( )
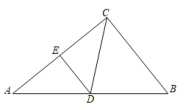
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
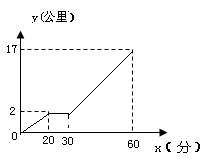
A.小强从家到公共汽车在步行了2公里 B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时 D.小强乘公共汽车用了20分钟
6.在平而直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则关于点D的说法正确的是( )
甲:点D在第一象限
乙:点D与点A关于原点对称
丙:点D的坐标是(-2,1)
丁:点D与原点距离是![]() .
.
A.甲乙 B.乙丙 C.甲丁 D.丙丁
7.在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可![]() 能是( )
能是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如图,□ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
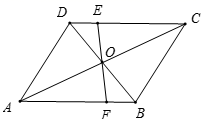
A.8.3 B.9.6 C.12.6 D.13.6
9.下列运算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.13名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前6名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )
A.方差 B.众数 C.平均数 D.中位数
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如果一组数据x1,x2,…,xn的方差是4,则另一组数据x1+3,x2+3,…,xn+3的方差是_____.
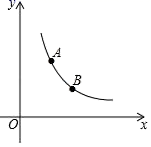
12.如图,已知点A(1,a)与点B(b,1)在反比例函数y=![]() (x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是______.
(x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是______.
13.D、E、F分别是△ABC各边的中点.若△ABC的周长是12cm,则△DEF的周长是____cm.
14.抛物线![]() 有最_______点.
有最_______点.
15.已知一次函数![]() 的图像经过点
的图像经过点![]() ,那么这个一次函数在
,那么这个一次函数在![]() 轴上的截距为__________.
轴上的截距为__________.
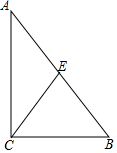
16.如图,在![]() 中,若
中,若![]() ,点
,点![]() 是
是![]() 的中点,则
的中点,则![]() _____.
_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某景点的门票零售价为80元/张,“五一”黄金周期间,甲乙两家旅行社推出优惠活动,甲旅行社一律九折优惠;乙旅行社对10人以内(含10人)不优惠,超过10人超出部分八折优惠,某班部分同学去该景点旅游.设参加旅游人数为x人,购买门票需要y元.
(1)分别直接写出两家旅行社y与x的函数关系式,并写出对应自变量x的取值范围;
(2)请根据该班旅游人数设计最省钱的购票方案.
18.(8分)在△ABC中,∠C=90°,AB=20,若∠A=60°,求BC,AC的长.
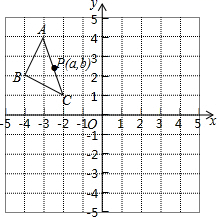
19.(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称.
(1)画出△A1B1C1,并写出点A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对应点为P'(a+3,b+1),请画出平移后的△A2B2C2.
20.(8分)如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
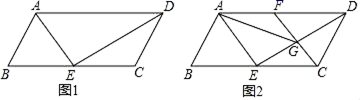
(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
21.(8分)在平面直角坐标系![]() 中,直线
中,直线![]() (
(![]() 且
且![]() )与
)与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作直线
作直线![]() 轴,且与
轴,且与![]() 交于点
交于点![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(2)若![]() ,
,![]() ,且
,且![]() 轴,判断四边形
轴,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
22.(10分)某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件,可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排![]() 名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.
名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.
(1)请写出此车间每天所获利润![]() (元)与
(元)与![]() (人)之间的函数关系式;
(人)之间的函数关系式;
(2)求自变量![]() 的取值范围;
的取值范围;
(3)怎样安排生产每天获得的利润最大,最大利润是多少?
23.(10分)解方程组:![]() .
.
24.(12分)已知A.B两地果园分别有苹果30吨和40吨,C.D两地的农贸市场分别需求苹果20吨和50吨。已知从A.B两地到C.D两地的运价如表:
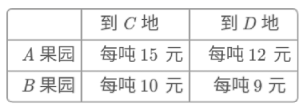
(1)填空:若从A果园运到C地的苹果为10吨,则从A果园运到D地的苹果为___吨,从B果园运到C地的苹果为___吨,从B果园运到D地的苹果为___吨,总运输费为___元;
(2)如果总运输费为750元时,那么从A果园运到C地的苹果为多少吨?
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、D
4、C
5、D
6、D
7、A
8、B
9、D
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、﹣1或3
13、1
14、低
15、1
16、1
三、解下列各题(本大题共8小题,共72分)
17、 (1)见解析;(2)见解析.
18、![]()
19、(1)作图见解析,A1的坐标是(3,-4);(2)作图见解析.
20、(1)见解析;(2)①t=3(秒);②AG=![]() .
.
21、(1)BC=1;(2)四边形OBDA是平行四边形,见解析.
22、(1)![]() ;(2)
;(2)![]() (3)安排13人生产甲种零件,安排7人生产乙种零件,所获利润最大,最大利润为20800元.
(3)安排13人生产甲种零件,安排7人生产乙种零件,所获利润最大,最大利润为20800元.
23、 ,
,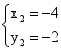
24、(1)20,10,30,760;(2)从A果园运到C地的苹果数为5吨
江苏省盱眙县2022-2023学年七下数学期末质量跟踪监视模拟试题含答案: 这是一份江苏省盱眙县2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了小勇投标训练4次的成绩分别是,下列函数中,是的正比例函数的是,用配方法解方程,则方程可变形为,如果方程有增根,那么k的值等内容,欢迎下载使用。
江苏省沭阳县联考2022-2023学年数学七下期末质量跟踪监视试题含答案: 这是一份江苏省沭阳县联考2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了若分式 的值为0,则的值等于,直线y=﹣x+1不经过等内容,欢迎下载使用。
山东泰安2022-2023学年数学七下期末质量跟踪监视试题含答案: 这是一份山东泰安2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了一元二次方程的根是,整数满足,则的值为等内容,欢迎下载使用。












