


江苏省泰兴市黄桥东区域2022-2023学年数学七年级第二学期期末考试试题含答案
展开江苏省泰兴市黄桥东区域2022-2023学年数学七年级第二学期期末考试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.![]() 的算术平方根是( )
的算术平方根是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶.已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需( )分钟到达终点B.
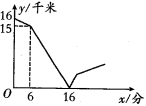
A.78 B.76 C.16 D.12
3.分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,最简分式的个数有( )
中,最简分式的个数有( )
A.1个 B.2个 C.3个 D.4个
4.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<1;②a>1;③当x<4时,y1<y2;④b<1.其中正确结论的个数是( )
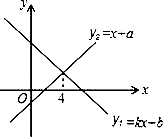
A.4个 B.3个 C.2个 D.1个
5.如图,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 、
、![]() 相交于点O,
相交于点O,![]() 于点E,
于点E,![]() 于点F,连接
于点F,连接![]() 、
、![]() ,若
,若![]() ,则下列结论不一定正确的是( )
,则下列结论不一定正确的是( )
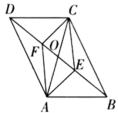
A.![]() B.
B.![]() C.
C.![]() 为直角三角形 D.四边形
为直角三角形 D.四边形![]() 是平行四边形
是平行四边形
6.一个不透明的袋子中装有21个红球和若干个白球,这些球除了颜色外都相同,若小英每次从袋子中随机摸出一个球,记下颜色后再放回,经过多次重复试验,小英发现摸到红球的频率逐渐稳定于1.4,则小英估计袋子中白球的个数约为( )
A.51 B.31 C.12 D.8
7.如图,□ABCD中,∠C=100°,BE平分∠ABC,则∠AEB的度数为( )
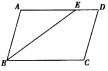
A.60° B.50° C.40° D.30°
8.解不等式![]() ,解题依据错误的是( )
,解题依据错误的是( )
解:①去分母,得5(x+2)<3(2x﹣1)
②去括号,得5x+10<6x﹣3
③移项,得5x﹣6x<﹣3﹣1![]() 0
0
④合并同类项,得﹣x<﹣13
⑤系数化1,得x>13
A.②去括号法则 B.③不等式的基本性质1
C.④合并同类项法则 D.⑤不等式的基本性质2
9.某人出去散步,从家里出发,走了20min,到达一个离家900m的阅报亭,看了10min报纸后,用了15min返回家里,下面图象中正确表示此人离家的距离y(m)与时间x(min)之家关系的是( )
A.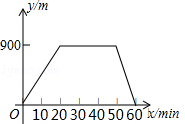 B.
B.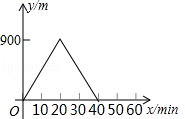
C.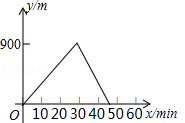 D.
D.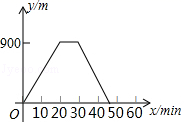
10.下列属于矩形具有而菱形不具有的性质是( )
A.两组对边分别平行且相等
B.两组对角分别相等
C.对角线相互平分
D.四个角都相等
11.如图,将矩形ABCD的四个角向内折叠铺平,恰好拼成一个无缝隙无重叠的矩形EFGH,若EH=5,EF=12,则矩形ABCD的面积是( )
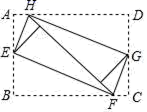
A.13 ![]() B.
B.![]()
![]() C.60
C.60 ![]() D.120
D.120
12.如图,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,则方程组
,则方程组![]() 解是( )
解是( )
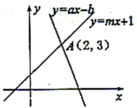
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围为____.
的取值范围为____.
14.若函数y=(m+1)x+(m2-1) (m为常数)是正比例函数,则m的值是____________。
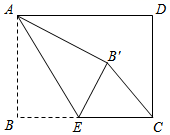
15.如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处.当
处.当![]() 为直角三角形时,
为直角三角形时,![]() __.
__.
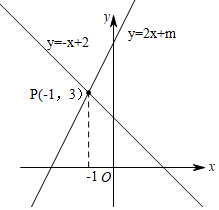
16.如图,已知一次函数![]() 与y=2x+m的图象相交于
与y=2x+m的图象相交于![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集是__.
的解集是__.
17.如图,在![]() 中,
中,![]() 为边
为边![]() 上一点,以
上一点,以![]() 为边作矩形
为边作矩形![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为______度.
的大小为______度.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图所示,直线y=-![]() x+8与x轴、y轴分别相交于点A,B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.
x+8与x轴、y轴分别相交于点A,B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.
求:(1)点B′的坐标;
(2)直线AM所对应的函数表达式.

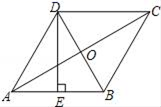
19.(5分)如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=4![]() ,求DE的长.
,求DE的长.
20.(8分)解方程:(1)![]() =
=![]() ;
;
(2)![]() -1=
-1=![]() .
.
21.(10分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 坐标为
坐标为![]() .
.
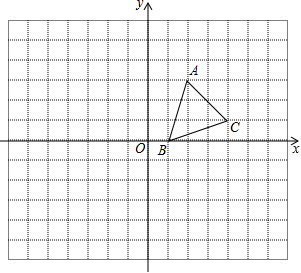
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)画出将![]() 绕原点
绕原点![]() 逆时针旋转90°所得的
逆时针旋转90°所得的![]() ;
;
(3)![]() 与
与![]() 能组成轴对称图形吗?若能,请你画出所有的对称轴.
能组成轴对称图形吗?若能,请你画出所有的对称轴.
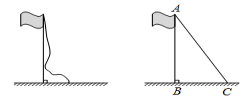
22.(10分)数学综合实验课上,同学们在测量学校旗杆的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开8米后,下端刚好接触地面,如图,根据以上数据,同学们准确求出了旗杆的高度,你知道他们是如何计算出来的吗?
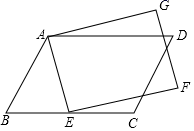
23.(12分)已知四边形![]() ,
,![]() ,
,![]() 与
与![]() 互补,以点
互补,以点![]() 为顶点作一个角,角的两边分别交线段
为顶点作一个角,角的两边分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,试探究:线段
,试探究:线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
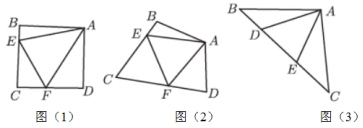
(1)如图(1),当![]() 时,
时,![]() ,
,![]() ,
,![]() 之间的数量关系为___________.
之间的数量关系为___________.
(2)在图(2)的条件下(即不存在![]() ),线段
),线段![]() ,
,![]() ,
,![]() 之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
(3)如图(3),在腰长为![]() 的等腰直角三角形
的等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、A
3、B
4、D
5、C
6、B
7、C
8、D
9、D
10、D
11、D
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、2
15、![]() 或1
或1
16、x>-1
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)点B′的坐标为(-4,0);(2)直线AM的函数表达式为y=-![]() x+3.
x+3.
19、(1)![]() ;(2)
;(2)![]() .
.
20、(1)x=2![]() -2(2)无解
-2(2)无解
21、(1)见解析;(2)见解析;(3)能,图见解析;
22、旗杆的高度为12米.
23、(1)![]() ;(2)成立;证明见解析;(3)
;(2)成立;证明见解析;(3)![]() .
.
江苏省泰兴市黄桥东区域2023-2024学年九上数学期末复习检测试题含答案: 这是一份江苏省泰兴市黄桥东区域2023-2024学年九上数学期末复习检测试题含答案,共8页。试卷主要包含了若,,则的值为,在中,,,若,则的长为等内容,欢迎下载使用。
2023-2024学年江苏省泰兴市黄桥中学数学九上期末考试试题含答案: 这是一份2023-2024学年江苏省泰兴市黄桥中学数学九上期末考试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列事件,在下列函数图象上任取不同两点P,如图,点,,都在上,,则等于等内容,欢迎下载使用。
江苏省泰兴市黄桥集团2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案: 这是一份江苏省泰兴市黄桥集团2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,如图,中,平分,则等于等内容,欢迎下载使用。












