


广西壮族自治区南宁市2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案
展开广西壮族自治区南宁市2022-2023学年七年级数学第二学期期末学业水平测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
2.交警在一个路口统计的某个时段来往车辆的分布如条形图所示.请找出这些车辆速度的众数、中位数分别是( )
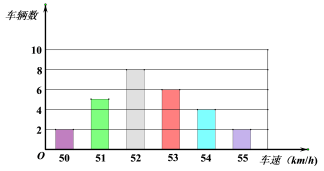
A.52,53 B.52,52 C.53,52 D.52, 51
3.已知点M(1-a,a +2)在第二象限,则a的取值范围是( )
A.a>-2 B.-2<a<1 C.a<-2 D.a>1
4.如图,在正方形ABCD中,AB=10,点E、F是正方形内两点,AE=FC=6,BE=DF=8,则EF的长为( )
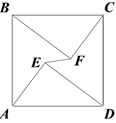
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
5.美是一种感觉,本应没有什么客观的标准,但在自然界里,物体形状的比例却提供了在的称与协调上的一种美感的参考,在数学上,这个比例称为黄金分割.在人体由脚底至肚脐的长度与身高的比例上,肚脐是理想的黄金分割点,也就是说,若此比值越接近![]() 就越给别人一种美的感觉. 某女士身高为
就越给别人一种美的感觉. 某女士身高为![]() ,脚底至肚脐的长度与身高的比为
,脚底至肚脐的长度与身高的比为![]() 为了追求美,地想利用高跟鞋达到这一效果 ,那么她选的高跟鞋的高度约为( )
为了追求美,地想利用高跟鞋达到这一效果 ,那么她选的高跟鞋的高度约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )
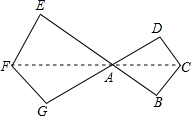
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9
7.直线![]() 不经过【 】
不经过【 】
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.如图,在△ABC中,AB=AC,∠A=36°,以点B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD的度数是( )
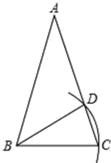
A.18° B.36° C.72° D.108°
9.一次函数y=-kx+k与反比例函数y=-![]() (k≠0)在同一坐标系中的图象可能是( )
(k≠0)在同一坐标系中的图象可能是( )
A.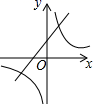 B.
B.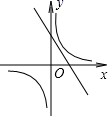 C.
C.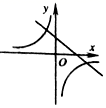 D.
D.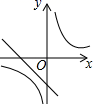
10.直线y=2x﹣6与x轴的交点坐标是( )
A.(0,3) B.(3,0) C.(0,﹣6) D.(﹣3,0)
二、填空题(本大题共有6小题,每小题3分,共18分)
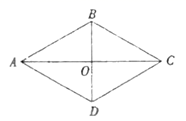
11.如图,菱形ABCD的周长是20,对角线AC、BD相交于点O.若BO=3,则菱形ABCD的面积为______.
12.直线![]() 与
与![]() 轴的交点坐标___________
轴的交点坐标___________
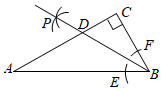
13.如图,在Rt![]() ACB中,∠C=90°,AB=2
ACB中,∠C=90°,AB=2![]() ,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于
,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于![]() EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则
EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则![]() ABD的面积为_____.
ABD的面积为_____.
14.换元法解方程![]() 时,可设
时,可设![]() ,那么原方程可化为关于
,那么原方程可化为关于![]() 的整式方程为_________.
的整式方程为_________.
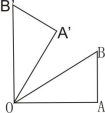
15.如图,∠A=90°,∠AOB=30°,AB=2,△![]() 可以看作由△AOB绕点O逆时针旋转60°得到的,则点
可以看作由△AOB绕点O逆时针旋转60°得到的,则点![]() 与点B的距离为_______.
与点B的距离为_______.
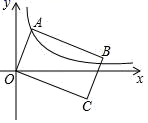
16.如图,已知点 A 是反比例函数 y ![]() 在第一象限图象上的一个动点,连接 OA,以
在第一象限图象上的一个动点,连接 OA,以![]() OA 为长,OA为宽作矩形 AOCB,且点 C 在第四象限,随着点 A 的运动,点 C 也随之运动,但点 C 始终在反比例函数 y
OA 为长,OA为宽作矩形 AOCB,且点 C 在第四象限,随着点 A 的运动,点 C 也随之运动,但点 C 始终在反比例函数 y ![]() 的图象上,则 k 的值为________.
的图象上,则 k 的值为________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线交AB于点D,交AC于点E.
求证:AE=2CE.
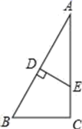
18.(8分)码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/元)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
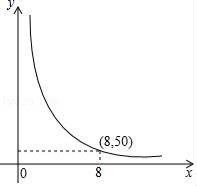
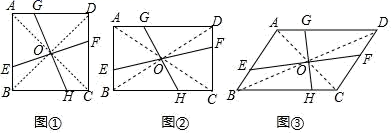
19.(8分)在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(1)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S四边形AEOG= S正方形 ABCD;
(2)如图②,若四边形 ABCD 是矩形,且 S四边形 AEOG=![]() S矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(3)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.
20.(8分)如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() .边
.边![]() 在其所在的直线上平移,将通过平移得到的线段记为
在其所在的直线上平移,将通过平移得到的线段记为![]() ,连接
,连接![]() 、
、![]() ,并过点
,并过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .
.
(1)请直接写出线段![]() 在平移过程中,四边形
在平移过程中,四边形![]() 是什么四边形;
是什么四边形;
(2)请判断![]() 、
、![]() 之间的数量关系和位置关系,并加以证明;
之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
21.(8分)某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆A,B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
A | 30人/辆 | 380元/辆 |
B | 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数设学校租用A型号客车x辆,租车总费用为y元.
(Ⅰ)求y与x的函数解析式,请直接写出x的取值范围;
(Ⅱ)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
22.(10分)往一个长25m,宽11m的长方体游泳池注水,水位每小时上升0.32m,
(1)写出游泳池水深d(m)与注水时间x(h)的函数表达式;
(2)如果x(h)共注水y(m3),求y与x的函数表达式;
(3)如果水深1.6m时即可开放使用,那么需往游泳池注水几小时?注水多少(单位:m3)?
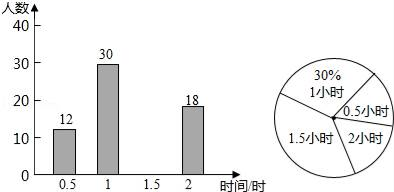
23.(10分)我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
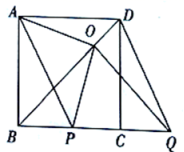
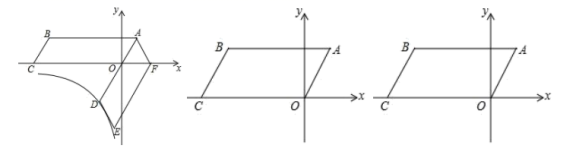
24.(12分)如图,在平面直角坐标系中,四边形![]() 为平行四边形,
为平行四边形,![]() 为坐标原点,
为坐标原点,![]() ,将平行四边形
,将平行四边形![]() 绕点
绕点![]() 逆时针旋转得到平行四边形
逆时针旋转得到平行四边形![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 落在
落在![]() 轴正半轴上.
轴正半轴上.
(1)证明:![]() 是等边三角形:
是等边三角形:
(2)平行四边形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() .
.![]() 的对应线段为
的对应线段为![]() ,点
,点![]() 的对应点为
的对应点为![]()
①直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标:
的坐标:
②对角线![]() 在旋转过程中设点
在旋转过程中设点![]() 坐标为
坐标为![]() ,当点
,当点![]() 到
到![]() 轴的距离大于或等于
轴的距离大于或等于![]() 时,求
时,求![]() 的范围.
的范围.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、D
4、B
5、C
6、B
7、B。
8、B
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、24
12、(0,-3)
13、![]()
14、![]()
15、1
16、−3![]()
三、解下列各题(本大题共8小题,共72分)
17、见解析
18、(1)![]() ;(2) 80吨货物;(3)6名.
;(2) 80吨货物;(3)6名.
19、(1)![]() ;(2)AG=
;(2)AG=![]() ;(3)当 AG=CH=
;(3)当 AG=CH=![]() ,BE=DF=1 时,直线 EF、GH 把四边形 ABCD 的面积四等分.
,BE=DF=1 时,直线 EF、GH 把四边形 ABCD 的面积四等分.
20、 (1)四边形![]() 是平行四边形;(2)
是平行四边形;(2)![]() 且
且![]() ,证明见解析;(3)见解析.
,证明见解析;(3)见解析.
21、 (1) 21≤x≤62且x为整数;(2)共有25种租车方案,当租用A型号客车21辆,B型号客车41辆时,租金最少,为19460元.
22、 (1)d=0.32x;(2)y=0.88x;(3)需往游泳池注水5小时;注水440m3
23、(1)详见解析;(2)144°;(3)众数为1.5小时、中位数为1.5小时.
24、(1)见解析(2)①P(0, ![]() )或(0, -4)②-8≤m≤-
)或(0, -4)②-8≤m≤-![]() 或
或![]() ≤m≤1
≤m≤1
广西壮族自治区南宁市第二中学2023-2024学年数学九年级第一学期期末学业水平测试试题含答案: 这是一份广西壮族自治区南宁市第二中学2023-2024学年数学九年级第一学期期末学业水平测试试题含答案,共8页。试卷主要包含了下列方程式属于一元二次方程的是等内容,欢迎下载使用。
2023-2024学年广西壮族自治区南宁市九上数学期末学业水平测试试题含答案: 这是一份2023-2024学年广西壮族自治区南宁市九上数学期末学业水平测试试题含答案,共7页。试卷主要包含了关于的一元二次方程的根的情况是,下列事件是必然事件的是等内容,欢迎下载使用。
重庆綦江区2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案: 这是一份重庆綦江区2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,正方形具有而菱形不具有的性质是,下列点在直线y=-x+1上的是,有下列说法,如果,那么下列各式正确的是等内容,欢迎下载使用。












