北京市2022-2023年上学期九年级期末数学试题知识点分类汇编-12垂径定理

这是一份北京市2022-2023年上学期九年级期末数学试题知识点分类汇编-12垂径定理，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

北京市2022-2023年上学期期末数学试题知识点分类汇编-12垂径定理

一、单选题
1．（2023秋·北京平谷·九年级统考期末）“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”这是《九章算术》中的一个问题，用现代的语言表述为：如图，为的直径，弦于E，寸，弦寸，则的半径为多少寸 （    ）

A．5 B．12 C．13 D．26

二、填空题
2．（2023秋·北京东城·九年级统考期末）《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积（弦×失+失²）．弧田（图中阴影部分）由圆弧和其所对的弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差．现有圆心角为，半径等于4米的弧田，按照上述公式计算出弧田的面积约为 米．（）

3．（2023秋·北京海淀·九年级期末）如图， 上有两点， 点在内， 若的半径为， 则弦的弦心距离 ， ．


三、解答题
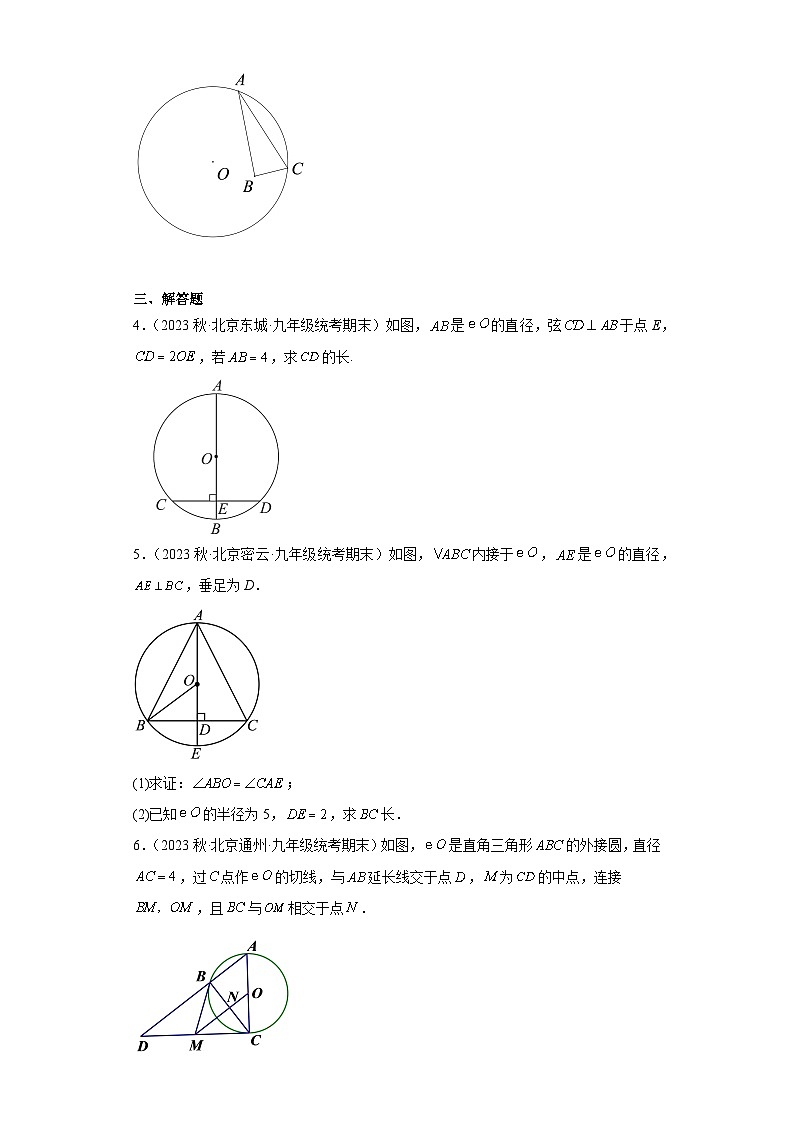
4．（2023秋·北京东城·九年级统考期末）如图，是的直径，弦于点E，，若，求的长.

5．（2023秋·北京密云·九年级统考期末）如图，内接于，是的直径，，垂足为D．

(1)求证：；
(2)已知的半径为5，，求长．
6．（2023秋·北京通州·九年级统考期末）如图，是直角三角形的外接圆，直径，过点作的切线，与延长线交于点，为的中点，连接，且与相交于点．

(1)求证：与相切；
(2)当时，在的圆上取点，使，求点到直线的距离．
7．（2023·北京海淀·九年级期末）紫砂壶是我国特有的手工制造陶土工艺品，其制作过程需要几十种不同的工具，其中有一种工具名为“带刻度嘴巴架”，其形状及使用方法如图1．当制显艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时，就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上．图2是正确使用该工具时的示意图．如图3，为某紫砂壶的壶口，已知，两点在上，直线过点，且于点，交于点．若，，求这个紫砂壶的壶口半径的长．

8．（2023·北京海淀·九年级期末）按要求作图：

(1)如图1，在正方形网格中，有一圆经过了两个小正方形的顶点A，B，利用无刻度直尺画出这个圆的一条直径；
(2)如图2，BA，BD是⊙O中的两条弦，C是BD上一点，ÐBAC=50°，利用无刻度直尺在图中画一个含有50°角的直角三角形；
(3)如图3，利用无刻度直尺和圆规，以AB边上一点O为圆心，过A、D两点作⊙O（不写作法，保留作图痕迹）；
(4)如图4，AB与圆相切，且切点为点B，利用无刻度直尺在网格中找出点B的位置．
9．（2023·北京海淀·九年级期末）如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过O作OH⊥AC于点H．若OH＝3，AB＝12，BO＝13，求：⊙O的半径和AC的长．

10．（2023秋·北京平谷·九年级统考期末）如图，已知劣弧，如何等分？下面给出两种作图方法，选择其中一种方法，利用直尺和圆规完成作图，并补全证明过程．

方法一：①作射线、；
②作的平分线，与交于点C；
点C即为所求作．
证明：∵平分，
∴
∴___（_____）（填推理的依据）．
方法二：①连接；
②作线段的垂直平分线，直线与交于点C；
点C即为所求作．
证明：∵垂直平分弦，
∴直线经过圆心O，
∴___（___）（填推理的依据）．
11．（2023·北京海淀·九年级期末）如图，有一座圆弧形拱桥，它的跨度为，拱高为．

(1)请用尺规作图，作出圆弧所在圆的圆心O，并计算圆的半径；
(2)当洪水泛滥到跨度只有时，就要采取紧急措施，若某次洪水中，水面离拱顶只有，即时，试通过计算说明是否需要采取紧急措施．
12．（2023·北京海淀·九年级期末）“五一”节期间，小明和同学一起到游乐场游玩．如图为某游乐场大型摩天轮的示意图，其半径是20m，它匀速旋转一周需要24分钟，最底部点B离地面1m．小明乘坐的车厢经过点B时开始计时．

(1)计时4分钟后小明离地面的高度是多少？
(2)在旋转一周的过程中，小明将有多长时间连续保持在离地面31m以上的空中？
13．（2023·北京海淀·九年级期末）圆管涵是公路路基排水中常用的涵洞结构类型，它不仅力学性能好，而且构造简单、施工方便．某水平放置的圆管涵圆柱形排水管道的截面是直径为的圆，如图所示，若水面宽，求水的最大深度．

14．（2023·北京海淀·九年级期末）蔬菜基地建圆弧形蔬菜大棚的剖面如图所示，已知，半径，求高度．

15．（2023·北京海淀·九年级期末）已知吃刀深度h为时，能在直径是d（）的轴上铣出宽的一块平面（如图）．

(1)求d的值．
(2)若吃刀深度增加到，求轴上铣出平面的宽度．
16．（2023·北京海淀·九年级期末）图1是某种型号圆形车载手机支架，由圆形钢轨、滑动杆、支撑杆组成．图2是它的正面示意图，滑动杆的两端都在圆O上，A、B两端可沿圆形钢轨滑动，支撑杆的底端C固定在圆O上，另一端D是滑动杆的中点，（即当支架水平放置时直线平行于水平线，支撑杆垂直于水平线），通过滑动A、B可以调节的高度．当经过圆心O时，它的宽度达到最大值，在支架水平放置的状态下：

(1)当滑动杆的宽度从10厘米向上升高调整到6厘米时，求此时支撑杆的高度．
(2)如图3，当某手机被支架锁住时，锁住高度与手机宽度恰好相等（），求该手机的宽度．

参考答案：
1．C
【分析】连接，构造直角三角形，根据垂径定理和勾股定理求解．
【详解】解：连接，如图所示，

设直径的长为，则半径，
为的直径，弦于，，
，
而，
根据勾股定理得，
解得，
即的半径为13寸．
故选C．
【点睛】此题考查了垂径定理和勾股定理；熟练掌握垂径定理，由勾股定理得出方程是解决问题的关键．
2．
【分析】由题意可知于D，交圆弧于C，由题意得米，解得米，再求出，最后由勾股定理得到，由垂径定理求出即可得出结果．
【详解】解：如图，由题意可知，

，，（米），
，
（米）
（米）
（米）
（米）
弧田面积


（平方米）
故答案为：
【点睛】本题考查了勾股定理以及垂径定理的应用；熟练掌握垂径定理是解答本题的关键．
3．
【分析】过点O作，垂足为D，根据垂径定理和勾股定理即可求出弦的弦心距离；延长交于点F，连接，，过点O作，垂足为点E，通过证明求出的长度，再结合垂径定理和勾股定理即可求出的长度．
【详解】解：过点O作，垂足为D，

在中，由勾股定理可得：，
∵，
∴，
∵半径为，
∴，
延长交于点F，连接，，过点O作，垂足为点E．

∵，
∴，
∵，
∴，
∵，，
∴，
∴，
∴，即，解得：，
∴，
∵，
∴，
∴，
在中，由勾股定理可得：，
∴在中，由勾股定理可得：，
故答案为：，．
【点睛】本题主要考查了垂径定理，勾股定理，解题的关键是熟练掌握相关知识点，根据题意作出辅助线求解．
4．.
【分析】由垂径定理得到，推出，在中，利用勾股定理即可求解.
【详解】解：如图，连接．

∵是的直径，弦于点E，
∴．
又∵，
∴．
∵，
∴．
在中，，
∴．
∴．
【点睛】本题考查了垂径定理、勾股定理，掌握垂直于弦的直径平分这条弦是解题的关键．
5．(1)见解析
(2)8

【分析】（1）由垂径定理可得，由圆周角定理得到，由得到，即可得到结论；
（2）由垂径定理可得，，在中，由勾股定理可得，即可得到长．
【详解】（1）证明：∵是的直径，，
∴，
∴，
∵，
∴是等腰三角形，
∴，
∴；
（2）∵是的直径，，
∴，，
在中，，，
∴，
∴．
【点睛】此题主要考查了垂径定理、圆周角定理、勾股定理等知识，熟练掌握垂径定理和圆周角定理的内容是解题的关键．
6．(1)见解析
(2)或

【分析】（1）根据题意可得，根据直径所对的圆周角是直角，得出，进而得出，证明，得出，即可得证；
（2）分点在以及半圆上，分别作出图形，根据含30度角的直角三角形的性质，勾股定理即可求解．
【详解】（1）证明：如图，

为的中点，是中点，
，
是的直径，
，
，
，
又，
，
，
是切线
，
，
，
是切线；
（2）当点在上时，连接，交于点，

，
，
，
，
直径，
，

，
当点在半圆上时，过点作，垂足为点,，垂足为点，

四边形是矩形，
在中，
，
，
，
．
【点睛】本题考查了切线的判定，全等三角形的性质与判定，垂径定理，直径所对的圆周角是直角，综合运用以上知识是解题的关键．
7．
【分析】连接，根据垂径定理求得，又由，即可由勾股定理求解．
【详解】解：如图，连接．

∵过圆心，，，
∴．
∵，
∴．
∵，
∴．
解得．
∴这个紫砂壶的壶口半径的长为．
【点睛】本题考查垂径定理，勾股定理，熟练掌握垂径定理是解题的关键．
8．(1)见解析；
(2)见解析；
(3)见解析；
(4)见解析．

【分析】（1）根据垂径定理可知，AB 的垂直平分线过圆心，连接AB，利用网格找出线段AB的垂直平分线即可；
（2）延长AC交⊙O与点E，连接BO并延长交⊙O于点F，在连接EF，则即为所求；
（3）作线段AD的垂直平分线，交AB于点O，再以点O为圆心，OA为半径作圆即可；
（4）过点A作圆的两条割线：ACD和AEF；连接CF，DE交于点G，延长EC和FD交于点H，连接HG交圆于点B，连接AB即可．
【详解】（1）解：根据垂径定理可知，AB 的垂直平分线过圆心，连接AB，利用网格找出线段AB的垂直平分线即可，如图：EF即为直径；

（2）解：延长AC交⊙O与点E，连接BO并延长交⊙O于点F，在连接EF，则即为所求；

（3）解：作线段AD的垂直平分线，交AB于点O，再以点O为圆心，OA为半径作圆即可，如图；

（4）解：过点A作圆的两条割线：ACD和AEF；连接CF，DE交于点G，延长EC和FD交于点H，连接HG交圆于点B，连接AB即可，如图：

【点睛】本题考查作图，圆周角定理，切线性质，垂直平分线，解题的关键是理解题意，综合运用所学知识，是中考中常见题型．
9．⊙O的半径为5，AC的长为8
【分析】利用切线的性质得∠OAB＝90°，则根据勾股定理可计算出OA＝5，再根据垂径定理得到AH＝CH，接着利用勾股定理计算出AH，从而得到AC的长．
【详解】解：∵AB为切线，
∴OA⊥AB，
∴∠OAB＝90°，
在中，OA＝＝＝5，
∵OH⊥AC，
∴AH＝CH，
在中，AH＝＝＝4，
∴AC＝2AH＝8，
答：⊙O的半径为5，AC的长为8．
【点睛】本题考查切线的性质，垂径定理，勾股定理，掌握利用垂径定理与勾股定理结合，求线段长是解题的关键．
10．方法一：画图见解析，，，在同圆或等圆中，相等的圆心角所对的弧相等；方法二：画图见解析，，，垂径定理．
【分析】方法一：按照作图语句提示作图，再根据圆心角与弧的关系进行证明即可；
方法二：按照作图语句提示作图，再根据垂径定理进行证明即可；
【详解】解：方法一：如图，点C即为所求作．

证明：∵平分，
∴
∴（在同圆或等圆中，相等的圆心角所对的弧相等）．
方法二：如图，点C即为所求作．

证明：∵垂直平分弦，
∴直线经过圆心O，
∴（垂径定理）．
【点睛】本题考查的是复杂的作图，平分弧的作图，熟练的利用基本作图解决复杂的作图是解本题的关键，同时考查了角平分线的定义，线段的垂直平分线的性质．
11．(1)拱桥所在的圆的半径
(2)不需要采取紧急措施，理由见解析

【分析】（1）连接，作的垂直平分线，延长与的垂直平分线相交于点O，点O即为所求的圆弧所在圆的圆心，连接，由垂径定理可知，再在中，由勾股定理得出方程，即可求出半径；
（2）求出，再由勾股定理可得，则，即可得出结论．
【详解】（1）如图，点O即为所求的圆弧所在圆的圆心，连接，

设半径为，则，
由垂径定理可知，
∵，
∴，
在中，，
由勾股定理可得，，
即，
解得，
∴拱桥所在的圆的半径；
（2）∵，
∴
在中，由勾股定理可得，
，
∴，
∴不需要采取紧急措施．
【点睛】本题考查了作图—垂直平分线、垂径定理和勾股定理的应用，灵活运用所学知识求解是解决本题的关键．
12．(1)计时4分钟后小明离地面的高度是11m
(2)8分钟

【分析】（1）设4分钟后小明到达点，过点作    于点，先算出的度数，再根据三角函数计算出的长度，即可算出的长度.
（2）假设距离地面31米，先算出长度，再根据三角函数值算出的度数，进而可知的度数，即可算出小明将连续保持在离地面31m以上的空中的时间.
【详解】（1）解：设4分钟后小明到达点，过点作于点，即为小明离地的高度，
∵
∴
(m)．
答：计时4分钟后小明离地面的高度是11m；
（2）解：∵当旋转到处时，作弦交的延长线于点，连接，此时离地面高度为．
当时，
，



∵每分钟旋转的角度为： ，    
∴由点旋转到所用的时间为：（分钟）．
答：在旋转一周的过程中，小明将有8分钟的时间连续保持在离地面31m以上的空中．

【点睛】本题主要考查了垂径定理，熟练掌握垂径定理是解题的关键.
13．0.8m
【分析】过点作于点，连接，根据垂径定理得到，再在中，根据勾股定理可求出，进而即可求解．
【详解】解：如图，作于点，连接，

∵，，
∵，
∴，
在中，根据勾股定理，得，
∴，
∴水的最大深度为0.8m．
【点睛】此题主要考查了垂径定理的应用，以及勾股定理，熟练掌握定理是解题的关键．
14．
【分析】弦，半径，根据题意得是直角三角形，可求出的长，由此即可求解．
【详解】解：根据题意得，在中，，半径，
∴，，，
∴，
故答案是：．
【点睛】本题主要考查垂径定理、勾股定理，掌握垂径定理是解题的关键．
15．(1)
(2)

【分析】（1）设圆心为O，过点O作于点C，的延长线交于点D，连接，在中，利用勾股定理列出方程求出半径，即可解答；
（2）在中，利用勾股定理先求出，即可求出．
【详解】（1）设圆心为O，过点O作于点C，的延长线交于点D，连接，如图，

∵，，
∴，
∵，
设，
∴，
在中，根据勾股定理得，，
即，
解得，
∴直径，
即直径d的值为；
（2）根据（1）中的结果有：，
当时，则，
∵ ，
∴ ，
根据勾股定理得，，
即，
解得，
∴，
∴轴上铣出平面的宽度为．
【点睛】本题考查了垂径定理的应用，解题的关键是添加辅助线构造直角三角形利用勾股定理解决问题．
16．(1)支撑杆的高度为9cm．
(2)手机的宽度为8cm．

【分析】（1）如图，连结OA，由题意可得：的直径为10， 由 先求解 从而可得答案；
（2）如图，记圆心为O，连结OA，证明 设则则 再利用勾股定理建立方程求解即可．
【详解】（1）解：如图，连结OA，由题意可得：的直径为10，

即




所以此时支撑杆的高度为9cm．
（2）解：如图，记圆心为O，连结OA，

由题意可得：
∴四边形为正方形，



设
则


由勾股定理可得：
解得
经检验不符合题意，舍去，取
（cm），
即手机的宽度为8cm．
【点睛】本题考查的是正方形的判定与性质，垂径定理的应用，勾股定理的应用，一元二次方程的解法，理解题意，建立方程解题是关键．