




专题23.1 旋转(基础)-【题型分层练】2022-2023学年九年级数学上册单元题型精练(基础题型+强化题型)(人教版)
展开TOC \ "1-3" \h \z \u \l "_Tc116602161" 求旋转角 PAGEREF _Tc116602161 \h 1
\l "_Tc116602162" 求长度 PAGEREF _Tc116602162 \h 2
\l "_Tc116602163" 求相关角度 PAGEREF _Tc116602163 \h 3
\l "_Tc116602164" 综合运用 PAGEREF _Tc116602164 \h 4
\l "_Tc116602165" 求最值 PAGEREF _Tc116602165 \h 5
\l "_Tc116602166" 旋转的变化过程 PAGEREF _Tc116602166 \h 6
\l "_Tc116602167" 确定旋转中心 PAGEREF _Tc116602167 \h 6
\l "_Tc116602168" 判断中心对称图形 PAGEREF _Tc116602168 \h 8
\l "_Tc116602169" 中心对称与坐标 PAGEREF _Tc116602169 \h 9
\l "_Tc116602170" 作图题 PAGEREF _Tc116602170 \h 9
\l "_Tc116602171" 网格中的作图题 PAGEREF _Tc116602171 \h 10
\l "_Tc116602172" 综合运用 PAGEREF _Tc116602172 \h 11
求旋转角
在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。
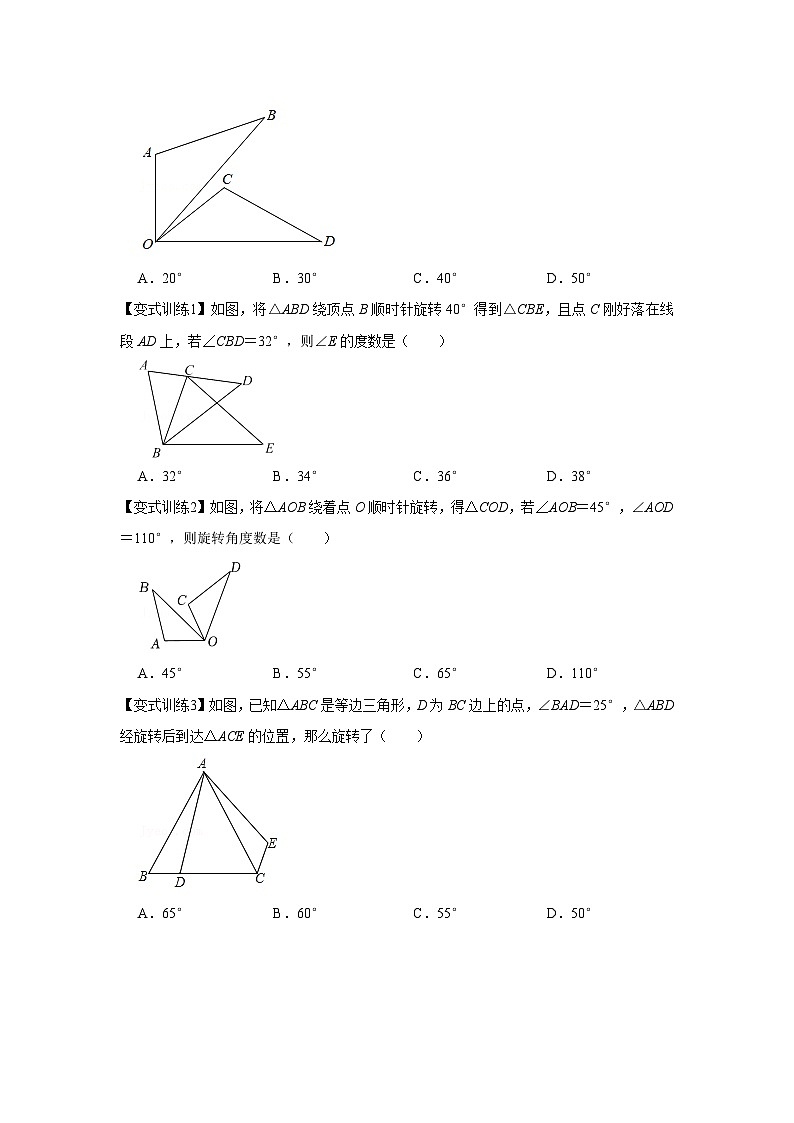
如图,将△AOB绕着点O顺时针旋转,得到△COD(点C落在△AOB外),若∠AOB=30°,∠BOC=10°,则旋转角度是( )
A.20°B.30°C.40°D.50°
如图,将△ABD绕顶点B顺时针旋转40°得到△CBE,且点C刚好落在线段AD上,若∠CBD=32°,则∠E的度数是( )
A.32°B.34°C.36°D.38°
如图,将△AOB绕着点O顺时针旋转,得△COD,若∠AOB=45°,∠AOD=110°,则旋转角度数是( )
A.45°B.55°C.65°D.110°
如图,已知△ABC是等边三角形,D为BC边上的点,∠BAD=25°,△ABD经旋转后到达△ACE的位置,那么旋转了( )
A.65°B.60°C.55°D.50°
求长度
对应点到旋转中心的距离相等,对应点到旋转中心所连线段的夹角等于旋转角,旋转前后的两个图形全等。
如图,在Rt△ABC中,∠B=90°,BC=5,AB=12,将△ABC绕点A顺时针旋转90°得到△AB'C',连接CC',则CC'的长为( )
A.13B.132C.213D.26
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点B逆时针旋转得△A′BC',若点C′在AB上,则AA′的长为( )
A.13B.4C.25D.5
如图,在△AOB中,AO=1,BO=AB=32.将△AOB绕点O逆时针方向旋转90°,得到△A'OB',连接AA',BB',则BB'﹣AA'=( )
A.1B.22C.32D.322
如图,将△ABC绕点A顺时针旋转60°得到△AED,若AB=3cm,则BE等于( )
A.2cmB.3cmC.4cmD.5cm
求相关角度
如图,将△ABC绕点A逆时针旋转80°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小是( )
A.45°B.50°C.60°D.100°
如图,将△ABC绕顶点C顺时针旋转35°得到△DEC,点A、B的对应点分别是点D和点E.设边ED,AC相交于点F.若∠A=30°,则∠EFC的度数为( )
A.60°B.65°C.72.5°D.115°
如图,将△ABC绕着点A逆时针旋转65°,得到△AED,若∠E=35°,AD∥BC,则∠EAC的度数为( )
A.35°B.25°C.15°D.5°
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB'C',若点B'在线段BC的延长线上,则∠BB'C'的度数为( )
A.60°B.70°C.80°D.100°
综合运用
如图,O是等边△ABC内一点,OA=3,0B=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:
①△BO'A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④S四边形AOBO′=6+33;
⑤S△AOC+﹣S△AOB=6+3.
其中结论正确的是( )
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
如图,点D为等边三角形ABC内的一点,DA=10,DB=8,DC=6,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为10;②△ACD'绕点A顺时针旋转60°会和△ABD重合;③CD⊥CD';④S四边形ADCD′=24+253,其中正确的有( )
A.1个B.2个C.3个D.4个
求最值
如图,在三角形ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边三角形PBC,则AP的最大值是 .
如图,△ABC是等边三角形,且AB=4,点D在边BC上,连接AD,将线段AD绕点A顺时针旋转60°,得到线段AE,连接DE,BE.则△BED的周长最小值是 .
旋转的变化过程
有一个正n边形旋转90°后与自身重合,则n为( )
A.6B.9C.12D.15
如图,五角星的五个顶点等分圆周,把这个图形绕着圆心顺时针旋转一定的角度后能与自身重合,那么这个角度至少为( )
A.60°B.72°C.75°D.90°
下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,逆时针旋转∠α,要使这个∠α最小时,旋转后的图形也能与原图形完全重合,则这个图形是( )
A.B.C.D.
一个正三角形绕其中心至少旋转 度,才能与自身重合.
确定旋转中心
旋转中心是两对对应点所连线段的垂直平分线的交点
如图,在正方形网格中,点A的坐标为(0,5),点B的坐标为(4,3),线段AB绕着某点旋转一个角度与线段CD重合(C、D均为格点),若点A的对应点是点C,则它的旋转中心的坐标是( )
A.(1,2)B.(2,1)C.(3,1)D.(5,4)
如图,在正方形网格中,△EFG绕某一点旋转某一角度得到△RPQ.则旋转中心可能是( )
A.点AB.点BC.点CD.点D
如图,若正方形ABCD绕图中某点逆时针旋转90°得到正方形EFGH,则旋转中心应是( )
A.H点B.N点C.C点D.M点
如图,在6×6的正方形网格中,△ABC绕某点旋转一定的角度,得到△ABC,则旋转中心是点( )
A.OB.PC.QD.M
判断中心对称图形
如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形。中心对称:如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称。
下列图形中,是轴对称图形,但不是中心对称图形的是( )
A.B.
C.D.
民族图案是数学文化中的一块瑰宝.下列图案中,是轴对称图形但不是中心对称图形的是( )
A.B.
C.D.
下列图形中,是中心对称图形也是轴对称图形的是( )
A.B.C.D.
下列图形既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
中心对称与坐标
点P(x,y)关于原点对称点的坐标是(-x,-y)
若P(x,3)与点Q(4,y)关于原点对称,则xy的值是( )
A.12B.﹣12C.64D.﹣64
故选:A.
已知点P(m﹣3,m﹣1)关于原点的对称点P′在第四象限,则m的取值范围在数轴上表示正确的是( )
A.B.
C.D.
已知点A(a+b,4)与点B(﹣2,a﹣b)关于原点对称,则a与b的值分别为( )
A.﹣3;1B.﹣1;3C.1;﹣3D.3;﹣1
已知点M(a,b)在第二象限内,且|a|=1,|b|=2,则该点关于原点对称点的坐标是( )
A.(﹣2,1)B.(﹣1,2)C.(2,﹣1)D.(1,﹣2)
作图题
在4×4的方格中,选择6个小方格涂上阴影,请仔细观察图1中的六个图案的对称性,按要求回答.
(1)请在六个图案中,选出三个具有相同对称性的图案.
选出的三个图案是 (填写序号);
它们都是 图形(填写“中心对称”或“轴对称”);
(2)请在图2中,将1个小方格涂上阴影,使整个4×4的方格也具有(1)中所选图案相同的对称性.
如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
网格中的作图题
如图,在平面直角坐标系中,已知点A(2,﹣2),点P是x轴上的一个动点.
(1)A1,A2分别是点A关于原点的对称点和关于y轴对称的点,直接写出点A1,A2的坐标,并在图中描出点A1,A
(2)求使△APO为等腰三角形的点P的坐标.
如图,在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,﹣2),B(4,﹣1),C(3,﹣3)(正方形网格中,每个小正方形的边长都是1个单位长度).
(1)若△A1B1C1与△ABC关于原点O成中心对称,则点A1的坐标为 ;
(2)以坐标原点O为旋转中心,将△ABC逆时针旋转90°,得到△A2B2C2,则点A2的坐标为 ;
(3)求出(2)中线段AC扫过的面积.
综合运用
如图,在△ABC中,AB=AC=5,BC=6,AO⊥BC于点O,在△ABC的外部以AB为边作等边△ABD,点E是线段AO上一动点(点E不与点A重合),将线段BE绕点B顺时针方向旋转60°得到线段BF.
(1)若BF=23,求证:C,E,F三点共线;
(2)连结DF,若△BDF的面积为3,求BF的长.
如图,等腰△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A逆时针旋转一定角度α(45°<α≤90°)得到△ADE,点B、C的对应点分别是D、E.连结BD、CE交于点F,连结AD、CE交于点G.
(1)用含α的代数式表示∠AGC的度数;
(2)当AE∥BD时,求CF的长.
如图,在矩形ABCD中,点E在边BC上,将线段AE绕点E顺时针旋转90°,此时点A落在点F处,线段EF交CD于点M.过点F作FG⊥BC,交BC的延长线于点G.
(1)求证:BE=FG;
(2)如果AB⋅DM=EC⋅AE,联结AM、DE,求证:AM垂直平分DE.
如图,矩形ABCD绕B点旋转,使C点落到AD上的E处,AB=AE,连接AF,AG.
(1)求证:AF=AG;
(2)求∠GAF的度数.
一.选择题(共8小题)
1.小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形从当前位置开始进行一次平移操作,平移后的正方形的顶点仍在图中格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有
A.3个B.4个C.5个D.6个
2.观察下列图案,其中旋转角最大的是
A.B.C.D.
3.下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是
A.B.
C.D.
4.如图,中,,将绕点旋转,得到,点的对应点在的延长线上,则旋转方向和旋转角可能为
A.逆时针,B.逆时针,C.顺时针,D.顺时针,
5.如图所示的正六边形花环绕中必至少旋转度能与自身重合,则为
A.30B.60C.120D.180
6.如图,的顶点坐标、、,若绕点按逆时针方向旋转,再向右平移2个单位,得到△,则点的对应点的坐标是
A.B.C.D.
7.如图,点为矩形的两对角线交点,动点从点出发沿边向点运动,同时动点从点出发以相同的速度沿边向点运动,作直线,下列说法错误的是
A.直线平分矩形的周长
B.直线必平分矩形的面积
C.直线必过点
D.直线不能将矩形分成两个正方形
8.最近北京2022年冬奥会的吉祥物“冰墩墩”成为了互联网的“顶流”,他呆萌的形象受到了人们的青睐,结合你所学知识,从下列四个选项中选出能够和如图的图片成中心对称的是
A.B.C.D.
二.填空题(共4小题)
9.如图是的正方形网格,要在图中再涂黑一个小正方形,使得图中黑色的部分成为轴对称图形,这样的小正方形有 个.
10.如图,一个小孩坐在秋千上,秋千绕点旋转了,小孩的位置也从点运动到了点,则 度.
11.小明对小亮说:“你将这4张扑克牌任意抽取一张,将其旋转后放回原处,我能猜出你旋转的那一张”,小亮在小明不看的情况下,抽取一张旋转后放回原处.小明很快猜出了被旋转的那张扑克牌.
小亮旋转的那张扑克牌的牌面数字是 .
12.如图,点为定角的平分线上的一个定点,且与互补,若在绕点旋转的过程中,其两边分别与、相交于点、,则以下结论:①恒成立;②的值不变;③的周长不变;④四边形的面积不变,其中正确的序号为 .
三.解答题(共3小题)
13.在的网格中已经涂黑了三个小正方形,请在图中涂黑一块(或两块)小正方形,使涂黑的四个(或五个)小正方形组成一个轴对称图形.
14.如图,矩形中,,将矩形绕点顺时针旋转得到矩形.当点恰好落在边上时,旋转角为,连接.若,求旋转角及的长.
15.(1)计算:;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 个;第2008个图案是 .
专题23.1 旋转中的最值问题(强化)-【题型分层练】2022-2023学年九年级数学上册单元题型精练(基础题型+强化题型)(人教版): 这是一份专题23.1 旋转中的最值问题(强化)-【题型分层练】2022-2023学年九年级数学上册单元题型精练(基础题型+强化题型)(人教版),文件包含九年级数学上册专题231旋转中的最值问题强化原卷版docx、九年级数学上册专题231旋转中的最值问题强化解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
专题24.4 弧长和扇形面积(基础)-【题型分层练】2022-2023学年九年级数学上册单元题型精练(基础题型+强化题型)(人教版): 这是一份专题24.4 弧长和扇形面积(基础)-【题型分层练】2022-2023学年九年级数学上册单元题型精练(基础题型+强化题型)(人教版),文件包含九年级数学上册专题244弧长和扇形面积基础原卷版docx、九年级数学上册专题244弧长和扇形面积基础解析版docx等2份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。
专题24.3 圆的证明综合(强化)-【题型分层练】2022-2023学年九年级数学上册单元题型精练(基础题型+强化题型)(人教版): 这是一份专题24.3 圆的证明综合(强化)-【题型分层练】2022-2023学年九年级数学上册单元题型精练(基础题型+强化题型)(人教版),文件包含九年级数学上册专题243圆的证明综合强化原卷版docx、九年级数学上册专题243圆的证明综合强化解析版docx等2份试卷配套教学资源,其中试卷共59页, 欢迎下载使用。












