第26章概率初步测试题（沪科版九下）
展开概率初步测试题
（说明：全卷考试时间100分钟，满分120分）
一、选择题（每小题3分，共30分）
1. 下列事件中是必然事件的是（ ）
A．小菊上学一定乘坐公共汽车
B．某种彩票中奖率为
，买10000张该种票一定会中奖
C．一年中，大、小月份数刚好一样多
D．将豆油滴入水中，豆油会浮在水面上
2．从A地到C地，可供选择的方案是走水路、走陆路、走空中.从A地到B地有2条水路、2.条陆路，从B地到C地有3条陆路可供选择，走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有（ ）
A．20种 B.8种 C. 5种 D.13种
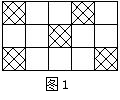
3．一只小狗在如图1的方砖上走来走去，最终停在阴
影方砖上的概率是（ ）
A．
B.
C.
D.
4．下列事件发生的概率为0的是（ ）
A．随意掷一枚均匀的硬币两次，至少有一次反面朝上；
B．今年冬天黑龙江会下雪；
C．随意掷两个均匀的骰子，朝上面的点数之和为1；
D．一个转盘被分成6个扇形，按红、白、白、红、红、白排列，转动转盘，指针停在红色区域。
5.某商店举办有奖储蓄活动，购货满100元者发对奖券一张，在10000张奖券中，设特等奖1个，一等奖10个，二等奖100个。若某人购物满100元，那么他中一等奖的概率是 （ ）
A. 
B. 
C. 
D. 
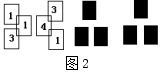6、有6张写有数字的卡片，它们的背面都相同，现将它们背面朝上（如图2），从中任意一张是数字3的概率是（ ）
A.
B. C.
D.
7.在李咏主持的“幸运52”栏目中，曾有一种竞猜游戏，游戏规则是：在20个商标牌中，有5个商标牌的背面注明了一定的奖金，其余商标牌的背面是一张“哭脸”，若翻到“哭脸”就不获奖,参与这个游戏的观众有三次翻牌的机会，且翻过的牌不能再翻．有一位观众已翻牌两次，一次获奖，一次不获奖，那么这位观众第三次翻牌获奖的概率是（ ）
A．
B．
C．
D．
8.如图3,一飞镖游戏板,其中每个小正方形的大小相等,则随意投掷一个飞镖,击中黑色区域的概率是 ( )
A. B. 
C. 
D.
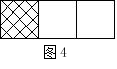
9.如图4，一小鸟受伤后，落在阴影部分的概率为（ ）
A． B． C． D．1
10.连掷两次骰子，它们的点数都是4的概率是（ ）
A. B. C.
D.
二、填空题（每小题3分，共30分）
11. （08福建福州）在一个袋子中装有除颜色外其它均相同的2个红球和3个白球，从中任意摸出一个球，则摸到红球的概率是____________
12.小明、小刚、小亮三人正在做游戏，现在要从他们三人中选出一人去帮王奶奶干活，则小明被选中的概率为______,小明未被选中的概率为______
13.在一次抽奖活动中，中奖概率是0.12，则不中奖的概率是 ．
14.从一副扑克牌（除去大、小王）中任抽一张，则抽到红心的概率为 ；抽到黑桃的概率为 ；抽到红心3的概率为
15.任意翻一下2007年日历，翻出1月6日的概率为 ;翻出4月31日的概率为 。
16.单项选择题是数学试题的重要组成部分，当你遇到不会做的题目时，如果你随便选一个答案（假设每个题目有4个选项），那么你答对的概率为 。
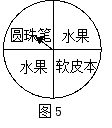
17.某班的联欢会上，设有一个摇奖节目，奖品为圆珠笔、软皮本和水果，
标在一个转盘的相应区域上（转盘被均匀等分为四个区域，如图5）。转盘可以自由转动。参与者转动转盘，当转盘停止时，指针落在哪
一区域，就获得哪种奖品，则获得圆珠笔的概率为 。
18.一位汽车司机准备去商场购物，然后他随意把汽车停在某个停车场内，如图6,停车场分A、B两区，停车场内一个停车位置正好占一个方格且一个方格除颜色外完全一样，则汽车停在A区蓝色区域的概率是 ，停在B区蓝色区域的概率是
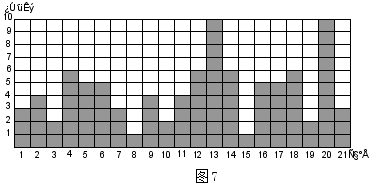
19.如图7表示某班21位同学衣服上口袋的数目。若任选一位同学，则其衣服上口袋数目为5的概率是 .
20.一个小妹妹将10盒蔬菜的标签全部撕掉了。现在每个盒子看上去都一样,但是她知道有三盒玉米、两盒菠菜、四盒豆角、一盒土豆。她随机地拿出一盒并打开它。则盒子里面是玉米的概率是 ，盒子里面不是菠菜的概率是 。
三、解答题（共60分）
21. （6分）将下面事件的字母写在最能代表它的概率的点上。
A．投掷一枚硬币时，得到一个正面。
B．在一小时内，你步行可以走80千米。
C．给你一个骰子中，你掷出一个3。
D．明天太阳会升起来。
22. （6分）一个桶里有60个弹珠——一些是红色的，一些是蓝色的，一些是白色的。拿出红色弹珠的概率是35%，拿出蓝色弹珠的概率是25%。桶里每种颜色的弹珠各有多少？
23. （8分）23、在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复。下表是活动进行中的一组统计数据：
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
（1）请估计：当n很大时，摸到白球的频率将会接近 ；
（2）假如你去摸一次，你摸到白球的概率是 ，摸到黑球的概率是 ；
（3）试估算口袋中黑、白两种颜色的球各有多少只?
24. （8分）小猫在如图9所示的地板上自由地走来走去，它最终停留在红色方砖上的概率是，你试着把每块砖的颜色涂上。
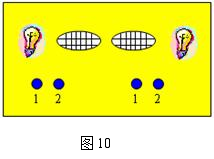
25. （10分）如图10依据闯关游戏规则，请你探究“闯关游戏”的奥秘：
（1）用列表的方法表示有可能的闯关情况；
（2）求出闯关成功的概率.
26.（10分）某同学抛掷两枚硬币，分10级实验，每组20次，下面是共计200次实验中记录下的结果.
实验组别 | 两个正面 | 一个正面 | 没有正面 |
第1组 | 6 | 11 | 3 |
第2组 | 2 | 10 | 8 |
第3组 | 6 | 12 | 2 |
第4组 | 7 | 10 | 3 |
第5组 | 6 | 10 | 4 |
第6组 | 7 | 12 | 1 |
第7组 | 9 | 10 | 1 |
第8组 | 5 | 6 | 9 |
第9组 | 1 | 9 | 10 |
第10组 | 4 | 14 | 2 |
①在他的每次实验中，抛出_____、_____和_____都是随机事件.
②在他的10组实验中，抛出“两个正面”概率最多的是他第_____组实验，抛出“两个正面”概率最少的是他的第_____组实验.
③在他的第1组实验中抛出“两个正面”的概率是_____，在他的前两组(第1组和第2组)实验中抛出“两个正面”的概率是_____.
④在他的10组实验中，抛出“两个正面”的概率是_____，抛出“一个正面”的概率是_____，“没有正面”的概率是_____，这三个概率之和是_____.
27. （12分）（08茂名）透明的口袋里装有3个球，这3个球分别标有数字1、2、3，这些球除了数字以外都相同．
（1）如果从袋中任意摸出一个球，那么摸到标有数字是2的球的概率是多少？（2分）
（2）小明和小东玩摸球游戏，游戏规则如下：先由小明随机摸出一个球，记下球的数字后放回，搅匀后再由小东随机摸出一个球，记下球的数字．谁摸出的球的数字大，谁获胜．现请你利用树状图或列表的方法分析游戏规则对双方是否公平？并说明理由．（6分）
一、1．B 2．D 3．B 4．C 5．B 6．B 7．B 8．B 9．B 10．D
二、11．
12． 13．0.88 14． 
15． 
0 16． 17． 18． 
19．
20．
三、21．A．； B．0；C．；D．1
22．解：显然拿出白色弹珠的概率是40%，
红色弹珠有60×25%=15，
蓝色弹珠有60×35%=21，
白色弹珠有60×40%=24。
23．解：（1）0.6；（2）0.6；0.4；（3）黑8、白12。
24．
25．解：（1）所有可能的闯关情况列表表示如下表：
右边按钮 左边按钮 | 1 | 2 |
1 | （1，1） | （1，2） |
2 | （2，1） | （2，2） |
（2）设两个1号按钮各控制一个灯泡P（闯关成功）= 。
26．解：①“两个正面”“一个正面”“没有正面”；
②7 9；
③ ；
④
1。
27.解：参考答案】
（1）从3个球中随机摸出一个，摸到标有数字是2的球的概率是
或P（摸到标有数字是2的球）=
（2）游戏规则对双方公平．
树状图法： 或列表法：
| 1 | 2 | 3 |
1 | （1，1） | （1，2） | （1，3） |
2 | （2，1） | （2，2） | （2，3） |
3 | （3，1） | （3，2） | （3，3） |
1 （1，1）
1 2 （1，2）
3 （1，3）
1 （2，1）
开始 2 2 （2，2）
3 （2，3）
1 （3，1）
3 2 （3，2）
3 （3，3）
