广东省广州海珠区四校联考2022-2023学年数学七下期末调研试题含答案

广东省广州海珠区四校联考2022-2023学年数学七下期末调研试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

请考生注意：

1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题(每小题3分,共30分)

1．如图，EF是Rt△ABC的中位线，∠BAC＝90°，AD是斜边BC边上的中线，EF和AD相交于点O，则下列结论不正确的是（　　）

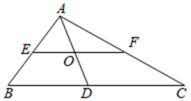
A．AO＝OD B．EF＝AD C．S△AEO＝S△AOF D．S△ABC＝2S△AEF

2．如图，△ABC是等边三角形，点P是三角形内的任意一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为12，则PD+PE+PF＝(　　)

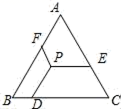
A．12 B．8 C．4 D．3

3．如图，等边三角形的边长为4，点是△ABC的中心，，的两边与分别相交于，绕点顺时针旋转时，下列四个结论正确的个数是（   ）

①；②；③；④周长最小值是9.

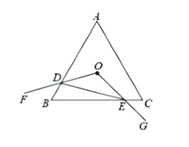
A．1个 B．2个 C．3个 D．4个

4．如图，已知两直线l1：y＝x和l2：y＝kx﹣5相交于点A(m，3)，则不等式x≥kx﹣5的解集为(　　)

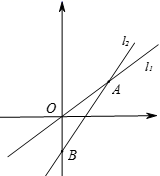
A．x≥6 B．x≤6 C．x≥3 D．x≤3

5．一个多边形的内角和比其外角和的2倍多180°，那么这个多边形是（  ）

A．五边形 B．六边形 C．七边形 D．八边形

6．如图，函数y＝mx+n和y＝﹣2x的图象交于点A（a，4），则方程mx+n＝﹣2x的解是（　　）

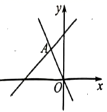
A．x＝﹣2 B．x＝﹣3 C．x＝﹣4 D．不确定

7．下列式子为最简二次根式的是（）

A． B． C． D．

8．如图，在中，，，平分交于点，点为的中点，连接，则的周长为（    ）

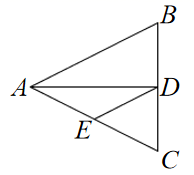
A．12 B．14 C．15 D．20

9．函数y＝﹣x﹣3的图象不经过（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

10．如图，四边形ABCD中，AB＝CD，对角线AC，BD交于点O，下列条件中不能说明四边形ABCD是平行四边形的是(　　)

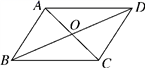
A．AD＝BC B．AC＝BD

C．AB∥CD D．∠BAC＝∠DCA

二、填空题(本大题共有6小题，每小题3分，共18分)

11．某县为了节约用水，自建了一座污水净化站，今年一月份净化污水3万吨，三月份增加到3.63万吨，则这两个月净化的污水量每月平均增长的百分率为______．

12．如图，在中，，，，则__________.

13．已知：正方形ABCD的边长为8，点E、F分别在AD、CD上，AE＝DF＝2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为_____．

14．命题“全等三角形的对应角相等”的逆命题是____________________________这个逆命题是______(填“真”或“假”)

15．在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感.按此比例，如果雕像的高度为 1m，那么它的下部应设计的高度为_____．

16．如果关于的不等式组的整数解仅有,,那么适合这个不等式组的整数,组成的有序数对共有_______个；如果关于的不等式组(其中,为正整数)的整数解仅有,那么适合这个不等式组的整数,组成的有序数对共有______个.(请用含、的代数式表示)

三、解下列各题(本大题共8小题，共72分)

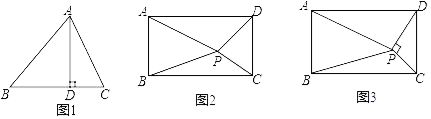
17．（8分）（几何背景）如图1，AD为锐角△ABC的高，垂足为D．求证：AB2﹣AC2＝BD2﹣CD2

（知识迁移）如图2，矩形ABCD内任意一点P，连接PA、PB、PC、PD，请写出PA、PB、PC、PD之间的数量关系，并说明理由．

（拓展应用）如图3，矩形ABCD内一点P，PC⊥PD，若PA＝a，PB＝b，AB＝c，且a、b、c满足a2﹣b2＝c2，则的值为　   　（请直接写出结果）

18．（8分）解方程：

（1）

（2）2x2﹣2x﹣1＝0

19．（8分）（1）如图1，观察函数y=|x|的图象，写出它的两条的性质；

（2）在图1中，画出函数y=|x-3|的图象；

根据图象判断：函数y=|x-3|的图象可以由y=|x|的图象向          平移          个单位得到；

（3）①函数y=|2x+3|的图象可以由y=|2x|的图象向      平移           单位得到；

②根据从特殊到一般的研究方法，函数y=|kx+3|（k为常数，k≠0）的图象可以由函数y=|kx|（k为常数，k≠0）的图象经过怎样的平移得到．

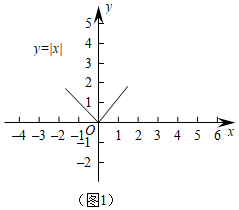
20．（8分）如图，在四边形AOBC中，AC∥OB，顶点O是原点，顶点A的坐标为（0，8），AC＝24cm，OB＝26cm，点P从点A出发，以1cm/s的速度向点C运动，点Q从点B同时出发，以3m/s的速度向点O运动．规定其中一个动点到达端点时，另一个动点也随之停止运动；从运动开始，设P（Q）点运动的时间为ts．

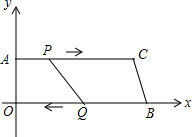
（1）求直线BC的函数解析式；

（2）当t为何值时，四边形AOQP是矩形？

21．（8分）先化简，再求值:     其中a＝

22．（10分）如图，反比例函数的图象经过点

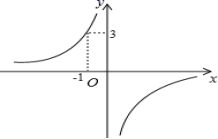
（1）求该反比例函数的解析式；

（2）当时，根据图象请直接写出自变量的取值范围．

23．（10分）已知：如图，在菱形ABCD 中，点E，O，F分别是边AB，AC，AD的中点，连接CE、CF、OE、OF．

（1）求证：△BCE≌△DCF；

（2）当AB与BC满足什么条件时，四边形AEOF正方形？请说明理由．

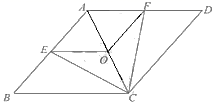
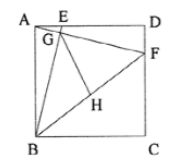
24．（12分）如图，点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点．

（1）如果图中线段都可画成有向线段，那么在这些有向线段所表示的向量中，与向量相等的向量是　   　；

（2）设＝，＝，＝．试用向量，或表示下列向量：＝　   　；＝　   　．

（3）求作：．（请在原图上作图，不要求写作法，但要写出结论）

参考答案

一、选择题(每小题3分,共30分)

1、D

2、C

3、B

4、B

5、C

6、A

7、C

8、B

9、A

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、10%

12、30.

13、5

14、对应角相等的三角形是全等三角形    假

15、

16、6    pq   

三、解下列各题(本大题共8小题，共72分)

17、

18、（1）x＝15；（2）x1＝，x2＝．

19、（1）答案见解析；（2）画图见解析，右，3；（3）①左， ②答案见解析.

20、 (1) y＝﹣4x+1； (2) 当t为6.5s时，四边形AOQP是矩形

21、-2.

22、（1）（2）或

23、（1）证明见解析；（2）AB⊥BC时，四边形AEOF正方形．

24、（1）；（2）+、+﹣；（3）如图所示见解析. ．