广东省东莞市南开实验学校2022-2023学年七下数学期末统考试题含答案

广东省东莞市南开实验学校2022-2023学年七下数学期末统考试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．如图，是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而成，其中AE=10，BE=24，则EF的长是（　　）

A．14 B．13 C．14 D．14

2．若关于x的一元二次方程kx2﹣2x+1＝0有两个不相等的实数根，则实数k的取值范围是(   )

A．k＞1 B．k＜1 C．k＞1且k≠0 D．k＜1且k≠0

3．以下列各组数为三角形的边长，能构成直角三角形的是（　　）

A．1，2，3 B．1，1， C．2，4，5 D．6，7，8

4．关于的一元二次方程有两个不相等的实数根，则的取值范围是（  ）

A． B． C．且 D．且

5．下列计算正确的是（　　）

A． B． C． D．﹣

6．对于函数y＝﹣2x+1，下列结论正确的是（　　）

A．它的图象必经过点（﹣1，3） B．它的图象经过第一、二、三象限

C．当时，y＞0 D．y值随x值的增大而增大

7．一名考生步行前往考场，10分钟走了总路程的，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1），则他到达考场所花的时间比一直步行提前了（　　）

A．20分钟    B．22分钟    C．24分钟    D．26分钟

8．下列各组数据中，能构成直角三角形的三边边长的是（  ）

A．l，2，3 B．6，8，10 C．2，3,4 D．9，13，17

9．若直角三角形两条直角边长分别为2, 3,则该直角三角形斜边上的高为(        )

A． B． C． D．

10．下列四个数中，大于而又小于的无理数是

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．分解因式：1﹣x2=　　　　．

12．如果关于的方程有实数解，那么的取值范围是_________.

13．小刚从家到学校的路程为2km，其中一段是lkm的平路，一段是lkm的上坡路．已知小刚在上坡、平路和下坡的骑车速度分别为akm/h，2akm/h，3akm/h，则小刚骑车从家到学校比从学校回家花费的时间多_____h．

14．在三角形中，点分别是的中点，于点，若，则________.

15．如图，四边形OABC是平行四边形，对角线OB在y轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线y1＝ 和y2＝ 的一支上，分别过点A、C作x轴的垂线，垂足分别为M和N，则有以下的结论：① ②阴影部分面积是（k1﹣k2）③当∠AOC＝90°时，|k1|＝|k2|；④若四边形OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．其中正确的结论是_____．

16．如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若，，则阴影部分的面积为__________．

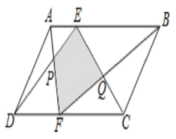
三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，在□ABCD 中，E、F为对角线AC上的两点，且AE=CF．

（1）求证：四边形DEBF是平行四边形；

（2）如果DE=3，EF=4，DF=5，求EB、DF两平行线之间的距离．

18．（8分）如图，在Rt△ABC中，∠ACB＝90°，点D，F分别在AB，AC上，CF＝CB．连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．

（1）求证：△BCD≌△FCE；

（2）若EF∥CD．求∠BDC的度数．

19．（8分）某项工程由甲乙两队分别单独完成，则甲队用时是乙队的1.5倍：若甲乙两队合作，则需12天完成，请问：

（1）甲，乙两队单独完成各需多少天；

（2）若施工方案是甲队先单独施工天，剩下工程甲乙两队合作完成，若甲队施工费用为每天1.5万元，乙队施工费为每天3.5万元求施工总费用（万元）关于施工时间（天）的函数关系式

（3）在（2）的方案下，若施工期定为15~18天内完成（含15和18天），如何安排施工方案使费用最少，最少费用为多少万元？

20．（8分）如图1，以直线MN上的线段BC为边作正方形ABCD，CH平分∠DCN，点E为射线BN上一点，连接AE，过点E作AE的垂线交射线CH于点F，探索AE与EF的数量关系。

(1)阅读下面的解答过程。并按此思路完成余下的证明过程

当点E在线段BC上，且点E为BC中点时，AB=EF

理由如下：

取AB中点P，達接PE

在正方形ABCD中，∠B=∠BCD=90°，AB=BC

∴△BPE等腰三角形，AP=BC

∴∠BPB=45°

∴∠APBE=135°

又因为CH平分∠DCN

∴∠DCF=45°

∴∠ECF=135°

∴∠APE=∠ECF

余下正明过程是：

(2)当点E为线段AB上任意一点时，如图2，结论“AE=EF”是否成立，如果成立，请给出证明过程；

(3)当点E在BC的延长线时，如图3，结论“AE=EF”是否仍然成立，如果成立，请在图3中画出必要的辅助线(不必说明理由)。

21．（8分）如图，菱形ABCD的边长为2，，点E为BC边的中点，点P为对角线AC上一动点，则PB+PE的最小值为_____．

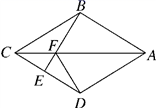
22．（10分）如图，在四边形ABCD中，AB＝AD，CB＝CD，E是CD上一点，BE交AC于点F，连接DF.

(1)求证：∠BAC＝∠DAC，∠AFD＝∠CFE；

(2)若AB∥CD，试证明四边形ABCD是菱形；

(3)在(2)的条件下，试确定E点的位置，使∠EFD＝∠BCD，并说明理由．

23．（10分）解分式方程或化简求值

（1） ；   

（2）先化简，再求值：，其中.

24．（12分）如图，在矩形ABCD中，AB＝8，BC＝6，点P、点E分别是边AB、BC上的动点，连结DP、PE．将 △ADP 与 △BPE分别沿DP与PE折叠，点A与点B分别落在点A′，B′处．

(1) 当点P运动到边AB的中点处时，点A′与点B′重合于点F处，过点C作CK⊥EF于K，求CK的长；

(2) 当点P运动到某一时刻，若P，A'，B'三点恰好在同一直线上，且A'B'＝4 ，试求此时AP的长．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、D

3、B

4、D

5、C

6、A

7、C

8、B

9、C

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、（1+x）（1﹣x）．

12、

13、

14、80°

15、①②④．

16、40

三、解下列各题(本大题共8小题，共72分)

17、（1）详见解析；（2）2.1.

18、（1）证明见解析；（2）90°.

19、（1）甲、乙两队单独完成分别需30天，20天；（2）y=0.5x+60;（3）甲队先施工10天，再甲乙合作8天，费用最低为55万元

20、（1）见解析；（2）成立，理由见解析；（3）成立，图形见解析

21、

22、（1）证明见解析（2）证明见解析（3）当BE⊥CD时，∠EFD＝∠BCD

23、；.

24、（1）；（2）,PA的长为2或1．