


山西省朔州怀仁县联考2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案
展开山西省朔州怀仁县联考2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
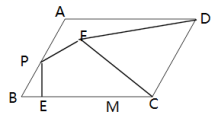
1.如图,已知平行四边形![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一动点,作
上一动点,作![]() 于点
于点![]() ,作
,作![]() (
(![]() 在
在![]() 右边)且始终保持
右边)且始终保持![]() ,连接
,连接![]() 、
、![]() ,设
,设![]() ,则
,则![]() 满足( )
满足( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
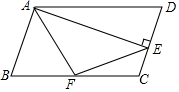
2.如图,▱ABCD中,![]() ,F是BC的中点,作
,F是BC的中点,作![]() ,垂足E在线段CD上,连接EF、AF,下列结论:
,垂足E在线段CD上,连接EF、AF,下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 中,一定成立的是
中,一定成立的是![]()
![]()
A.只有![]() B.只有
B.只有![]() C.只有
C.只有![]() D.
D.![]()
3.一辆客车从甲站开往乙站,中途曾停车休息了一段时间,如果用横轴表示时间t,纵轴表示客车行驶的路程s,如图所示,下列四个图像中能较好地反映s和t之间的函数关系的是( )
A.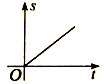 B.
B.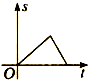 C.
C.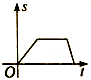 D.
D.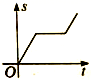
4.若分式方程![]() =2+
=2+![]() 的解为正数,则a的取值范围是( )
的解为正数,则a的取值范围是( )
A.a>4 B.a<4 C.a<4且a≠2 D.a<2且a≠0
5.把直线![]() 向下平移3个单位长度得到直线为( )
向下平移3个单位长度得到直线为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.当1<a<2时,代数式![]() +|1-a|的值是( )
+|1-a|的值是( )
A.-1 B.1 C.2a-3 D.3-2a
7.设正比例函数y=mx的图象经过点A(m,4),且y的值随x的增大而增大,则m=( )
A.2 B.-2 C.4 D.-4
8.慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中休息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.有以下说法:①快车速度是120千米/小时;②慢车到达乙地比快车到达乙地晚了0.5小时;③点C坐标(![]() ,100);④线段BC对应的函数表达式为y=120x﹣60(0.5≤x≤
,100);④线段BC对应的函数表达式为y=120x﹣60(0.5≤x≤![]() );其中正确的个数有( )
);其中正确的个数有( )
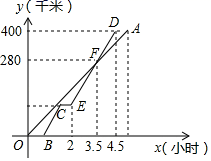
A.1 B.2 C.3 D.4
9.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
10.如图1,△ABC和△ADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图1.两次旋转的角度分别为( )
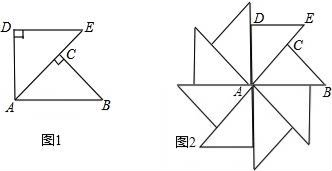
A.45°,90° B.90°,45° C.60°,30° D.30°,60°
11.爷爷在离家900米的公园锻炼后回家,离开公园20分钟后,爷爷停下来与朋友聊天10分钟,接着又走了15分钟回到家中.下面图形中表示爷爷离家的距离y(米)与爷爷离开公园的时间x(分)之间的函数关系是( )
A.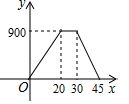 B.
B.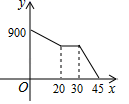
C.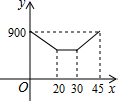 D.
D.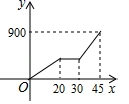
12.下列定理中,没有逆定理的是( )
A.对顶角相等 B.同位角相等,两直线平行
C.直角三角形的两锐角互余 D.直角三角形两直角边平方和等于斜边的平方
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.直线![]() 沿
沿![]() 轴平行的方向向下平移
轴平行的方向向下平移![]() 个单位,所得直线的函数解析式是_________
个单位,所得直线的函数解析式是_________
14.在一次数学单元考试中,某小组6名同学的成绩(单位:分)分别是:65,80,70,90,100,70。则这组数据的中位数分别是_________________________分。
15.阅读下面材料:
小明想探究函数![]() 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |
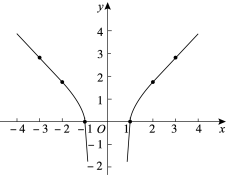
小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是 .请写出函数![]() 的一条性质: .
的一条性质: .
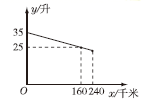
16.李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是 升.
17.小明用S2= ![]() [(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2]计算一组数据的方差,那么x1+x2+x3+…+x10=______.
[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2]计算一组数据的方差,那么x1+x2+x3+…+x10=______.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
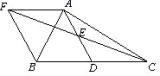
18.(5分)如图,在![]() 中,D是BC的中点,E是AD的中点,过点A作
中,D是BC的中点,E是AD的中点,过点A作![]() ,AF与CE的延长线相交于点F,连接BF.
,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)①若四边形AFBD是矩形,则![]() 必须满足条件_________;
必须满足条件_________;
②若四边形AFBD是菱形,则![]() 必须满足条件_________.
必须满足条件_________.
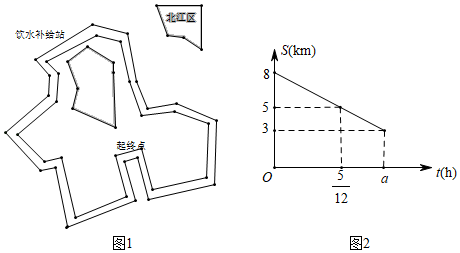
19.(5分) “2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行,小林参加了环绕湖8km的迷你马拉松项目(如图1),上午8:00起跑,赛道上距离起点5km处会设置饮水补给站,在比赛中,小林匀速前行,他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示
(1)求小林从起点跑向饮水补给站的过程中与t的函数表达式
(2)求小林跑步的速度,以及图2中a的值
(3)当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午8:55之前跑到终点,那么接下来一段路程他的速度至少应为多少?
20.(8分)先化简:![]() ,再从
,再从![]() 的范围内选取一个合适的整数作为
的范围内选取一个合适的整数作为![]() 的值代入求值.
的值代入求值.
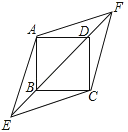
21.(10分)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
22.(10分)如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
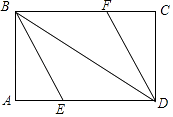
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
23.(12分)(1)计算: ![]() (2)计算:
(2)计算:![]()
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、D
4、C
5、D
6、B
7、A
8、D
9、B
10、A
11、B
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]() ;
;
14、75
15、如:因为函数值不可能为负,所以在x轴下方不会有图象; 当x≤-1时,y随x增大而减小,当x≥1时,y随x增大而增大
16、1
17、30
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)见解析;(2)①AB=AC;②∠BAC=90°
19、(1)![]() ;(2)速度为:
;(2)速度为:![]() km/h,a=
km/h,a=![]() ;(3)接下来一段路程他的速度至少为13.5km/h.
;(3)接下来一段路程他的速度至少为13.5km/h.
20、![]() .
.
21、(1)证明见解析(2)菱形
22、 (1)见解析;(2)见解析.
23、(1)15;(2)![]() .
.
2023-2024学年山西省朔州怀仁县联考数学九上期末复习检测模拟试题含答案: 这是一份2023-2024学年山西省朔州怀仁县联考数学九上期末复习检测模拟试题含答案,共8页。
山西省朔州怀仁县联考2023-2024学年八上数学期末检测试题含答案: 这是一份山西省朔州怀仁县联考2023-2024学年八上数学期末检测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,关于的一元二次方程的根的情况为,下列运算正确的是等内容,欢迎下载使用。
山东省潍坊联考2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份山东省潍坊联考2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。












