


山东省济南历下区七校联考2022-2023学年数学七年级第二学期期末教学质量检测试题含答案
展开山东省济南历下区七校联考2022-2023学年数学七年级第二学期期末教学质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
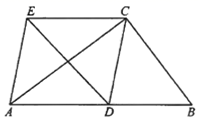
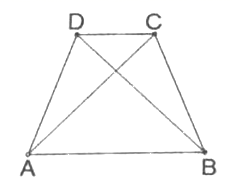
1.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 、
、![]() 为边作平行四边形
为边作平行四边形![]() ,则
,则![]() 长的最小值为( )
长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
3.如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A、C、E三点在同一水平直线上,则旗杆AB的高度为( )
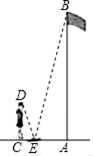
A.4.5m B.4.8m C.5.5m D.6 m
4.若分式![]() 有意义,则x的取值应该该满足( )
有意义,则x的取值应该该满足( )
A.x=![]() B.x=
B.x=![]() C.x≠
C.x≠![]() D.x≠
D.x≠![]()
5.已知![]() ,
,![]() ,
,![]() ,是一次函数
,是一次函数![]() (
(![]() 为常数)的图像的三点,则
为常数)的图像的三点,则![]() ,
,![]() ,
,![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.某校在体育健康测试中,有8名男生“引体向上”的成绩(单位:次)分别是:14,12,8,9,16,12,7,这组数据的中位数和众数分别是( )
A.10,12 B.12, 11 C.11,12 D.12,12
7.某商务酒店客房有![]() 间供客户居住.当每间房 每天定价为
间供客户居住.当每间房 每天定价为![]() 元时,酒店会住满;当每间房每天的定价每增加
元时,酒店会住满;当每间房每天的定价每增加![]() 元时,就会空闲一间房.如果有客户居住,宾馆需对居住的每间房每天支出
元时,就会空闲一间房.如果有客户居住,宾馆需对居住的每间房每天支出![]() 元的费用.当房价定为多少元时,酒店当天的利润为
元的费用.当房价定为多少元时,酒店当天的利润为![]() 元?设房价定为
元?设房价定为![]() 元,根据题意,所列方程是( )
元,根据题意,所列方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如果一个正多边形的内角和是这个正多边形外角和的2倍,那么这个正多边形是( )
A.等边三角形 B.正四边形 C.正六边形 D.正八边形
9.已知正比例函数y=kx,且y随x的增大而减少,则直线y=2x+k的图象是( )
A.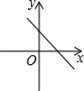 B.
B.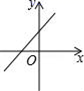 C.
C.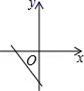 D.
D.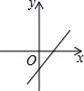
10.如图,在△ABC中,D,E,F分别是AB,BC,AC边的中点.如果添加一个条件,使四边形ADEF是菱形,则添加的条件为( )
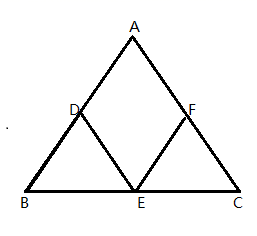
A.AB=AC B.AC=BC C.∠A=90° D.∠A=60°
二、填空题(本大题共有6小题,每小题3分,共18分)
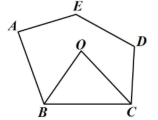
11.如图,在五边形![]() 中,
中,![]() ,
,![]() 和
和![]() 的平分线交于点
的平分线交于点![]() ,则
,则![]() 的度数为__________°.
的度数为__________°.
12.如图,在梯形![]() 中,
中,![]() ,对角线
,对角线![]() ,且
,且![]() ,则梯形
,则梯形![]() 的中位线的长为_________.
的中位线的长为_________.
13.往如图所示的地板中随意抛一颗石子(石子看作一个点),石子落在阴影区域的概率为___________

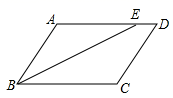
14.如图,在平行四边形ABCD中,E为AD边上一点,且AE=AB,若∠BED=160°,则∠D的度数为__________.
15.Rt△ABC中,∠C=90°,∠B=30°,则AC与AB两边的关系是_____.
16.有一面积为5![]() 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
三、解下列各题(本大题共8小题,共72分)
17.(8分)阅读材料I:
教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则:
的两根,则:![]() __ _,
__ _,![]() __ _,那么_
__ _,那么_![]() (请你完成以上的填空)
(请你完成以上的填空)
阅读材料:II
已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)若![]() 且
且![]() 则
则![]() ;
;
(3)已知![]() 且
且![]() .求
.求![]() 的值.
的值.
18.(8分)先化简,再求值:![]() ,其中
,其中![]()
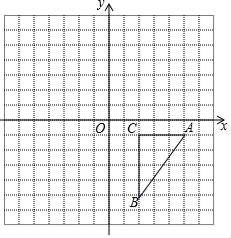
19.(8分)如图,方格纸中的每个小方格都是边长为1个单位长度的小正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A,B,C三点的坐标分别为(5,﹣1),(2,﹣5),(2,﹣1).
(1)把△ABC向上平移6个单位后得到△A1B1C1,画出△A1B1C1;
(2)画出△A2B2C2,使它与△ABC关于y轴对称;
(3)画出△A3B3C3,使它与△ABC关于原点中心对称.
20.(8分)如图,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,图①是沿
的中点,图①是沿![]() 将
将![]() 折叠,点
折叠,点![]() 落在
落在![]() 上,图②是绕点
上,图②是绕点![]() 将
将![]() 顺时针旋转
顺时针旋转![]() .
.
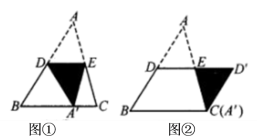
(1)在图①中,判断![]() 和
和![]() 形状.(填空)_______________________________________
形状.(填空)_______________________________________
(2)在图②中,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
21.(8分)如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
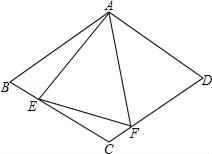
22.(10分) 写出同时具备下列两个条件的一次函数关系式_____.(写出一个即可)
(1)y随x的增大而减小;(2)图象经过点(1,﹣2).
23.(10分)移动营业厅推出两种移动电话计费方式:方案一,月租费用15元/元,本地通话费用0.2元/分钟,方案二,月租费用0元/元,本地通话费用0.3元/分钟.
(1)以x表示每个月的通话时间(单位:分钟),y表示每个月的电话费用(单位:元),分别表示出两种电话计费方式的函数表达式;
(2)问当每个月的通话时间为300分钟时,采用那种电话计费方式比较合算?
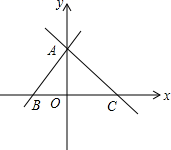
24.(12分)因为一次函数y=kx+b与y=-kx+b(k≠0)的图象关于y轴对称,所以我们定义:函数y=kx+b与y=-kx+b(k≠0)互为“镜子”函数.
(1)请直接写出函数y=3x-2的“镜子”函数:______________;
(2)如果一对“镜子”函数y=kx+b与y=-kx+b(k≠0)的图象交于点A,且与x轴交于B、C两点,如图所示,若△ABC是等腰直角三角形,∠BAC=90°,且它的面积是16,求这对“镜子”函数的解析式.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、D
4、C
5、C
6、C
7、D
8、C
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、1
13、![]()
14、40°.
15、AB=2AC.
16、1![]() 或1.
或1.
三、解下列各题(本大题共8小题,共72分)
17、(1)-3;-1;11;(2)![]() ;(3)
;(3)![]() .
.
18、![]() ,
,![]()
19、 (1)见解析;(2)见解析;(3)见解析.
20、(1)![]() 和
和![]() 均为等腰三角形;(2)四边形
均为等腰三角形;(2)四边形![]() 为平行四边形,证明详见解析.
为平行四边形,证明详见解析.
21、 (1)见解析;(2)![]() ;(3)见解析
;(3)见解析
22、y=-x-1
23、(1)方案一中通话费用关于时间的函数关系式为y=15+0.2x,(x≥0);方案二中通话费用关于时间的函数关系式为y=0.3x,(x≥0);(2)采用方案一电话计费方式比较合算.
24、(1)y=-3x-2;(2)y=-x+1与y=x+1
2023-2024学年山东省济南历下区七校联考数学九上期末经典试题含答案: 这是一份2023-2024学年山东省济南历下区七校联考数学九上期末经典试题含答案,共8页。试卷主要包含了下列事件中,属于随机事件的是,下列事件属于必然事件的是,中,,是边上的高,若,则等于等内容,欢迎下载使用。
山东省济南历下区七校联考2023-2024学年数学八上期末综合测试模拟试题含答案: 这是一份山东省济南历下区七校联考2023-2024学年数学八上期末综合测试模拟试题含答案,共7页。试卷主要包含了下列分解因式正确的是,2211年3月11日,里氏1,若分式的值为0,则x的值为,如图,下面推理中,正确的是等内容,欢迎下载使用。
山东省济南市历下区2022-2023学年七下数学期末达标检测模拟试题含答案: 这是一份山东省济南市历下区2022-2023学年七下数学期末达标检测模拟试题含答案,共6页。试卷主要包含了八边形的内角和为,在平面直角坐标系中,点M,下列各式中,运算正确的是等内容,欢迎下载使用。












