


山东省临沂市太平中学2022-2023学年七年级数学第二学期期末达标测试试题含答案
展开
这是一份山东省临沂市太平中学2022-2023学年七年级数学第二学期期末达标测试试题含答案,共7页。试卷主要包含了在平面直角坐标系中,点在第象限,已知,则下列不等式中不正确的是等内容,欢迎下载使用。
山东省临沂市太平中学2022-2023学年七年级数学第二学期期末达标测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.点![]() 关于原点的对称点
关于原点的对称点![]() 的坐标为( )A.
的坐标为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.下列数学符号中,属于中心对称图形的是( )A.
2.下列数学符号中,属于中心对称图形的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.如图,在
3.如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,则
,则![]() 等于( )
等于( )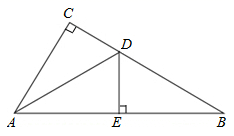 A.1.5° B.30° C.25° D.40°4.在平面直角坐标系中,点(–1,–2)在第( )象限.A.一 B.二 C.三 D.四5.如图,在
A.1.5° B.30° C.25° D.40°4.在平面直角坐标系中,点(–1,–2)在第( )象限.A.一 B.二 C.三 D.四5.如图,在![]() 中,点
中,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,若
的中点,若![]() ,则
,则![]() 的长度为( )
的长度为( )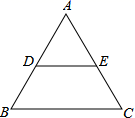 A.2 B.3 C.4 D.56.已知关于x的函数y=k(x-1)和y=
A.2 B.3 C.4 D.56.已知关于x的函数y=k(x-1)和y= ![]() (k≠0),它们在同一坐标系内的图象大致是( )A.
(k≠0),它们在同一坐标系内的图象大致是( )A.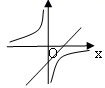 B.
B.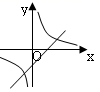 C.
C.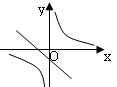 D.
D.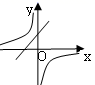 7.某中学规定学生的学期体育成绩满分为100,其中大课间及体育课外活动占60%,期末考试成绩古40%.小云的两项成绩(百分制)依次为84,1.小云这学期的体育成绩是( )A.86 B.88 C.90 D.928.已知一次函数y=kx+b的图象如图所示,则关于x的不等式
7.某中学规定学生的学期体育成绩满分为100,其中大课间及体育课外活动占60%,期末考试成绩古40%.小云的两项成绩(百分制)依次为84,1.小云这学期的体育成绩是( )A.86 B.88 C.90 D.928.已知一次函数y=kx+b的图象如图所示,则关于x的不等式![]() 的解集为
的解集为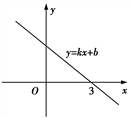 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,在平行四边形ABCD中,
9.如图,在平行四边形ABCD中,![]() ,
,![]() ,AC,BD相交于点O,
,AC,BD相交于点O,![]() ,交AD于点E,则
,交AD于点E,则![]() 的周长为
的周长为![]()
![]()
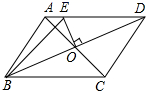 A.20cm B.18cm C.16cm D.10cm10.已知
A.20cm B.18cm C.16cm D.10cm10.已知![]() ,则下列不等式中不正确的是( )A.
,则下列不等式中不正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
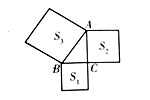
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,以
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,以![]() 的三边为边向外作正方形,其面积分别为
的三边为边向外作正方形,其面积分别为![]() ,且
,且![]() ,当
,当![]() __________时.
__________时.![]() .
. 12.若直线y=kx+b与直线y=2x平行,且与y轴相交于点(0,–3),则直线的函数表达式是__________.13. “如果 a=b,那么 a2=b2”,写出此命题的逆命题_______.14.如图,菱形
12.若直线y=kx+b与直线y=2x平行,且与y轴相交于点(0,–3),则直线的函数表达式是__________.13. “如果 a=b,那么 a2=b2”,写出此命题的逆命题_______.14.如图,菱形![]() 的边长为2,点
的边长为2,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的两个动点,且满足
上的两个动点,且满足![]() ,设
,设![]() 的面积为
的面积为![]() ,则
,则![]() 的取值范围是__.
的取值范围是__.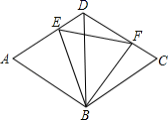 15.若一直角三角形的两直角边长为
15.若一直角三角形的两直角边长为![]() ,1,则斜边长为_____.16.如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为_____.
,1,则斜边长为_____.16.如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为_____.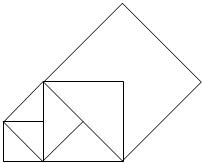 三、解下列各题(本大题共8小题,共72分)17.(8分)(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:①∠BEA =∠G,② EF=FG.(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
三、解下列各题(本大题共8小题,共72分)17.(8分)(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:①∠BEA =∠G,② EF=FG.(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.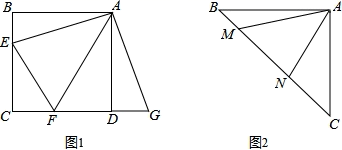 18.(8分)如图,已知A
18.(8分)如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]() (
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)求一次函数解析式及m的值;(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)求一次函数解析式及m的值;(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.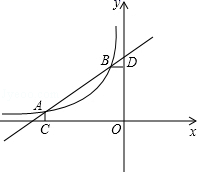 19.(8分)为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:甲林场乙林场购树苗数量销售单价购树苗数量销售单价不超过1000棵时4元/棵不超过2000棵时4元/棵超过1000棵的部分3.8元/棵超过2000棵的部分3.6元/棵设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;(2)分别求出y甲、y乙与x之间的函数关系式;(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么? 20.(8分)已知一次函数的图像经过点(2,1)和(0,-2).(1)求该函数的解析式;(2)判断点(-4,6)是否在该函数图像上. 21.(8分)俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.(1)求甲、乙两种品牌的足球的单价各是多少元?(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球? 22.(10分)某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,学校应如何购买更优惠? 23.(10分)四边形
19.(8分)为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:甲林场乙林场购树苗数量销售单价购树苗数量销售单价不超过1000棵时4元/棵不超过2000棵时4元/棵超过1000棵的部分3.8元/棵超过2000棵的部分3.6元/棵设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;(2)分别求出y甲、y乙与x之间的函数关系式;(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么? 20.(8分)已知一次函数的图像经过点(2,1)和(0,-2).(1)求该函数的解析式;(2)判断点(-4,6)是否在该函数图像上. 21.(8分)俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.(1)求甲、乙两种品牌的足球的单价各是多少元?(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球? 22.(10分)某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,学校应如何购买更优惠? 23.(10分)四边形![]() 是正方形,
是正方形,![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .当点G在BC边上时(如图1),易证DF-BE=EF.
.当点G在BC边上时(如图1),易证DF-BE=EF.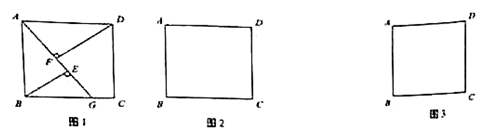 (1)当点
(1)当点![]() 在
在![]() 延长线上时,在图2中补全图形,写出
延长线上时,在图2中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,并证明;(2)当点
的数量关系,并证明;(2)当点![]() 在
在![]() 延长线上时,在图3中补全图形,写出
延长线上时,在图3中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,不用证明. 24.(12分)如图,在
的数量关系,不用证明. 24.(12分)如图,在![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.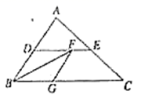 (1)求证:四边形
(1)求证:四边形![]() 是菱形;(2)若
是菱形;(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的周长. 参考答案 一、选择题(每小题3分,共30分)1、A2、B3、B4、C5、C6、A7、B8、B9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、
的周长. 参考答案 一、选择题(每小题3分,共30分)1、A2、B3、B4、C5、C6、A7、B8、B9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、y=2x–113、如果a2=b2,那么a=b.14、
12、y=2x–113、如果a2=b2,那么a=b.14、![]() .15、116、(
.15、116、(![]() )n. 三、解下列各题(本大题共8小题,共72分)17、(1)①见解析②见解析(1)
)n. 三、解下列各题(本大题共8小题,共72分)17、(1)①见解析②见解析(1)![]() 18、(1)当﹣4<x<﹣1时,一次函数大于反比例函数的值;(2)一次函数的解析式为y=
18、(1)当﹣4<x<﹣1时,一次函数大于反比例函数的值;(2)一次函数的解析式为y=![]() x+
x+![]() ;m=﹣2;(3)P点坐标是(﹣
;m=﹣2;(3)P点坐标是(﹣![]() ,
,![]() ).19、(1)5900,6000;(2)见解析;(3)当0≤x≤1000或x=3000时,两家林场购买一样,当1000<x<3000时,到甲林场购买合算;当x>3000时,到乙林场购买合算.20、 (1)y=
).19、(1)5900,6000;(2)见解析;(3)当0≤x≤1000或x=3000时,两家林场购买一样,当1000<x<3000时,到甲林场购买合算;当x>3000时,到乙林场购买合算.20、 (1)y=![]() x-2;(2)见解析.21、(1)甲种品牌的足球的单价为50元/个,乙种品牌的足球的单价为1元/个;(2)这所学校最多购买2个乙种品牌的足球.22、当购买的餐椅大于等于9少于32把时,到甲商场购买更优惠.23、(1)图详见解析,BE=DF+EF,证明详见解析;(2)图详见解析,EF=DF+BE.24、(1)见解析;(2)8.
x-2;(2)见解析.21、(1)甲种品牌的足球的单价为50元/个,乙种品牌的足球的单价为1元/个;(2)这所学校最多购买2个乙种品牌的足球.22、当购买的餐椅大于等于9少于32把时,到甲商场购买更优惠.23、(1)图详见解析,BE=DF+EF,证明详见解析;(2)图详见解析,EF=DF+BE.24、(1)见解析;(2)8.
相关试卷
这是一份山东省临沂市太平中学2023-2024学年数学九上期末达标测试试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,估计 ,的值应在等内容,欢迎下载使用。
这是一份2023-2024学年山东省临沂市太平中学八上数学期末学业水平测试模拟试题含答案,共8页。试卷主要包含了已知点在轴的负半轴,则点在,如图所示等内容,欢迎下载使用。
这是一份山东省临沂市太平中学2023-2024学年数学八上期末调研模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列运算中,计算结果正确的是等内容,欢迎下载使用。









