


北京六十六中学2022-2023学年数学七下期末调研模拟试题含答案
展开北京六十六中学2022-2023学年数学七下期末调研模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.若a≤1,则![]() 化简后为( )
化简后为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.抛物线y=(x﹣2)2+3的顶点坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
3.如图,在Rt△ABC中,∠ACB=90˚,D,E,F分别是AB,AC,AD的中点,若AB=8,则EF的长是( )
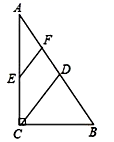
A.1 B.2 C.3 D.![]()
4.点![]() 在反比例函数
在反比例函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积是( ).
的面积是( ).
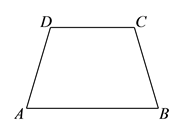
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
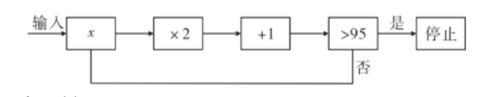
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,▱ABCD的对角线AC,BD交于点O,AC⊥AB,AB=![]() ,BO=3,那么AC的长为( )
,BO=3,那么AC的长为( )
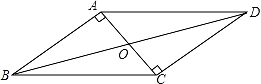
A.2![]() B.
B.![]() C.3 D.4
C.3 D.4
8.若关于 x 的一元二次方程![]() 有两个相等的实数根,则 b 的值为( )
有两个相等的实数根,则 b 的值为( )
A.0 B.4 C.0 或 4 D.0 或 4
9.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是( )
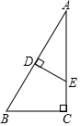
A.AE=3CE B.AE=2CE C.AE=BD D.BC=2CE
10.如图,在△ABC中,∠C=90°,点E是斜边AB的中点,ED⊥AB,且∠CAD:∠BAD=5:2,则∠BAC=( )
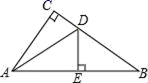
A.60° B.70° C.80° D.90°
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在等腰△ABC中,三边分别为a、b、c,其中a=4,b、c恰好是方程![]() 的两个实数根,则△ABC的周长为__________.
的两个实数根,则△ABC的周长为__________.
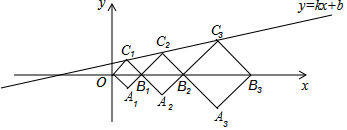
12.如图,在平面直角坐标系中,正方形OA1B1C1,B1A2B2C2,B2A3B3C3,…的顶点B1,B2,B3,…在x轴上,顶点C1,C2,C3,…在直线y=kx+b上,若正方形OA1B1C1,B1A2B2C2的对角线OB1=2,B1B2=3,则点C3的纵坐标是______________.
13.如果将直线![]() 平移,使其经过点
平移,使其经过点![]() ,那么平移后所得直线的表达式是__________.
,那么平移后所得直线的表达式是__________.
14.已知y=xm-2+3是一次函数,则m=________ .
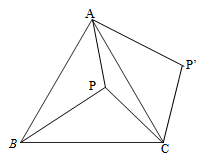
15.如图,![]() 是等边三角形
是等边三角形![]() 内一点,将线段
内一点,将线段![]() 绕点
绕点![]() 顺时针旋转60°得到线段
顺时针旋转60°得到线段![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为___________.
的面积为___________.
16.以正方形ABCD一边AB为边作等边三角形ABE,则∠CED=_____.
三、解下列各题(本大题共8小题,共72分)
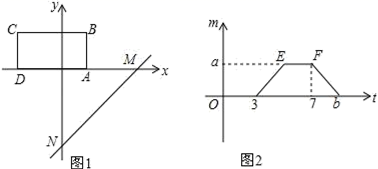
17.(8分)如图,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2,直线MN:y=x﹣4沿x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图2所示.
(1)点A的坐标为 ,矩形ABCD的面积为 ;
(2)求a,b的值;
(3)在平移过程中,求直线MN扫过矩形ABCD的面积S与t的函数关系式,并写出自变量t的取值范围.
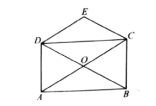
18.(8分)如图,O是矩形ABCD对角线的交点,作![]() ,
,![]() ,DE,CE相交于点E,求证:四边形OCED是菱形.
,DE,CE相交于点E,求证:四边形OCED是菱形.
19.(8分)已知:如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.

(1)求证:BC=BD;
(2)若BC=15,AD= 20,求AB和CD的长.
20.(8分)如图①,在平面直角坐标系中,直线![]() :
:![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() :
:![]() 交于点
交于点![]() ,以线段
,以线段![]() 为边在直线
为边在直线![]() 的下方作正方形
的下方作正方形![]() ,此时点
,此时点![]() 恰好落在
恰好落在![]() 轴上.
轴上.
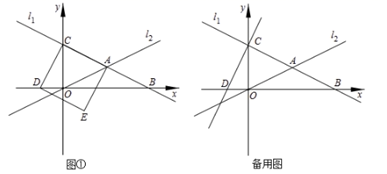
(1)求出![]() 三点的坐标.
三点的坐标.
(2)求直线![]() 的函数表达式.
的函数表达式.
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的一个动点,在平面内是否存在点
上的一个动点,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
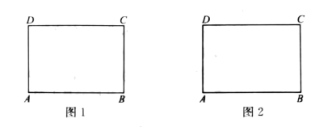
21.(8分)如图,矩形![]() 中,
中,![]() ,画出面积不相等的2个菱形,使菱形的顶点都在矩形的边上.
,画出面积不相等的2个菱形,使菱形的顶点都在矩形的边上.
22.(10分)如图,在平行四边形![]() 中,
中,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(2)求证:四边形![]() 是平行四边形.
是平行四边形.
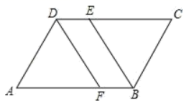
23.(10分)某商场计划购进一批书包,经市场调查发现:某种进货价格为30元的书包以40元的价格出售时,平均每月售出600个,并且书包的售价每提高1元,某月销售量就减少10个.
(1)若售价定为42元,每月可售出多少个?
(2)若书包的月销售量为300个,则每个书包的定价为多少元?
(3)当商场每月有10000元的销售利润时,为体现“薄利多销”的销售原则,你认为销售价格应定为多少?
24.(12分)某商场欲购进果汁饮料和碳酸饮料共60箱,两种饮料每箱的进价和售价如下表所示。设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价-总进价)。
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数解析式;
(2)求总利润w关于x的函数解析式;
(3)如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润。
饮料 | 果汁饮料 | 碳酸饮料 |
进价(元/箱) | 40 | 25 |
售价(元/箱) | 52 | 32 |
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、B
4、B
5、A
6、B
7、D
8、B
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、9或10.1
12、![]()
13、![]()
14、3
15、6+4![]()
16、30°或150°.
三、解下列各题(本大题共8小题,共72分)
17、(4)(4,7),3 ;(3)a=a=3![]() ,b=6;(3)S=
,b=6;(3)S=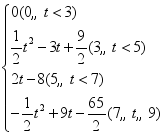 .
.
18、见解析
19、(1)证明:∵AB为⊙O的直径,AB⊥CD,∴![]() ,∴
,∴![]()
(2)![]() ,
,![]()
20、(1)![]()
![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,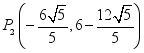 ,
,![]() .
.
21、见解析
22、(1)![]() ;(2)证明见解析.
;(2)证明见解析.
23、(1)580(个);(2)70(元);(3)为体现“薄利多销”的销售原则,我认为销售价格应定为50元.
24、(1)y=60-x;(2)w=5x+420;(3)该商场购进两种饮料分别为40箱和20箱时,能获得最大利润620元.
北京六十六中学2023-2024学年九上数学期末联考模拟试题含答案: 这是一份北京六十六中学2023-2024学年九上数学期末联考模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,如图,斜面AC的坡度,下列事件中,为必然事件的是,sin30°等于等内容,欢迎下载使用。
甘肃张掖甘州中学2022-2023学年数学七下期末调研模拟试题含答案: 这是一份甘肃张掖甘州中学2022-2023学年数学七下期末调研模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,如图,点、在函数,如果点P等内容,欢迎下载使用。
新疆乌鲁木齐第六十六中学2022-2023学年七下数学期末经典模拟试题含答案: 这是一份新疆乌鲁木齐第六十六中学2022-2023学年七下数学期末经典模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列事件中,是必然事件的是等内容,欢迎下载使用。












