


云南省保山市名校2022-2023学年七年级数学第二学期期末综合测试试题含答案
展开云南省保山市名校2022-2023学年七年级数学第二学期期末综合测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
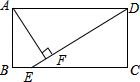
A.△AFD≌△DCE B.AF=![]() AD
AD
C.AB=AF D.BE=AD﹣DF
2.两个一次函数![]() 与
与![]() ,它们在同一直角坐标系中的图象可能是( )
,它们在同一直角坐标系中的图象可能是( )
A.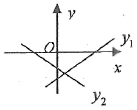 B.
B.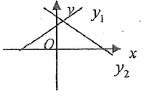
C.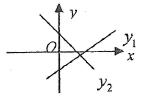 D.
D.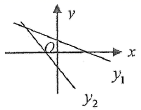
3.一次数学测验中,某学习小组六名同学的成绩(单位:分)分别是110,90,105,91,85,1.则该小组的平均成绩是( )
A.94分 B.1分 C.96分 D.98分
4.下面四个手机应用图标中是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
5.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,若四边形DEBC为菱形,则
上,若四边形DEBC为菱形,则![]() 的长度为( )
的长度为( )
A.7 B.9 C.3 D.4
6.化简![]() 的结果为( )
的结果为( )
A.﹣![]() B.﹣y C.
B.﹣y C.![]() D.
D.![]()
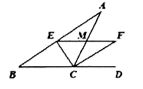
7.如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ( )
( )
A.75 B.100 C.120 D.125
8.下列所叙述的图形中,全等的两个三角形是( )
A.含有45°角的两个直角三角形 B.腰相等的两个等腰三角形
C.边长相等的两个等边三角形 D.一个钝角对应相等的两个等腰三角形
9.在▱ABCD中,对角线AC,BD相交于点O,AC=8,BD=10,那么BC的取值范围是( )
A.8<BC<10 B.2<BC<18 C.1<BC<8 D.1<BC<9
10.甲队修路120 m与乙队修路100 m所用天数相同,已知甲队比乙队每天多修10 m,设甲队每天修路xm.依题意,下面所列方程正确的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知关于![]() 的分式方程
的分式方程![]() 的解为负数,则
的解为负数,则![]() 的取值范围是 .
的取值范围是 .
12.▱ABCD中,AE⊥BD,∠EAD=60°,AE=2cm,AC+BD=14cm,则△OBC的周长是_____cm.
13.距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足: ![]() (其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面_________m.
(其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面_________m.
14.截止今年4月2日,华为官方应用市场“学习强国”APP下载量约为88300000次.将数88300000科学记数法表示为_______.
15.学校开展的“争做最美中学生”的一次演讲比赛中,编号分别为1,2,3,4,5的五位同学最后成绩如下表所示:

那么这五位同学演讲成绩的众数是_____,中位数是_____.
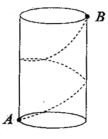
16.如图,圆柱体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为_____.
三、解下列各题(本大题共8小题,共72分)
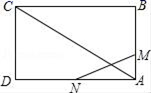
17.(8分)如图,已知矩形ABCD的边长AB=3cm,BC=6cm,某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动;同时,动点N从点D沿DA方向以2cm/s的速度向点A匀速运动.
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的![]() ?
?
(2)是否存在时刻t,使A、M、N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
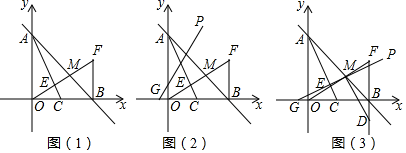
18.(8分)如图(1),在平面直角坐标系中,直线y=-x+m交y轴于点A,交x轴于点B,点C为OB的中点,作C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
(1)直接写出点F的坐标(用m表示);
(2)求证:OF⊥AC;
(3)如图(2),若m=2,点G的坐标为(-![]() ,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
①求k的取值范围;
②如图(3),若直线GP经过点M,过点M作GM的垂线交FB的延长线于点D,在平面内是否存在点Q,使四边形DMGQ为正方形?如果存在,请求出Q点坐标;如果不存在,请说明理由.
19.(8分)星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
| 进价(元/台) | 售价(元/台) |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中![]() 赚了多少钱?
赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
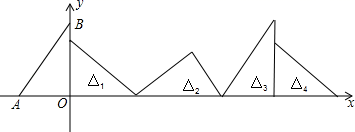
20.(8分)如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2020的直角顶点的坐标为_____.
21.(8分)已知y与x+2 成正比例,当x=4时,y=12.
(1)写出y与x之间的函数解析式;
(2)求当y=36时x的值;
(3)判断点(-7,-10)是否是函数图象上的点.
22.(10分)在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
| 第一次加热、降温过程 | … | ||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
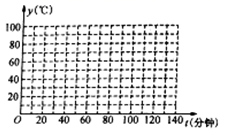
(1)根据表中数据在如图给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?
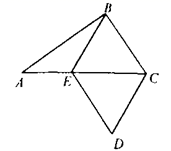
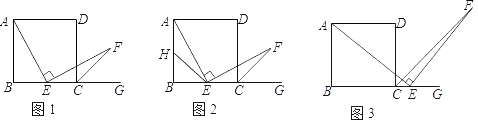
23.(10分)如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)如图2,取AB的中点H,连接HE,求证:AE=EF.
(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.
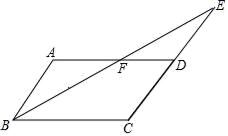
24.(12分)如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF,
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、D
5、A
6、D
7、B
8、C
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() 且
且![]() .
.
12、1.
13、7
14、![]() .
.
15、86, 1
16、10cm
三、解下列各题(本大题共8小题,共72分)
17、(1)1秒或2秒,(2)存在,![]() 秒或
秒或![]() 秒
秒
18、(1)(m,![]() m)(2)见解析(3)①0<k<6②(
m)(2)见解析(3)①0<k<6②(![]() ,-
,-![]() )
)
19、(1)1400元;(2)有三种方案:①防购买电饭煲23台,则购买电压锅27台;②购买电饭煲24台,则购买电压锅26台;③购买电饭煲1台,则购买电压锅1台.理由见解析;(3)购进电饭煲、电压锅各1台.
20、(8076,0)
21、 (1)y=2(x+2)=2x+4;
(2)x=16;
(3)点(-7,-10)是函数图象上的点.
22、(1)见解析;(2)第一次加热:![]() ,
,![]() ;第一次降温:
;第一次降温:![]() ,
,![]() ;(3)
;(3)![]() 分钟.
分钟.
23、(1)见解析;(2)成立,见解析.
24、①见解析②1
云南省保山市名校2023-2024学年九上数学期末学业水平测试试题含答案: 这是一份云南省保山市名校2023-2024学年九上数学期末学业水平测试试题含答案,共7页。试卷主要包含了答题时请按要求用笔,抛物线y=﹣3等内容,欢迎下载使用。
云南省保山市名校2023-2024学年九年级数学第一学期期末监测模拟试题含答案: 这是一份云南省保山市名校2023-2024学年九年级数学第一学期期末监测模拟试题含答案,共7页。试卷主要包含了若,则的值为,若反比例函数y=等内容,欢迎下载使用。
2023-2024学年云南省保山市名校数学八上期末教学质量检测试题含答案: 这是一份2023-2024学年云南省保山市名校数学八上期末教学质量检测试题含答案,共7页。试卷主要包含了下列计算正确的是,在平面直角坐标系中,点在等内容,欢迎下载使用。












