2022-2023学年陕西省西安高新逸翠园学校七年级数学第二学期期末质量检测模拟试题含答案

2022-2023学年陕西省西安高新逸翠园学校七年级数学第二学期期末质量检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

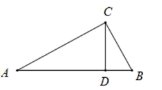
1．如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，CD⊥AB于D，则CD的长是(       )

A．5 B．7 C． D．

2．若关于的方程的解为正数，则的取值范围是（     ）

A．且 B．且  C． 且  D．

3．下列式子是分式的是(     ).

A． B． C． D．

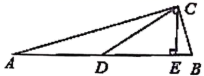
4．如图，在△ABC中，∠ACB＝90°，CE⊥AB，垂足为E，点D是边AB的中点，AB＝20，S△CAD＝30，则DE的长度是（　　）

A．6 B．8 C． D．9

5．为参加学校举办的“诗意校园•致远方”朗诵艺术大赛，八年级“屈原读书社”组织了五次选拔赛，这五次选拔赛中，小明五次成绩的平均数是90，方差是2；小强五次成绩的平均数也是90，方差是14.1．下列说法正确的是（　　）

A．小明的成绩比小强稳定

B．小明、小强两人成绩一样稳定

C．小强的成绩比小明稳定

D．无法确定小明、小强的成绩谁更稳定

6．将某个图形的各个顶点的横坐标都减去2，纵坐标保持不变，可将该图形（　　）

A．向左平移2个单位 B．向右平移2个单位

C．向上平移2个单位 D．向下平移2个单位

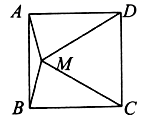
7．已知：如图，是正方形内的一点，且，则的度数为（    ）

A． B． C． D．

8．某中学书法兴趣小组10名成员的年龄情况如下表：

则该小组成员年龄的众数和中位数分别是（    ）

A．15，15 B．16，15 C．15，17 D．14，15

9．下列四组线段中，可以构成直角三角形的是（ ）

A．4,5,6 B．1.5,2，2.5 C．2,3,4 D．1，， 3

10．平南县某小区5月份随机抽取了15户家庭，对其用电情况进行了统计，统计情况如下（单位：度）：78，62，95，108，87，103，99，74，87，105，88，76，76，94，79.则用电量在71~80的家庭有（    ）

A．4户 B．5户 C．6户 D．7户

二、填空题(本大题共有6小题，每小题3分，共18分)

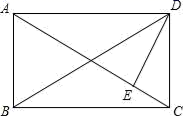
11．如图所示，在矩形ABCD中，DE⊥AC于E，∠ADE：∠EDC＝3：2，则∠BDE的度数是_____．

12．不等式组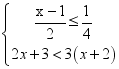的最小整数解是___________.

13．解一元二次方程x2＋2x－3＝0时，可转化为解两个一元一次方程，请写出其中的一个一元一次方程__________．

14．已知点及第二象限的动点，且．设的面积为，则关于的函数关系式为________．

15．若菱形的两条对角线长分别是6㎝和8㎝，则该菱形的面积是    ㎝1．

16．关于 x 的方程 x2+5x+m＝0 的一个根为﹣2，则另一个根是________ ．

三、解下列各题(本大题共8小题，共72分)

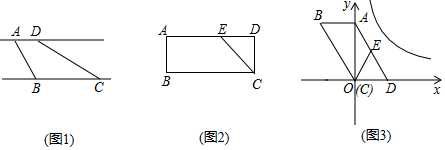
17．（8分）定义：有一组对边平行，有一个内角是它对角的一半的凸四边形叫做半对角四边形，如图1，直线，点，在直线上，点，在直线上，若，则四边形是半对角四边形．

（1）如图1，已知，，，若直线，之间的距离为，则AB的长是____，CD的长是______；

（2）如图2，点是矩形的边上一点，，．若四边形为半对角四边形，求的长；

（3）如图3，以的顶点为坐标原点，边所在直线为轴，对角线所在直线为轴，建立平面直角坐标系．点是边上一点，满足．

①求证：四边形是半对角四边形；

②当，时，将四边形向右平移个单位后，恰有两个顶点落在反比例函数的图象上，求的值．

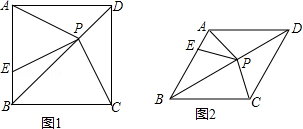
18．（8分）如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA=PE．

（1）求证：PC=PE；

（2）求∠CPE的度数；

（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，试探究∠CPE与∠ABC之间的数量关系，并说明理由．

19．（8分）有甲、乙两个不透明的布袋，甲袋中有两个完全相同的小球，分别标有数字1和-1；乙袋中有三个完全相同的小球，分别标有数字-1、0和1．小丽先从甲袋中随机取出一个小球，记录下小球上的数字为x；再从乙袋中随机取出一个小球，记录下小球上的数字为y，设点A的坐标为（x，y）．

（1）请用表格或树状图列出点A所有可能的坐标；

（1）求点A在反比例函数y=图象上的概率．

20．（8分）在某旅游景区上山的一条小路上，有一些断断续续的台阶，下图是其中的甲、乙两段台阶的示意图（图中的数字表示每一级台阶的高度，单位cm）．已知数据15、16、16、14、14、15的方差S甲2=，数据11、15、18、17、10、19的方差S乙2=．

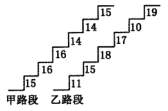
请你用学过的统计知识（平均数、中位数、方差和极差）通过计算，回答下列问题：

（1）两段台阶路有哪些相同点和不同点？

（2）哪段台阶路走起来更舒服？为什么？

（3）为方便游客行走，需要重新整修上山的小路．对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议．

21．（8分）计算题

（1）

（2）

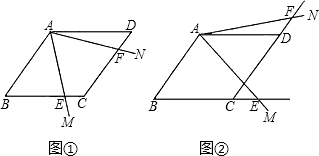
22．（10分）如图，菱形 ABCD 中，∠ABC＝60°，有一度数为 60°的∠MAN 绕点 A 旋转．

（1）如图①，若∠MAN 的两边 AM、AN 分别交 BC、CD 于点 E、F，则线段 CE、DF的大小关系如何？请证明你的结论．

（2）如图②，若∠MAN 的两边 AM、AN 分别交 BC、CD 的延长线于点 E、F，则线段CE、DF 还有（1）中的结论吗？请说明你的理由．

23．（10分）定义：直线与直线互为“友好直线”，如：直线与互为“友好直线”．

（1）点在直线的“友好直线”上，则________．

（2）直线上的点又是它的“友好直线”上的点，求点的坐标；

（3）对于直线上的任意一点，都有点在它的“友好直线”上，求直线的解析式．

24．（12分）计算：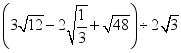

参考答案

一、选择题(每小题3分,共30分)

1、C

2、B

3、B

4、B

5、A

6、A

7、D

8、A

9、B

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、18°

12、-1

13、x＋3＝1(或x－1＝1)

14、

15、14

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）2；；（2）AD=3；（3）①证明见解析；②的值为为或．

18、（1）见解析；（2）∠EPC=90°；（3）∠ABC+∠EPC=180°．

19、（1）见解析；（1）．

20、（1）相同点：两段台阶路台阶高度的平均数相同；不同点：两段台阶路台阶高度的中位数、方差和极差均不相同；（2）甲段路走起来更舒服一些；（3）每个台阶高度均为15cm（原平均数）使得方差为1．

21、（1）（2）12

22、（1）CE=DF，证明见解析；（2）仍然有CE=DF，理由见解析.

23、（1）；（2）M（1，7）；（3）y=x-．

24、5