


2022-2023学年重庆八中学、九十五中学等学校七年级数学第二学期期末质量跟踪监视试题含答案
展开
这是一份2022-2023学年重庆八中学、九十五中学等学校七年级数学第二学期期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
2022-2023学年重庆八中学、九十五中学等学校七年级数学第二学期期末质量跟踪监视试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.若一个多边形的内角和为外角和的3倍,则这个多边形为 ( )A.八边形 B.九边形 C.十边形 D.十二边形2.如果![]() ,则a的取值范围是( )A.
,则a的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能正确反映这一函数关系的大致图像是( )A.
3.某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能正确反映这一函数关系的大致图像是( )A.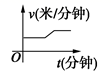 B.
B.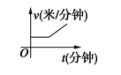 C.
C.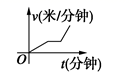 D.
D.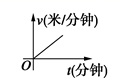 4.下列图形中,不是中心对称图形的是( )A.平行四边形 B.矩形 C.菱形 D.等边三角形5.下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,照此规律排列下去,则第8个图中小正方形的个数是( )
4.下列图形中,不是中心对称图形的是( )A.平行四边形 B.矩形 C.菱形 D.等边三角形5.下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,照此规律排列下去,则第8个图中小正方形的个数是( )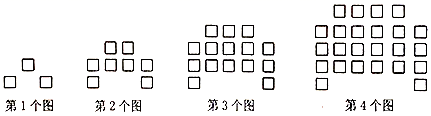 A.48 B.63 C.80 D.996.若
A.48 B.63 C.80 D.996.若![]() 在实数范围内有意义,则a的取值范围是( )A.a≥
在实数范围内有意义,则a的取值范围是( )A.a≥![]() B.a≤
B.a≤![]() C.a>
C.a>![]() D.a<
D.a<![]() 7.小强同学投掷 30 次实心球的成绩如下表所示:
7.小强同学投掷 30 次实心球的成绩如下表所示: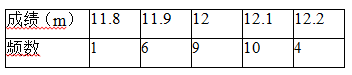 由上表可知小强同学投掷 30 次实心球成绩的众数与中位数分别是( )A.12m,11.9m B.12m,12.1m C.12.1m,11.9m D.12.1m,12m8.▱ABCD中,如果
由上表可知小强同学投掷 30 次实心球成绩的众数与中位数分别是( )A.12m,11.9m B.12m,12.1m C.12.1m,11.9m D.12.1m,12m8.▱ABCD中,如果![]() ,那么
,那么![]() 、
、![]() 的值分别是
的值分别是![]()
![]() A.
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]() 9.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
9.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论: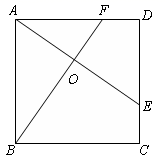 (1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)
(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)![]() 中正确的有A.4个 B.3个 C.2个 D.1个10.估计
中正确的有A.4个 B.3个 C.2个 D.1个10.估计![]() ﹣
﹣![]() ÷2的运算结果在哪两个整数之间( )A.0和1 B.1和2 C.2和3 D.3和4二、填空题(本大题共有6小题,每小题3分,共18分)11.要使分式
÷2的运算结果在哪两个整数之间( )A.0和1 B.1和2 C.2和3 D.3和4二、填空题(本大题共有6小题,每小题3分,共18分)11.要使分式![]() 的值为0,则x的值为____________.12.函数y=
的值为0,则x的值为____________.12.函数y=![]() 与y=x-1的图象的交点坐标为(x0,y0),则
与y=x-1的图象的交点坐标为(x0,y0),则![]() 的值为_____________.13.如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____.
的值为_____________.13.如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____. 14.已知菱形ABCD的对角线AC=10,BD=24,则菱形ABCD的面积为__________。15.如图,在矩形
14.已知菱形ABCD的对角线AC=10,BD=24,则菱形ABCD的面积为__________。15.如图,在矩形![]() 中,
中,![]() 于点
于点![]() ,对角线
,对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() __________.
__________.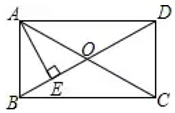 16.如图,菱形
16.如图,菱形![]() 的边长为2,点
的边长为2,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的两个动点,且满足
上的两个动点,且满足![]() ,设
,设![]() 的面积为
的面积为![]() ,则
,则![]() 的取值范围是__.
的取值范围是__.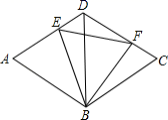 三、解下列各题(本大题共8小题,共72分)17.(8分)甲、乙两位同学参加数学竞赛辅导,三项培训内容的考试成绩如下表,现要选拔一人参赛.(1)若按三项考试成绩的平均分选拔,应选谁参赛;(2)若代数、几何、综合分别按20%、30%、50%的比例计算平均分,应选谁参赛. 代数几何综合甲859275乙708390 18.(8分)如图,在平行四边形
三、解下列各题(本大题共8小题,共72分)17.(8分)甲、乙两位同学参加数学竞赛辅导,三项培训内容的考试成绩如下表,现要选拔一人参赛.(1)若按三项考试成绩的平均分选拔,应选谁参赛;(2)若代数、几何、综合分别按20%、30%、50%的比例计算平均分,应选谁参赛. 代数几何综合甲859275乙708390 18.(8分)如图,在平行四边形![]() 中,点
中,点![]() 、
、![]() 别在
别在![]() ,
,![]() 上,且
上,且![]() .(1)如图①,求证:四边形
.(1)如图①,求证:四边形![]() 是平行四边形;(2)如图②,若
是平行四边形;(2)如图②,若![]() ,且
,且![]() .
.![]() ,求平行四边形
,求平行四边形![]() 的周长.
的周长.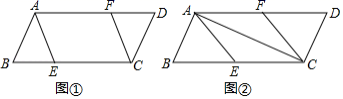 19.(8分)观摩、学习是我们生活的一部分,而在观摩中与展览品保持一定的距离是一种文明的表现.某学校数学业余学习小组在平面直角坐标系xOy有关研讨中,将到线段PQ所在的直线距离为
19.(8分)观摩、学习是我们生活的一部分,而在观摩中与展览品保持一定的距离是一种文明的表现.某学校数学业余学习小组在平面直角坐标系xOy有关研讨中,将到线段PQ所在的直线距离为![]() 的直线,称为直线PQ的“观察线”,并称观察线上到P、Q两点距离和最小的点L为线段PQ的“最佳观察点”.(1)如果P(1,
的直线,称为直线PQ的“观察线”,并称观察线上到P、Q两点距离和最小的点L为线段PQ的“最佳观察点”.(1)如果P(1,![]() ),Q(4,
),Q(4,![]() ),那么在点A(1,0),B(
),那么在点A(1,0),B(![]() ,2
,2![]() ),C(
),C(![]() ,3)中,处在直线PQ的“观察线”上的是点 ;(2)求直线y=
,3)中,处在直线PQ的“观察线”上的是点 ;(2)求直线y=![]() x的“观察线”的表达式;(3)若M(0,﹣1),N在第二象限,且MN=6,当MN的一个“最佳观察点”在y轴正半轴上时,直接写出点N的坐标;并按逆时针方向联结M、N及其所有“最佳观察点”,直接写出联结所围成的多边形的周长和面积. 20.(8分)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一棵树的树梢,问小鸟至少飞行几米?
x的“观察线”的表达式;(3)若M(0,﹣1),N在第二象限,且MN=6,当MN的一个“最佳观察点”在y轴正半轴上时,直接写出点N的坐标;并按逆时针方向联结M、N及其所有“最佳观察点”,直接写出联结所围成的多边形的周长和面积. 20.(8分)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一棵树的树梢,问小鸟至少飞行几米? 21.(8分)四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求DH的长.
21.(8分)四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求DH的长. 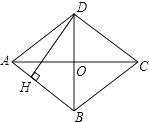 22.(10分)下表是某网络公司员工月收人情况表.月收入(元)
22.(10分)下表是某网络公司员工月收人情况表.月收入(元)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 人数
人数![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (1)求此公司员工月收人的中位数;(2)小张求出这个公司员工月收人平均数为
(1)求此公司员工月收人的中位数;(2)小张求出这个公司员工月收人平均数为![]() 元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好? 23.(10分)计算(1)
元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好? 23.(10分)计算(1)![]() (2)
(2)![]() . 24.(12分)现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.(1)根据题意,填写下表:快递物品重量(千克)0.5134…甲公司收费(元) 22 …乙公司收费(元)11 5167… (2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、A4、D5、C6、A7、D8、B9、B10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、-2.12、
. 24.(12分)现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.(1)根据题意,填写下表:快递物品重量(千克)0.5134…甲公司收费(元) 22 …乙公司收费(元)11 5167… (2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、A4、D5、C6、A7、D8、B9、B10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、-2.12、![]() 13、
13、![]() 14、12015、
14、12015、![]() 16、
16、![]() . 三、解下列各题(本大题共8小题,共72分)17、(1)选择甲;(2)选择乙.18、 (1)见解析;(2)16.19、 (1)A,B; (1)直线y=
. 三、解下列各题(本大题共8小题,共72分)17、(1)选择甲;(2)选择乙.18、 (1)见解析;(2)16.19、 (1)A,B; (1)直线y=![]() x的“观察线”的解析式为y=
x的“观察线”的解析式为y=![]() x﹣1或y=
x﹣1或y=![]() x+1;(3)围成的图形是菱形MQNQ′,这个菱形的周长8
x+1;(3)围成的图形是菱形MQNQ′,这个菱形的周长8![]() ,这个菱形的面积6
,这个菱形的面积6![]() .20、小鸟至少飞行10米.21、
.20、小鸟至少飞行10米.21、![]() 22、(1)3000元;(2)不合适,利用中位数更好.23、4+
22、(1)3000元;(2)不合适,利用中位数更好.23、4+![]() ;6+
;6+![]() 24、(1)11,19,52,1;(2)
24、(1)11,19,52,1;(2)![]() ;y2=16x+3;(3)当3<x<3时,小明应选择乙公司省钱;当x=3时,两家公司费用一样;当x>3,小明应选择甲公司省钱.
;y2=16x+3;(3)当3<x<3时,小明应选择乙公司省钱;当x=3时,两家公司费用一样;当x>3,小明应选择甲公司省钱.
相关试卷
这是一份2023-2024学年重庆巴川量子中学八上数学期末质量跟踪监视试题含答案,共8页。试卷主要包含了点P,如图,≌,下列结论正确的是等内容,欢迎下载使用。
这是一份重庆市渝北中学2023-2024学年八上数学期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,估算的值等内容,欢迎下载使用。
这是一份重庆合川区南屏中学2023-2024学年数学八上期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了下列命题,是真命题的是,数字用科学记数法表示为,下列表述中,能确定准确位置的是等内容,欢迎下载使用。








