2022-2023学年辽宁省抚顺抚顺县联考数学七年级第二学期期末质量检测模拟试题含答案

2022-2023学年辽宁省抚顺抚顺县联考数学七年级第二学期期末质量检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．如图，抛物线与直线经过点，且相交于另一点，抛物线与轴交于点，与轴交于另一点，过点的直线交抛物线于点，且轴，连接，当点在线段上移动时（不与、重合），下列结论正确的是（  ）

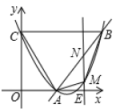
A． B．

C． D．四边形的最大面积为13

2．如图，在中，，，垂足为，点是边的中点，，，则（　　）

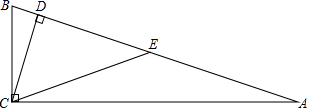
A．8 B．7.5 C．7 D．6

3．如图直线l1：y=ax+b，与直线l2：y=mx+n交于点A（1，3），那么不等式ax+b＜mx+n的解集是（　　）

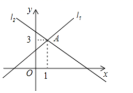
A．x＞3      B．x＜3       C．x＞1    D．x＜1

4．关于的一元二次方程有两个相等的实数根，则的值（    ）

A．2 B．3 C． D．

5．如图是我国一位古代数学家在注解《周髀算经》时给出的，曾被选为2002年在北京召开的国际数学家大会的会徽，它通过对图形的切割、拼接，巧妙地证明了勾股定理，这位伟大的数学家是（   ）

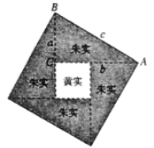
A．杨辉 B．刘徽 C．祖冲之 D．赵爽

6．已知直线y=mx+n（m，n为常数）经过点（0，﹣2）和（3，0），则关于x的方程mx+n=0的解为（　　）

A．x=0 B．x=1 C．x=﹣2 D．x=3

7．弹簧挂上物体后伸长，已知一弹簧的长度（cm）与所挂物体的质量（kg）之间的关系如下表：下列说法错误的是（  ）

A．在没挂物体时，弹簧的长度为10cm

B．弹簧的长度随物体的质量的变化而变化，物体的质量是因变量，弹簧的长度是自变量

C．如果物体的质量为mkg，那么弹簧的长度ycm可以表示为y=2.5m+10

D．在弹簧能承受的范围内，当物体的质量为4kg时，弹簧的长度为20cm

8．下列式子中，可以取和的是（   ）

A． B． C． D．

9．下列事件属于必然事件的是（）

A．抛掷两枚硬币，结果一正一反

B．取一个实数的值为 1

C．取一个实数

D．角平分线上的点到角的两边的距离相等

10．下列图形具有稳定性的是（　　）

A．三角形 B．四边形 C．五边形 D．六边形

二、填空题(本大题共有6小题，每小题3分，共18分)

11．正比例函数的图象经过点（-1,2），则此函数的表达式为___________.

12．五边形从某一个顶点出发可以引_____条对角线．

13．使为整数的的值可以是________（只需填一个）.

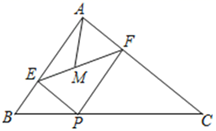
14．如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值是________ ．

15．．在平面直角坐标系中，若点M（1，3）与点N（x，3）之间的距离是5，则x的值是____________．

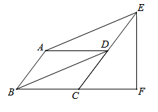
16．如图，平行四边形ABCD中，∠ABC＝60°，E，F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，CF＝1，求AB的长是___________.

三、解下列各题(本大题共8小题，共72分)

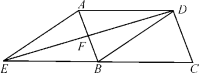
17．（8分）如图，在平行四边形ABCD中，DB＝DA，∠ADB的平分线交AB于点F，交CB的延长线于点E，连接AE.

(1)求证：四边形AEBD是菱形；

 (2)若DC＝，EF：BF＝3，求菱形AEBD的面积．

18．（8分）昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款人数的比为1：1．

请结合以上信息解答下列问题．

（1）a＝　   　，本次调查样本的容量是　   　；

（2）先求出C组的人数，再补全“捐款人数分组统计图1”；

（3）根据统计情况，估计该校参加捐款的4100名学生有多少人捐款在20至40元之间．

19．（8分）解方程：-=-1．

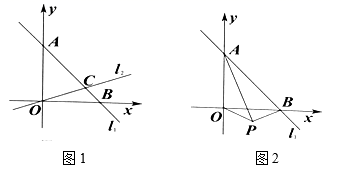
20．（8分）已知：如图1，在平面直角坐标系中，直线与坐标轴分别相交于点，与直线相交于点.

（1）求点的坐标；

（2）若平行于轴的直线交于直线于点，交直线于点，交轴于点，且，求的值；

（3）如图2，点是第四象限内一点，且，连接，探究与之间的位置关系，并证明你的结论.

21．（8分）如图，在平面直角坐标系xOy中，已知直线AB：yx+4交x轴于点A，交y轴于点B．直线CD：yx﹣1与直线AB相交于点M，交x轴于点C，交y轴于点D．

（1）直接写出点B和点D的坐标；

（2）若点P是射线MD上的一个动点，设点P的横坐标是x，△PBM的面积是S，求S与x之间的函数关系；

（3）当S＝20时，平面直角坐标系内是否存在点E，使以点B、E、P、M为顶点的四边形是平行四边形？若存在，请直接写出所有符合条件的点E的坐标；若不存在，说明理由．

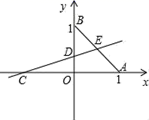
22．（10分）已知：如图，平面直角坐标系xOy中，B（0，1），OB＝OC＝OA，A、C分别在x轴的正负半轴上．过点C的直线绕点C旋转，交y轴于点D，交线段AB于点E．

（1）求∠OAB的度数及直线AB的解析式；

（2）若△OCD与△BDE的面积相等，求点D的坐标．

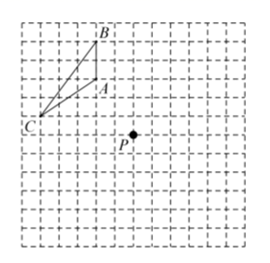
23．（10分）在下列网格图中，每个小正方形的边长均为个单位长度．已知在网格图中的位置如图所示．

（1）请在网格图中画出向右平移单位后的图形，并直接写出平移过程中线段扫过的面积；

（2）请在网格图中画出以为对称中心的图形.(保留作图痕迹)

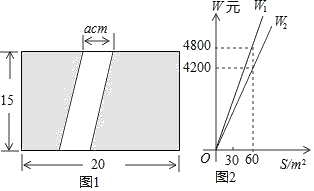
24．（12分）如图1，为美化校园环境，某校计划在一块长为20m，宽为15m的长方形空地上修建一条宽为a（m）的甬道，余下的部分铺设草坪建成绿地．

（1）甬道的面积为　   　m2，绿地的面积为　   　m2（用含a的代数式表示）；

（2）已知某公园公司修建甬道，绿地的造价W1（元），W2（元）与修建面积S之间的函数关系如图2所示．①园林公司修建一平方米的甬道，绿地的造价分别为　   　元，　   　元．②直接写出修建甬道的造价W1（元），修建绿地的造价W2（元）与a（m）的关系式；③如果学校决定由该公司承建此项目，并要求修建的甬道宽度不少于2m且不超过5m，那么甬道宽为多少时，修建的甬道和绿地的总造价最低，最低总造价为多少元？

参考答案

一、选择题(每小题3分,共30分)

1、C

2、B

3、D

4、A

5、D

6、D

7、B

8、C

9、D

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、y=-2x

12、1

13、1．

14、

15、－4或1

16、1

三、解下列各题(本大题共8小题，共72分)

17、（1）见解析；（2）1.

18、 (1)20，100；（2）见解析；（3）3060人

19、x=-1

20、（1）；（2）或；(3),理由见解析。

21、（1）B（0，4），D（0，－1）；（2）S（x＞－2）；（3）存在，满足条件的点E的坐标为（8，）或（﹣8，）或（﹣2，）．

22、（1）45°，y＝﹣x+1；（2）（0，）．

23、（1）18；（1）图形见详解.

24、（1）15a、（300﹣15a）；（2）①①80、70；；②W1＝80×15a＝1200a，W2＝70（300﹣15a）＝﹣1050a+21000；③甬道宽为2米时，修建的甬道和绿地的总造价最低，最低总造价为21300元；