培优专题08 全等三角形十大模型之截长补短和手拉手模型-2023-2024学年八年级数学上册精选专题培优讲与练（人教版）

培优专题08 全等三角形的十大模型之

截长补短和手拉手模型

◎模型七：截长补短法

【模型分析】截长补短的方法适用于求证线段的和差倍分关系。截长：指在长线段中截取一段等于已知线段；补短：指将短线段延长，延长部分等于已知线段。该类题目中常出现等腰三角形、角平分线等关键词句，可以采用截长补短法构造全等三角形来完成证明过程，截长补短法（往往需证2次全等）。

【模型图示】

（1）截长：在较长线段上截取一段等于某一短线段，再证剩下的那一段等于另一短线段。

例：如图，求证BE+DC=AD

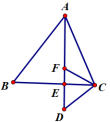
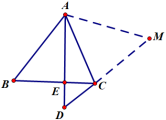
方法：①在AD上取一点F，使得AF=BE，证DF=DC；②在AD上取一点F，使DF=DC，证AF=BE

（2）补短：将短线段延长，证与长线段相等

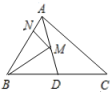
1．（2022·全国·八年级课时练习）如图，在中，，，平分，、分别是、上的动点，当最小时，的度数为(　　)

A． B． C． D．

2．（2022·全国·八年级课时练习）如图，已知四边形ABCD中，AD∥BC，若∠DAB的平分线AE交CD于E，连接BE，且BE恰好平分∠ABC，则AB的长与AD+BC的大小关系是（　　）

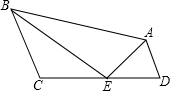
A．AB＞AD+BC B．AB＜AD+BC C．AB＝AD+BC D．无法确定

3．（2022·江苏·八年级专题练习）如图，为等边三角形，若，则__________（用含的式子表示）．

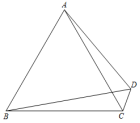
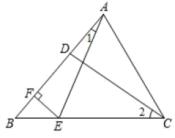
4．（2021··九年级专题练习）如图，△ABC中，E在BC上，D在BA上，过E作EF⊥AB于F，∠B＝∠1+∠2，AB＝CD，BF＝，则AD的长为________．

5．（2022·江苏·八年级课时练习）如图，在锐角中，，点，分别是边，上一动点，连接交直线于点．

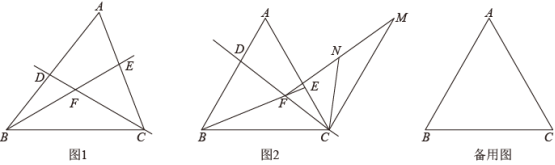
(1)如图1，若，且，，求的度数；

(2)如图2，若，且，在平面内将线段绕点顺时针方向旋转得到线段，连接，点是的中点，连接．在点，运动过程中，猜想线段，，之间存在的数量关系，并证明你的猜想．

◎模型八： 手拉手模型

【模型分析】

将两个三角形绕着公共顶点（即头）旋转某一角度后能完全重合，则这两个三角形构成手拉手全等，也叫旋转型全等，常用“边角边”判定定理证明全等。

【模型图示】

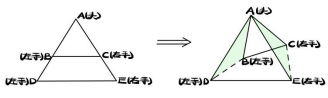
公共顶点A记为“头”，每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”，第二个顶点记为“右手”。对应操作：左手拉左手（即连结BD），右手拉右手（即连结CE），得。

【常见模型】

（等腰）

（等边）

（等腰直角）

6．（2022·江苏·八年级专题练习）如图，C为线段AE上一动点（不与点，重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下结论错误的是（       ）

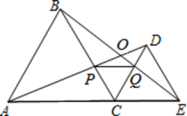
A．∠AOB=60° B．AP=BQ

C．PQ∥AE D．DE=DP

7．（2022·全国·八年级课时练习）如图，正和正中，B、C、D共线，且，连接和相交于点F，以下结论中正确的有（       ）个

①   ②连接，则平分   ③   ④

A．4 B．3 C．2 D．1

8．（2022·全国·八年级课时练习）如图，在Rt△ABC中，∠ABC＝90°，AB＝BC，点D为三角形右侧外一点．且∠BDC＝45°．连接AD，若△ACD的面积为，则线段CD的长度为 ___．

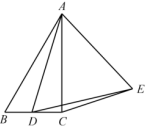
9．（2020·湖北·武汉市二桥中学八年级阶段练习）在中，，，，点D是直线BC上一动点，连接AD，在直线AD的右恻作等边，连接CE，当线段CE的长度最小时，则线段CD的长度为__________．

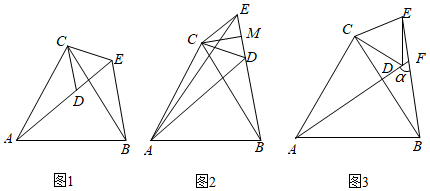
10．（2022·江苏·八年级课时练习）△ACB和△DCE是共顶点C的两个大小不一样的等边三角形．

(1)问题发现：

如图1，若点A，D，E在同一直线上，连接AE，BE．

①求证：△ACD≌△BCE；

②求∠AEB的度数．

(2)类比探究：如图2，点B、D、E在同一直线上，连接AE，AD，BE，CM为△DCE中DE边上的高，请求∠ADB的度数及线段DB，AD，DM之间的数量关系，并说明理由．

(3)拓展延伸：如图3，若设AD（或其延长线）与BE的所夹锐角为α，则你认为α为多少度，并证明．