


- 【同步练习】高中数学人教A版(2019)必修第二册--6.2.4向量的数量积 课时作业(含解析) 试卷 0 次下载
- 【同步练习】高中数学人教A版(2019)必修第二册--6.3.1平面向量基本定理 课时作业(含解析) 试卷 0 次下载
- 【同步练习】高中数学人教A版(2019)必修第二册--6.3.4平面向量数乘运算的坐标表示 课时作业(含解析) 试卷 0 次下载
- 【同步练习】高中数学人教A版(2019)必修第二册--6.3.5平面向量数量积的坐标表示 课时作业(含解析) 试卷 0 次下载
- 【同步练习】高中数学人教A版(2019)必修第二册--6.4.1平面几何中的向量方法 课后检测(含解析) 试卷 0 次下载
【同步练习】高中数学人教A版(2019)必修第二册--6.3.2平面向量的正交分解及坐标表示+6.3.3平面向量加减运算的坐标表示 课时作业(含解析)
展开6.3.2 平面向量的正交分解及坐标表示6.3.3 平面向量加、减运算的坐标表示
必备知识基础练
1.已知向量a=(1,2),b=(3,4),则a-b=( )
A.(2,6) B.(-2,6)
C.(4,6) D.(-2,-2)
2.已知点A(-2,3),B(3,2),则向量的坐标为( )
A.(-5,1) B.(5,-1)
C.(1,5) D.(-1,-5)
3.若向量=(4,2),=(-1,-3),则=( )
A.(3,-1) B.(-3,1)
C.(-3,-1) D.(3,1)
4.已知平面直角坐标系内△ABC三个顶点的坐标分别为A(-1,1),B(2,3),C(-6,5),D为BC边的中点,则=( )
A.(-3,2) B.(-1,3)
C.(-3,5) D.(-2,4)
5.向量a,b满足a+b=(-1,5),a-b=(5,-3),则b=( )
A.(3,4) B.(-3,4)
C.(3,-4) D.(-3,-4)
6.(多选)已知a=(1,3),b=(-2,1),下列计算正确的是( )
A.a+b=(-1,4) B.a-b=(3,2)
C.b-a=(1,2) D.-a-b=(1,2)
7.已知向量=(3,-2),=(-5,-1),则向量的坐标是________.
8.已知=(1,2),A(3,4),则B点坐标是________.
关键能力综合练
1.向量e1、e2、a在正方形网格中的位置如图所示,若a=λ1e1+λ2e2(λ1,λ2∈R),则λ1·λ2=( )

A.-4 B.-2C.2 D.4
2.已知点A(1,3),B(4,-1),则与向量的方向相反的单位向量是( )
A.(-,) B.(-,)C.(,-) D.(,)
3.在平行四边形ABCD中,AC为一条对角线.若=(2,4),=(1,3),则=( )
A.(-2,4) B.(-3,-5)C.(3,5) D.(-3,-7)
4.(多选)已知平行四边形的三个顶点的坐标分别是A(3,7),B(4,6),C(1,-2).则第四个顶点的坐标为( )
A.(0,-1) B.(6,15)C.(2,-3) D.(2,3)
5.平面直角坐标系中,从点A(1,1)出发,依次按向量a=(3,4),b=(2,-5),c=(3,1)移动,则终点坐标为________.
6.已知向量m=(1,2),写出一个与向量m方向相反的向量n=________.(用数字作答)
7.若向量a=(3,1),b=(7,-2),则与a-b共线的单位向量的坐标是________.
8.已知向量=(1,-3),=(-1,-2),=(2,4),则=________.
9.如图,已知平行四边形ABCD的三个顶点B、C、D的坐标分别是(-1,3)、(3,4)、(2,2),
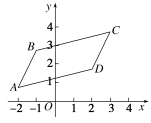
(1)求向量;
(2)求顶点A的坐标.
10.若向量=(3,-4),=(6,-3),=(5-m,-3-m),则点A,B,C能否构成三角形?若能,求出实数m满足的条件;若不能,请说明理由.
核心素养升级练
1.向量旋转具有反映点与点之间特殊对应关系的特征,在电子信息传导方面有重要应用.平面向量旋转公式在中学数学中用于求旋转相关点的轨迹方程具有明显优势,已知对任意平面向量=(x,y),把绕其起点沿逆时针方向旋转θ角得到向量=(x cos θ-y sin θ,x sin θ+y cos θ),叫做把点B绕点A沿逆时针方向旋转θ角得到点P.已知平面内点A(1,2),点B(1+,2-2),把点B绕点A沿顺时针方向旋转后得到点P,则点P的坐标为( )
A.(-2,1) B.(4,1)
C.(2,-1) D.(0,-1)
2.已知点A(-1,4),B(2,6),C(3,0),则满足++=0的G的坐标为________.
3.
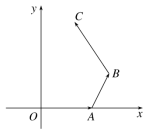
如图,已知O是平面直角坐标系的原点,∠OAB=∠ABC=120°,||=||=2||=4.
(1)求的坐标;
(2)若四边形ABCD为平行四边形,求点D的坐标.
6.3.2 平面向量的正交分解及坐标表示
6.3.3 平面向量加、减运算的坐标表示
必备知识基础练
1.答案:D
解析:因为a=(1,2),b=(3,4),所以a-b=(1,2)-(3,4)=(-2,-2).故选D.
2.答案:B
解析:由题意得,=(3,2)-(-2,3)=(5,-1).故选B.
3.答案:A
解析:∵=+,∴=+=(4,2)+(-1,-3)=(3,-1).故选A.
4.答案:B
解析:∵D为BC边的中点,A(-1,1),B(2,3),C(-6,5),∴D(-2,4),=(-1,3).故选B.
5.答案:B
解析:因为a+b=(-1,5),a-b=(5,-3),所以(a+b)-(a-b)=(-1,5)-(5,-3),即2b=(-6,8),所以b=(-3,4);故选B.
6.答案:AB
解析:因为a=(1,3),b=(-2,1),所以a+b=(-1,4),故A正确;a-b=(3,2),故B正确;b-a=(-3,-2),故C错误;-a-b=(1,-4),故D错误.故选AB.
7.答案:(-8,1)
解析:=-=(-5,-1)-(3,-2)=(-8,1).
8.答案:(4,6)
解析:设B点的坐标为(x,y),则=(x-3,y-4)=(1,2).∴解得,解得,∴B点的坐标是(4,6).
关键能力综合练
1.答案:A
解析:建立如下图所示的平面直角坐标系,设正方形网格的边长为1,
则a=(2,4),e1=(0,-2),e2=(1,0),

因为a=λ1e1+λ2e2=(λ2,-2λ1),所以,,可得,因此,λ1·λ2=-4.故选A.
2.答案:A
解析:∵=(3,-4),∴||=5,∴与向量的方向相反的单位向量为-=(-,).故选A.
3.答案:C
解析:在平行四边形ABCD中,=(2,4),=(1,3),所以=-=(-1,-1),所以=-=(2,4)-(-1,-1)=(3,5).故选C.
4.答案:ABC
解析:第四个顶点为D(x,y),当=时,(x-3,y-7)=(-3,-8),解得x=0,y=-1,此时第四个顶点的坐标为(0,-1);当=时,(x-3,y-7)=(3,8),解得x=6,y=15,此时第四个顶点的坐标为(6,15);当=时,(1,-1)=(x-1,y+2),解得x=2,y=-3,此时第四个顶点的坐标为(2,-3).∴第四个顶点的坐标为(0,-1)或(6,15)或(2,-3).故选ABC.
5.答案:(9,1)
解析:由题意,因为a=(3,4),b=(2,-5),c=(3,1),所以a+b+c=(8,0),所以从点A(1,1)出发,向右移动8个单位,终点坐标为(9,1).
6.答案:(-1,-2)(答案不唯一)
解析:由相反向量的定义可知,向量m=(1,2)的相反向量只要满足n=(λ,2λ)(λ<0)即可,当λ=-1时,n=(-1,-2).
7.答案:(-,)和(,-)
解析:因为a=(3,1),b=(7,-2),所以a-b=(-4,3),所以与a-b共线的单位向量的坐标为(-,)和(,-).
8.答案:(2,9)
解析:由题意,+==(1,-3)+(-1,-2)=(0,-5),又因为=(2,4),所以=-=(2,4)-(0,-5)=(2,9).
9.解析:(1)因为点B、C的坐标分别是(-1,3)、(3,4),
所以=(3,4)-(-1,3)=(4,1).
(2)设顶点A的坐标为(x,y),
因为四边形ABCD为平行四边形,D的坐标是(2,2),
所以=,即(4,1)=(2-x,2-y),
所以,解得,
所以顶点A的坐标为(-2,1).
10.解析:向量=(3,-4),=(6,-3),=(5-m,-3-m),
则=-=(3,1),=-=(2-m,1-m),
点A,B,C能构成三角形当且仅当与不共线,即有3(1-m)≠2-m,解得m≠,
所以当m≠时,点A,B,C能构成三角形.
核心素养升级练
1.答案:D
解析:由题意可知=(,-2),把点B绕点A逆时针方向旋转,得到点P,设P(x,y),则=(cos +2sin ,sin -2cos )=(-1,-3),所以,解得,所以点P的坐标为(0,-1),故选D.
2.答案:(,)
解析:设G的坐标为(x,y),且A(-1,4),B(2,6),C(3,0),因为++=0,可得(-1-x,4-y)+(2-x,6-y)+(3-x,-y)=(0,0),可得x==,y==,所以G的坐标为(,).
3.解析:(1)过点B作BE垂直x轴于点E,如图所示:
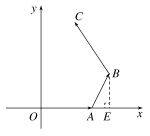
因为∠OAB=120°,所以∠EAB=60°,
又||=2,所以在Rt△ABE中,AE=1,BE=,
又||=4,所以A(4,0),B(5,),
所以=(1,).
(2)过点C作CF垂直x轴于点F,过点B作BM垂直CF轴于点M,过点A作AN垂直BM轴于点N,如图所示:

在Rt△CMB中,||=4,∠CBM=60°,所以BM=2,CM=2,
在Rt△ANB中,||=2,∠ABN=60°,
所以BN=1,AN=,即MN=AF=1,MF=,
所以CF=3,OF=3,即C(3,3),
设点D(x,y),因为四边形ABCD为平行四边形,所以=,
又=(1,),=(3-x,3-y),
所以,解得,
所以点D坐标为(2,2).
人教A版 (2019)必修 第二册第六章 平面向量及其应用6.3 平面向量基本定理及坐标表示课后复习题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000292_t7/?tag_id=28" target="_blank">第六章 平面向量及其应用6.3 平面向量基本定理及坐标表示课后复习题</a>,共4页。试卷主要包含了选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
高中人教A版 (2019)6.3 平面向量基本定理及坐标表示免费复习练习题: 这是一份高中人教A版 (2019)<a href="/sx/tb_c4000292_t7/?tag_id=28" target="_blank">6.3 平面向量基本定理及坐标表示免费复习练习题</a>,共5页。
高中数学人教A版 (2019)必修 第二册第六章 平面向量及其应用6.3 平面向量基本定理及坐标表示同步达标检测题: 这是一份高中数学人教A版 (2019)必修 第二册第六章 平面向量及其应用6.3 平面向量基本定理及坐标表示同步达标检测题,共7页。试卷主要包含了已知向量a=,b=,则a-b=等内容,欢迎下载使用。













