辽宁省葫芦岛市建昌县2022-2023学年七年级下学期期末数学试题（含答案）

2022-2023学年度下学期七年级期末检测

数学试题

考试时间120分钟试卷满分120分

考生注意：请在答题卡各题目规定区域内作答，答在本试卷上无效.

第一部分选择题（共20分）

一、选择题（本大题共10个小题，每小题2分，共20分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.下列四个图案中，能用平移来分析其形成过程的是（）

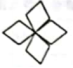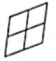A. B. C. D.

2.下面调查中，适合采用全面调查的是（）

A.调查某批次汽车的抗撞击能力 B.乘飞机时对乘客进行安全检查

C.调查全国中学生喜爱的电视节目 D.调查某品牌饮料的含糖量

3.下列各实数是无理数的是（）

A. B. C.9.090090009 D.

4.不等式组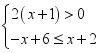的解集在数轴上表示正确的是（）

A. B. C. D.

5.已知点P在x轴上，位于原点左侧，到原点的距离为3个单位长度，则点P的坐标是（）

A. B. C. D.

6.如图所示，已知，，则的度数是（）

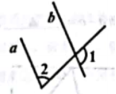
A.70° B.100° C.110° D. 120°

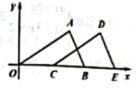
7.如图，在平面直角坐标系中，将水平向右平移得到，已知，，则点D的坐标为（）

A. B. C. D.

8.下列说法正确的是（）

A.在同一平面内，若，，则

B.若，则

C.已知点M到直线l的距离为5cm，点N为直线l上一动点，则MN长可能为4cm

D.一组数据共有100个，分为若干组，其中一组的频率为0.4，则这组的频数是40

9.我国古代数学著作《九章算术》记载一道问题：“今有五雀，六燕，集称之衡，雀俱重，燕俱轻；一雀一燕交而处，衡适平；并燕、雀重一斤，问燕雀一枚各重几何？”其大意是：“现在有5只雀，6只燕，分别集中放在天平上称重，聚在一起的雀重燕轻；将一只雀一只燕交换位置而放，重量相等；5只雀、6只燕重量共一斤，问雀和燕各重多少？”古代记1斤为16两，设1只雀x两，一只燕y两，可列方程组为（）

A. B. C. D.

10.如图，将一个含30°角的直角三角板的直角顶点C放在直尺的两边MN，PQ之间，则下列结论中：①；②：；③；④若.则.其中正确结论的个数是（）

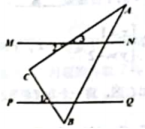
A.1个 B.2个 C.3个 D.4个

第二部分非选择题（共100分）

二、填空题（本题共6个小题，每小题3分，共18分）

11.的平方根是______.

12.若是关于x，y的二元一次方程组的解，则______.

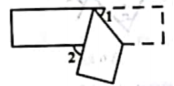
13.如右图，将一个宽度相等的纸条按如图所示方法折叠，若，则______.

14.根据如下图所示统计图回答问题：

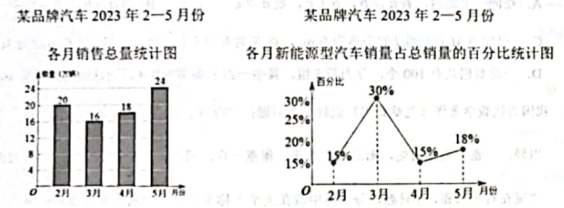
该品牌汽车在2023年2—5月份新能源型汽车销量最多月份的销量是______万辆.

15.在平面直角坐标系中，有A，B，C三点，，，，己知轴，当BC取得最小值时点C的坐标为______.

16.对于不等式组，以下结论中：①若，则不等式组的解集为；②若，则不等式组无解；③若不等式组无解，则；④若不等式组只有一个整数解，则.其中正确的结论是：______（将正确结论的序号填在横线上）.

三、解答题（第17题6分，第18，19小题各8分，共22分）

17.计算：

18.已知，在等式中，当时，；当时，.求时y的值.

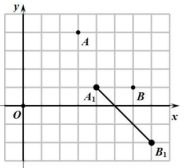
19.如图，在平面直角坐标系中，每个小方格都是边长为1个单位长的正方形，A，B，O三点均在格点上.

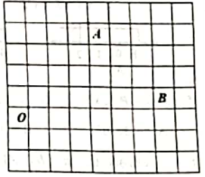
（1）请画出以点O为坐标原点建立的平面直角坐标系，井直接写出点B的坐标.

（2）将线段AB向右平移1个单位，再向下平移3个单位，得到线段，画出线段；若点在线段AB上，直接写出平移后点P的对应点的坐标（用含m，n的式子表示）；

（3）连接，，则四边形的面积为______.

四、解答题（第20题8分，第21题8分，共16分）

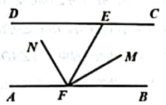
20.如图，，点E，F为CD，AB上两点，.FM平分，.求的度数.

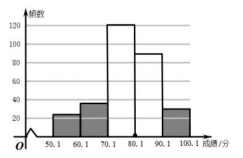
21.为评估全县七年级学生体质健康状况，评估小组从七年级5000名学生中抽取部分同学的成绩（成绩均为正整数，满分为100分）进行统计分析，绘制如下所示的频数分布表及不完整的频数分布直方图：

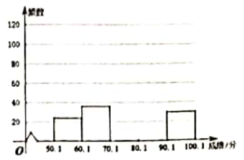
请根据尚未完成的表格，解答下列问题：

（1）本次抽样调查的样本容量为______，表中______；

（2）补全如图所示的频数分布直方图；

（3）若用扇形统计图表示各分数段所占的百分比，则“80.1—90.1”分数段所占区域圆心角的度数为______；

（4）若成绩为80分以上（不含80分）的同学成绩为优秀，估计该校七年级同学中成绩优秀的学生有______人.

五、解答题（本题10分）

22.阅读材料：

李老师给数学兴趣小组布置了这样一个关于不等式的问题：求不等式的解集.

小组成员百思不得其解，这时，李老师提示说：“我们可以利用有理数的运算法则解决这一问题”，话音刚落，聪明的小明就说：“我明白了”！你们想到解决问题的方法了吗？小明是这样做的：根据有理数的乘法法则“两数相乘，同号得正，异号得负，并把绝对值相乘”.

可得①；或②，

解不等式组①得：，解不等式组②得：，

∴原不等式的解集为：或.

你明白了吗？请结合以上材料解答问题：解不等式.

六、解答题（满分10分）

23.如图，在平面直角坐标系中，，点在x轴的负半轴上，点C在第二象限，轴，且，点在第一象限.

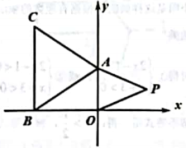
（1）求B，C两点的坐标；

（2）是否存在m，使以A，B，O，P为顶点的四边形的面积等于？若存在，求出点P的坐标，若不存在，请说明理由.

七、解答题（满分12分）

24.多功能家庭早餐机可以制作多种口味的美食，深受消费者的喜爱.某商场经营A，B两种型号的家庭早餐机，在新品上市促销活动中，连续两天的销售情况如表所示：

（1）每台A型早餐机和每台B型早餐机的价格分别是多少元；

（2）某商家计划购进A，B两种型号早餐机共20台，但总费用不超过2200元，那么至少要购进A型早餐机多少台.

八、解答题（本题12分）

25.如图，已知，点C为射线AP上的一个动点，连接BC，BD平分交射线AP于点D，BE平分交射线AP于点E.

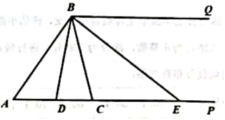
（1）请直接写出与之间的数量关系；

（2）在点C运动的过程中，当时，求与的数量关系；

（3）在点C运动的过程中，直接写出与的数量关系.

2022—2023学年度下学期七年级期中检测

数学试题参考答案及评分标准

（※若有其他正确解法或证法请参照此标准赋分）

一、选择题（本大题共10个小题，每小题2分，共20分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

二、填空题（本题共6个小题，每小题3分，共18分.）

11.12.13.74°14.4.815.16.①②

三、解答题（第17题6分，第18，19小题各8分，共22分）

17.解：原式……………………………………2分

…………………………………………………………4分

……………………………………………………………………6分

18.解：根据题意可得：

……………………………………………………………………………3分

解得：………………………………………………………………………………5分

……………………………………………………………………………6分

当时，…………………………………………………………8分

19.（1）如图所示，.…………………………………………………………………3分

（2）如图所示，.……………………………………………………………6分

（3）6…………………………………………………………………………………………8分

四、解答题（第20题8分，第21题各8分，共16分）

20.证明：

……………………………………………………………………2分

……………………………………………3分

平分

…………………………………………………………………4分

………………………………………………………………………………5分

………………………………………………6分

…………………………………………8分

21.（1）30010％…………………………………………………………………………2分

（2）如图所示…………………………………………………………………………………4分

（3）108°………………………………………………………………………………………6分

（4）2000………………………………………………………………………………………8分

五、解答题（本题10分）

22.根据题意可得：

①；②………………………………………………………………4分

解不等式组①，无解………………………………………………………………………6分

解不等式组②，………………………………………………………………8分

原不等式的解集为…………………………………………………………10分

六、解答题（满分10分）

23.解：（1）：点在x轴的负半轴上

………………………………………………………………………………2分

解得或（不符合题意，舍去）

………………………………………………………………………………4分

又点C在第二象限，轴，且

………………………………………………………………………………6分

（2）存在，当点时，

即，

…………………………………………………………………………………10分

七、解答题（满分12分）

24，（1）解：设每台A型早餐机x元，每台B型早餐机y元，根据题意可得……1分

…………………………………………………………………………3分

解得：…………………………………………………………………………5分

答：每台A型早餐机80元，每台B型早餐机120元…………………………………6分

（2）解：设购进A型早餐机m台，则购进B型早餐机台，根据题意可得…7分

………………………………………………………………9分

解得：………………………………………………………………………………11分

答：至少购进A型早餐机5台……………………………………………………………12分

八、解答题（满分12分）

25.（1）…………………………………………………………2分

（2）

，……………………………………………4分

…………………………………………………………………………5分

…………………………………………………………………………6分

平分

平分

……………………………………………………………………………8分

…………………………………………………………………………10分

（3）…………………………………………………………………12分