高考物理复习 计算题专练 电磁感应（含答案解析）

这是一份高考物理复习 计算题专练 电磁感应（含答案解析），共16页。试卷主要包含了完成下列问题，5－3，4 m/s，vC′=3等内容，欢迎下载使用。
2020(人教版)高考物理复习 计算题专练 电磁感应1.如图甲所示，MN、PQ两条平行的光滑金属轨道与水平面成θ=37°角固定，M、P之间接电阻箱R，导轨所在空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度B=1 T．质量为m的金属杆ab水平放置在轨道上，其接入电路的电阻值为r.现从静止释放杆ab，测得最大速度为vm.改变电阻箱的阻值R，得到vm与R的关系如图乙所示．已知导轨间距L=2 m，重力加速度g取10 m/s2，轨道足够长且电阻不计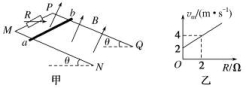．(1)杆ab下滑过程中，判断感应电流的方向．(2)求R=0时，闭合电路中的感应电动势E的最大值．(3)求金属杆的质量m和阻值r.             2.边长为L的正方形区域内有垂直纸面向里的匀强磁场，穿过该区域的磁通量随时间变化的图象如图甲所示．将边长为，总电阻为R的正方形线圈abcd放入磁场，线圈所在平面与磁感线垂直，如图乙所示．求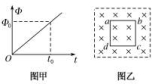：(1)磁感应强度的变化率；(2)t0时刻线圈ab边受到的安培力大小．         3.轻质细线吊着一质量为m=0.42 kg、边长为l=1 m、匝数n=10的正方形线圈,其总电阻为r=1 Ω。在线圈的中间位置以下区域分布着磁场,如图甲所示。磁场方向垂直纸面向里,磁感应强度大小随时间变化关系如图乙所示,整个过程线圈不翻转,重力加速度g取10 m/s2。(1)判断线圈中产生的感应电流的方向是顺时针还是逆时针;(2)求线圈的电功率;(3)求在t=4 s时轻质细线上的拉力大小。         4.如图甲所示,在水平面内的直角坐标系的第一象限有磁场分布,方向垂直于水平面向下,磁感应强度沿y轴方向没有变化,沿x轴方向B与x成反比,如图乙所示。顶角θ=45°的光滑金属长导轨MON固定在水平面内,ON与x轴重合,一根与ON垂直的长导体棒在水平向右的外力作用下沿导轨向右滑动,导体棒在滑动过程中始终与导轨接触,且与x轴垂直。已知t=0时,导体棒位于顶点O处,导体棒的质量为m=1 kg,回路接触点总电阻恒为R=0.5 Ω,其余电阻不计。回路电流I与时间t的关系如图丙所示,图线是过原点的直线。求: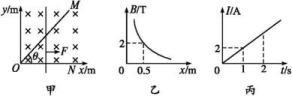(1)t=2 s时回路的电动势E;(2)0~2 s时间内流过回路的电荷量q和导体棒的位移x1;(3)导体棒滑动过程中水平外力F的瞬时功率P(单位:W)与横坐标x(单位:m)的关系式。         5.如图所示,粗糙斜面的倾角θ=37°,半径r=0.5 m的圆形区域内存在着垂直于斜面向下的匀强磁场。一个匝数n=10的刚性正方形线框abcd通过松弛的柔软导线与一个额定功率P=1.25 W的小灯泡L相连,圆形磁场的一条直径恰好过线框bc边。已知线框质量m=2 kg,总电阻R0=1.25 Ω,边长l>2r,与斜面间的动摩擦因数μ=0.5。从t=0时起,磁场的磁感应强度按B=2-t(T)的规律变化。开始时线框静止在斜面上,在线框运动前,灯泡始终正常发光。设最大静摩擦力等于滑动摩擦力,g取10 m/s2,sin 37°=0.6,cos 37°=0.8。求: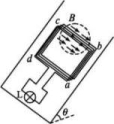(1)线框不动时,回路中的感应电动势E;(2)小灯泡正常发光时的电阻R;(3)线框保持不动的时间内,小灯泡产生的热量Q。       6.如图所示，足够长的光滑导轨ab、cd固定在竖直平面内，导轨间距为l，b、c两点间接一阻值为R的电阻．ef是一水平放置的导体杆，其质量为m、有效电阻值为R，杆与ab、cd保持良好接触．整个装置放在磁感应强度大小为B的匀强磁场中，磁场方向与导轨平面垂直．现用一竖直向上的力拉导体杆，使导体杆从静止开始做加速度为的匀加速运动，上升了h高度，这一过程中b、c间电阻R产生的焦耳热为Q，g为重力加速度，不计导轨电阻及感应电流间的相互作用．求：(1)导体杆上升h高度过程中通过杆的电荷量；(2)导体杆上升h高度时所受拉力F的大小；(3)导体杆上升h高度过程中拉力做的功．        7.如图所示，MN、PQ是两条水平、平行放置的光滑金属导轨，导轨的右端接理想变压器的原线圈，变压器的副线圈与电阻R=20 Ω组成闭合回路，变压器的原副线圈匝数之比n1：n2=1：10，导轨宽L=5 m．质量m=2 kg、电阻不计的导体棒ab垂直MN、PQ放在导轨上，在水平外力F作用下，从t=0时刻开始在图示的两虚线范围内往复运动，其速度随时间变化的规律是v=2sin20πt(m/s)．垂直轨道平面的匀强磁场的磁感应强度B=4 T．导轨、导线和线圈电阻均不计．求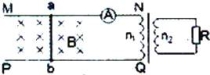：(1)ab棒中产生的电动势的表达式；ab棒中产生的是什么电流？(2)电阻R上的电热功率P.(3)从t=0到t1=0.025 s的时间内，外力F所做的功．           8.如图所示，匀强磁场的磁感应强度方向垂直纸面向里，宽度为l，上、下边界与地面平行，下边界与地面相距l.将一个边长为l，质量为m，总电阻为R的正方形刚性导电线框ABCD置于匀强磁场区域上方，线框CD边与磁场上边界平行，从高于磁场上边界h的位置由静止释放，h的值能保证AB边匀速通过磁场区域．从AB边离开磁场到CD边落到地面所用时间是AB边通过磁场时间的2倍(重力加速度为g)．求：(1)线框通过磁场过程中电流的方向；(2)磁场区域内磁感应强度的大小；(3)CD边刚进入磁场时线框加速度与h的函数关系，分析h在不同情况下加速度的大小和方向，计算线框通过磁场区域产生的热量．       9.半径分别为r和2r的同心圆形导轨固定在同一水平面内，一长为r、质量为m且质量分布均匀的直导体棒AB置于圆导轨上面．BA的延长线通过圆导轨中心O，装置的俯视图如图所示．整个装置位于一匀强磁场中，磁感应强度的大小为B，方向竖直向下．在内圆导轨的C点和外圆导轨的D点之间接有一阻值为R的电阻(图中未画出)．直导体棒在水平外力作用下以角速度ω绕O逆时针匀速转动，在转动过程中始终与导轨保持良好接触．设导体棒与导轨之间的动摩擦因数为μ，导体棒和导轨的电阻均可忽略．重力加速度大小为g.求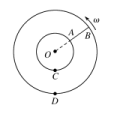：(1)通过电阻R的感应电流的方向和大小；(2)外力的功率．         10.如图所示,光滑的定滑轮上绕有轻质柔软细线,线的一端系一质量为2m的重物,另一端系一质量为m、电阻为R的金属杆。在竖直平面内有间距为l的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值也为R的电阻,其余电阻不计,磁感应强度为B0的匀强磁场与导轨平面垂直,开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降。运动过程中金属杆始终与导轨垂直且接触良好,不计一切摩擦和接触电阻,重力加速度为g。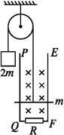(1)求重物匀速下降的速度v。(2)求重物从释放到下降h的过程中,电阻R中产生的热量QR。(3)将重物下降h时的时刻记作t=0,速度记为v0,若从t=0开始磁感应强度逐渐减小,且金属杆中始终不产生感应电流,写出磁感应强度的大小Bt随时间t变化的关系。       11.两根足够长的平行金属导轨间的距离为L，导轨光滑且电阻不计，导轨所在的平面与水平面夹角为θ.在导轨所在平面内，分布磁感应强度为B、方向垂直于导轨所在平面的匀强磁场．把一个质量为m的导体棒ab放在金属导轨上，在外力作用下保持静止，导体棒与金属导轨垂直且接触良好，与金属导轨接触的两点间的导体棒电阻为R1.完成下列问题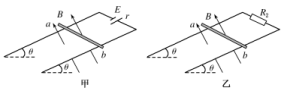：(1)如图甲，金属导轨的一端接一个内阻为r的直流电源，撤去外力后导体棒仍能静止，求直流电源的电动势；(2)如图乙，金属导轨的一端接一个阻值为R2的定值电阻，撤去外力让导体棒由静止开始下滑，在加速下滑的过程中，当导体棒的速度达到v时，求此时导体棒的加速度；(3)求第(2)问中导体棒所能达到的最大速度．            12.如图甲所示，匀强磁场的磁感应强度B为0.5 T，其方向垂直于倾角θ为30°的斜面向上．绝缘斜面上固定有“∧”形状的光滑金属导轨MPN(电阻忽略不计)，MP和NP长度均为2.5 m，MN连线水平，长为3 m．以MN中点O为原点，OP为x轴建立一维坐标系Ox.一根粗细均匀的金属杆CD，长度d为3 m，质量m为1 kg，电阻R为0.3 Ω，在拉力F的作用下，从MN处以恒定速度v=1 m/s在导轨上沿x轴正向运动(金属杆与导轨接触良好)．g取10 m/s2.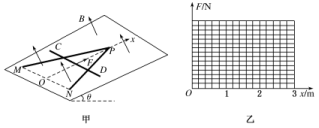(1)求金属杆CD运动过程中产生的感应电动势E及运动到x=0.8 m处电势差UCD；(2)推导金属杆CD从MN处运动到P点过程中拉力F与位置坐标x的关系式，并在图乙中画出F－x关系图象；(3)求金属杆CD从MN处运动到P点的全过程产生的焦耳热．         13.如图所示,宽度为l的平行光滑的金属轨道,左端为半径为r1的四分之一圆弧轨道,右端为半径为r2的半圆轨道,中部为与它们相切的水平轨道。水平轨道所在的区域有磁感应强度为B的竖直向上的匀强磁场。一根质量为m的金属杆a置于水平轨道上,另一根质量为m0的金属杆b由静止开始自左端轨道最高点滑下,当b滑入水平轨道某位置时,a就滑上了右端半圆轨道最高点(b始终运动且a、b未相撞),并且a在最高点对轨道的压力大小为mg,此过程中通过a的电荷量为q,a、b棒的电阻分别为R1、R2,其余部分电阻不计。在b由静止释放到a运动到右端半圆轨道最高点过程中。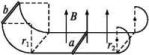(1)在水平轨道上运动时b的最大加速度是多大?(2)自b释放到a到达右端半圆轨道最高点过程中系统产生的焦耳热是多少?(3)在a刚到达右端半圆轨道最低点时b的速度是多大?          14.如图所示，两根足够长且平行的光滑金属导轨与水平面成53°角固定放置，导轨间连接一阻值为6 Ω的电阻R，导轨电阻忽略不计．在两平行虚线m、n间有一与导轨所在平面垂直、磁感应强度为B的匀强磁场．导体棒a的质量为ma=0.4 kg，电阻Ra=3 Ω；导体棒b的质量为mb=0.1 kg，电阻Rb=6 Ω；它们分别垂直导轨放置并始终与导轨接触良好．a、b从开始相距L0=0.5 m处同时由静止开始释放，运动过程中它们都能匀速穿过磁场区域，当b刚穿出磁场时，a正好进入磁场(g取10 m/s2，不计a、b之间电流的相互作用)．求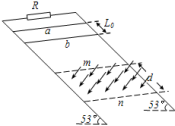：(1)当a、b分别穿越磁场的过程中，通过R的电荷量之比；(2)在穿越磁场的过程中，a、b两导体棒匀速运动的速度大小之比；(3)磁场区域沿导轨方向的宽度d；(4)在整个过程中产生的总焦耳热．       15.如图所示，两根质量均为m=2 kg的金属棒垂直放在光滑的水平导轨上，左右两部分导轨间距之比为12，导轨间有大小相等但左、右两部分方向相反的匀强磁场，两棒电阻与棒长成正比，不计导轨电阻．现用250 N的水平拉力F向右拉CD棒，CD棒运动x=0.5 m时其上产生的焦耳热为Q2=30 J，此时两棒速率之比为vA：vC=1：2，现立即撤去拉力F，设导轨足够长且两棒始终在不同磁场中运动，求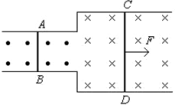：(1)在CD棒运动0.5 m的过程中，AB棒上产生的焦耳热；(2)撤去拉力F瞬间，两棒的速度大小vA和vC；(3)撤去拉力F后，两棒最终匀速运动的速度大小v′A和v′C.                  
答案解析1.解：(1)由右手定则可知，电流方向为b→a(或aMPba)．(2)由题图可知，当R=0时，杆的速度稳定后，它以2 m/s的速度匀速下滑，此时电路中的感应电动势最大，最大值E=BLv=4 V.(3)金属杆下滑的最大速度即为vm.杆切割磁感线产生的感应电动势的最大值E=BLvm由闭合电路的欧姆定律得I=杆达到最大速度时，满足条件mgsinθ－BIL=0解得vm=(R＋r)结合图象可得=k，k=1 m/(s·Ω)r=2 m/s解得m= kg，r=2 Ω.  2.解：(1)由题意可知Φ0=B0L2，=，解得=(2)线圈中的感应电动势为E=2×=由闭合电路欧姆定律I=，安培力F=解得F=  3.解：(1)由楞次定律知感应电流的方向为逆时针方向。(2)由法拉第电磁感应定律得E=n=n·l2=0.5V则P==0.25W。(3)I==0.5AF安=nBIl,方向向上,当t=4s时,磁感应强度B=0.6T则F安+F拉=mg联立解得F拉=1.2N。  4.解：(1)根据I-t图像可知,I=k1t(k1=2A/s)则当t=2s时,回路电流I1=4A根据闭合电路欧姆定律可得E=I1R=2V。(2)流过回路的电荷量q=t由I-t图像可知,0~2s内的平均电流=2A,得q=4C由欧姆定律得I=,l=xtan45°根据B-x图像可知,B=(k2=1T·m)联立解得v=t由于=1m/s2,再根据v=v0+at,可知a=1m/s2则导体棒做匀加速直线运动所以0~2s时间内导体棒的位移x1=at2=2m。(3)导体棒受到的安培力F安=BIl根据牛顿第二定律有F-F安=ma又2ax=v2P=Fv解得P==4x+(各物理量均取国际单位制中的单位)。  5.解：(1)由法拉第电磁感应定律有E=n=nπr2=10×π×0.52V=2.5V。(2)小灯泡正常发光,有P=I2R由闭合电路欧姆定律有E=I(R0+R)即P=R代入数据解得R=1.25Ω。(3)当线框恰好要运动时,设磁场的磁感应强度大小为B',对线框bc边在磁场中的部分受力分析。安培力F安=nB'I×2r=nB'×2r由共点力的平衡条件有mgsinθ=F安+Ff=2nB'r·+μmgcosθ解得线框刚要运动时,磁场的磁感应强度大小B'=0.4T得线框在斜面上可保持静止的时间t=s小灯泡产生的热量Q=Pt=1.25×J≈3.14J。  6.解：(1)通过杆的电荷量q=IΔt，根据闭合电路欧姆定律有I=，根据法拉第电磁感应定律得E=，联立以上各式解得q==.(2)设导体杆上升h高度时速度为v1、拉力为F，根据运动学公式得v1= =，根据牛顿第二定律得F－mg－BI1l=ma=m，根据闭合电路欧姆定律得I1=，联立以上各式解得F=＋.(3)由功能关系得WF－mgh－2Q=mv－0，解得WF=＋2Q.  7.解：(1)ab棒中产生的电动势的表达式为E=BLv=40sin20πt(V)故ab棒中产生的是正弦式交变电流．(2)设原线圈上电压的有效值为U1，则U1==20 V设副线圈上电压的有效值为U2，则=解得U2=200 V电阻R上的电热功率P==4×103 W(3)由以上分析可知，该正弦交流电的周期T==0.1 s．从t=0到t1=0.025 s，经历了四分之一个周期．设在这段时间内电阻R上产生的热量为Q，则Q=·=100 J在t1=0.025 s时刻，ab棒的速度为v，则v=2sin20πt1=2 m/s由能量守恒定律可得这段时间内外力F做的功W=Q＋mv2=104 J  8.解：(1)由楞次定律得，线框中电流方向：CD边在磁场中时沿D→C→B→A→D方向AB边在磁场中时沿A→B→C→D→A方向(2)设线框AB边在磁场中做匀速运动的速度大小为v1，穿过磁场的时间为t，AB边切割磁感线产生的电动势为E1，线框中电流为I1，则mg=BI1lE1=Blv1I1=l=v1t根据题意和匀变速直线运动规律，得l－l=v1(2t)＋g(2t)2联立解得v1=2，B=(3)设线框CD边刚进入磁场时，速度大小为v，加速度大小为a，线框CD边产生的电动势为E，电流为I，线框通过磁场区域产生的热量为Q由动能定理得mgh=mv2－0解得v=E=BlvI=解得I=由牛顿第二定律得mg－BIl=ma解得a=g当h=2l时，a=0当h>2l时，加速度大小为g，方向竖直向上当h<2l时，加速度大小为g，方向竖直向下根据能量守恒定律，有Q=mg(h＋2l)－mv解得Q=mgh.  9.解：(1)在Δt时间内，导体棒扫过的面积为ΔS=ωΔt[(2r)2－r2]①根据法拉第电磁感应定律，导体棒上感应电动势的大小为E=②根据右手定则，感应电流的方向是从B端流向A端．因此，通过电阻R的感应电流的方向是从C端流向D端．由欧姆定律可知，通过电阻R的感应电流的大小I满足I=③联立①②③式得I=④(2)在竖直方向有mg－2N=0⑤式中，由于质量分布均匀，内、外圆导轨对导体棒的支持力大小相等，其值为N.两导轨对运行的导体棒的滑动摩擦力均为f=μN⑥在Δt时间内，导体棒在内、外圆导轨上扫过的弧长分别为l1=rωΔt⑦l2=2rωΔt⑧克服摩擦力做的总功为Wf=f(l1＋l2)⑨在Δt时间内，消耗在电阻R上的功为WR=I2RΔt⑩根据能量守恒定律知，外力在Δt时间内做的功为W=Wf＋WR⑪外力的功率为P=⑫由④至⑫式得P=μmgωr＋.  10.解：(1)重物匀速下降时,设细线对金属棒的拉力为FT,金属棒所受安培力为F。由平衡条件FT=mg+F。由安培力公式得F=B0Il。由闭合电路欧姆定律得I=。由法拉第电磁感应定律得E=B0lv。对重物,由平衡条件得FT=2mg。由上述式子解得v=。(2)设电路中产生的总热量为Q,则由系统功能关系得2mgh-mgh=(2m)v2+mv2+Q。电阻R中产生的热量为QR,由串联电路特点QR=Q。所以QR=mgh-。(3)金属杆中恰好不产生感应电流,即磁通量不变Φ0=Φt,所以B0hl=Bt(h+h2)l。式中h2=v0t+at2。由牛顿第二定律得对系统a=。则磁感应强度与时间t的关系为Bt=。  11.解：(1)回路中的电流为I=，导体棒受到的安培力为F安=BIL，对导体棒受力分析知F安=mgsinθ.联立上面三式解得E=.(2)当导体棒速度为v时，产生的感应电动势E=BLv，此时电路中电流I==，导体棒受到的安培力F=BIL=.根据牛顿第二定律有ma=mgsinθ－，解得a=gsinθ－.(3)当=mgsinθ时，导体棒达到最大速度vm，可得vm=.  12.解：(1)金属杆CD在匀速运动中产生的感应电动势E=Blv(l=d)，代入数值得E=1.5 V.当x=0.8 m时，金属杆在导轨间的电势差为零(被短路)，设此时杆在导轨外的长度为l外，则l外=d－d，OP= ，得l外=1.2 m.由楞次定律判断D点电势高，故CD两端电势差UCD=－Bl外v=－0.6 V.(2)杆在导轨间的长度l与位置x的关系是l=d=3－x，对应的电阻R1=R，电流I=，杆受到的安培力F安=BIl=7.5－3.75x，根据平衡条件得F=F安＋mgsinθ，得F=12.5－3.75x(N)(0≤x≤2)，画出的F—x图象如图所示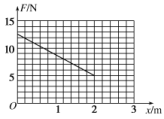．(3)外力F所做的功WF等于F—x图线与x轴所围成的图形的面积，即WF=×2 J=17.5 J.而杆的重力势能增加量ΔEp=mgsinθ，故全过程产生的焦耳热Q=WF－ΔEp=7.5 J.  13.解：(1)设杆b刚刚滑到左端轨道最低端时的速度为vb1,由机械能守恒定律,m0=m0gr1,所以vb1=b刚滑到水平轨道时加速度最大,则E=Blvb1,I=,根据牛顿第二定律有,F安=BIl=m0a得杆b的最大加速度a=。(2)设杆a到达右端半圆轨道最高点时,杆a的速度为va1,杆b的速度为vb2,根据动量定理有-BIlt=m0vb2-m0vb1,即-Blq=m0vb2-m0vb1所以vb2=根据牛顿第二定律和第三定律,得2mg=m所以va1=因为m0gr1=m0+mg2r2+Q所以系统产生的焦耳热Q=Blq-3mgr2-。(3)根据能量守恒,有2mgr2=所以杆a刚到达水平轨道右端时的速度va2=在杆b和杆a在水平轨道上运动时,符合动量守恒条件,根据动量守恒定律,有m0vb1=m0vb3+mva2杆a刚到达水平轨道最右端时,杆b的速度vb3=。  14.解：(1)由法拉第电磁感应定律得=，平均电流=，通过导体棒的总电荷量q总=Δt=.在b穿越磁场的过程中，b是电源，a与R是外电路，电路的总电阻R总1=Rb＋=8 Ω.则通过R的电荷量为qRb=q总=·.同理，a穿越磁场的过程中，R总2=Ra＋=6 Ω，通过R的电荷量为qRa=q总=·.解得qRa：qRb=2：1.(2)设b在磁场中匀速运动的速度大小为vb，则b中的电流Ib=.由平衡条件得=magsin53°.同理，a在磁场中匀速运动时有=magsin53°.联立可得va：vb=3：1.(3)设a、b穿越磁场的过程中的速度分别为va和vb.由题意得va=vb＋gtsin53°，d=vbt，因v－v=2gL0sin53°，解得d=0.25 m.(4)由F安a=magsin53°，故Wa=magdsin53°=0.8 J.同理Wb=mbgdsin53°=0.2 J.在整个过程中，电路中共产生焦耳热为Q=Wa＋Wb=1 J.  15.解：(1)设两棒的长度分别为l和2l，所以电阻分别为R和2R，由于电路中任何时刻电流均相等，根据焦耳定律Q=I2Rt可知AB棒上产生的焦耳热Q1=15 J.(2)根据能量守恒定律，有Fx=mv＋mv＋Q1＋Q2又vAvC=12，联立以上两式并代入数据得vA=4 m/s，vC=8 m/s.(3)撤去拉力F后，AB棒继续向左做加速运动，而CD棒向右做减速运动，两棒最终匀速运动时电路中电流为零，即两棒切割磁感线产生的电动势大小相等，此时两棒的速度满足BLvA′=B·2LvC′即vA′=2vC′(不对过程进行分析，认为系统动量守恒是常见错误)对两棒分别应用动量定理，规定水平向左为正方向，有FA·t=mvA′－mvA，－FC·t=mvC′－mvC.因为FC=2FA，故有=联立以上各式解得vA′=6.4 m/s，vC′=3.2 m/s.