
2022-2023学年四川省达州市达川区七年级(下)期末数学试卷(含解析)
展开1. 下列图形中,不是轴对称图形的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. a2÷a2=a3B. (−a2)3=a6C. a2⋅a3=a6D. (3a)2=9a2
3. 下列事件为必然事件的是( )
A. 一名射击运动员射击一次,中靶
B. 彩票的中奖率是15%,那么买100张彩票必有15张中奖
C. 掷一枚质地均匀的骰子,掷出的点数是质数
D. 一个三角形,其任意两边之和大于第三边
4. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
下列说法正确的是( )
A. 当h=70cm时,t=1.50s
B. 随着h逐渐升高,t也逐渐变大
C. h每增加10cm,t减小1.23s
D. 随着h逐渐升高,小车下滑的平均速度逐渐加快
5. 如图,直线m、n被直线a、b所截,下列条件中,不能判断直线m//n的是( )
A. ∠2=∠5
B. ∠3+∠4=180°
C. ∠3=∠5
D. ∠1=∠6
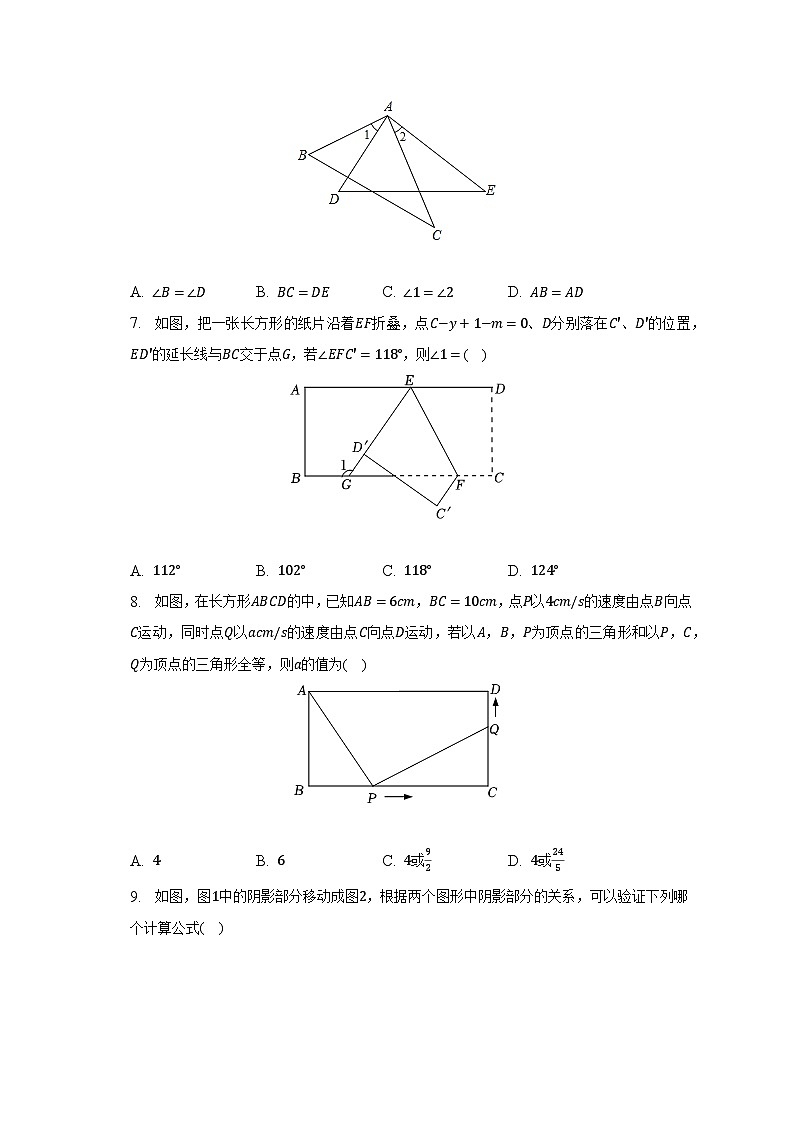
6. 如图,已知AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌△ADE的是( )
A. ∠B=∠DB. BC=DEC. ∠1=∠2D. AB=AD
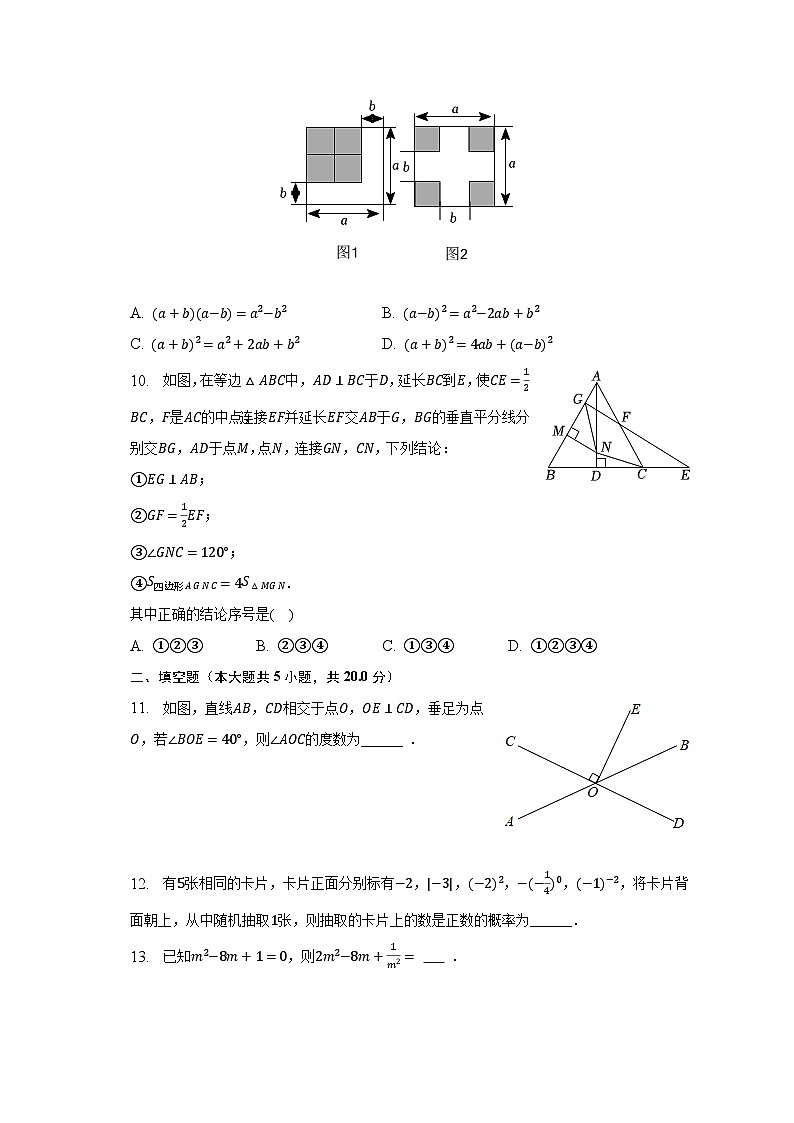
7. 如图,把一张长方形的纸片沿着EF折叠,点C−y+1−m=0、D分别落在C′、D′的位置,ED′的延长线与BC交于点G,若∠EFC′=118°,则∠1=( )
A. 112°B. 102°C. 118°D. 124°
8. 如图,在长方形ABCD的中,已知AB=6cm,BC=10cm,点P以4cm/s的速度由点B向点C运动,同时点Q以acm/s的速度由点C向点D运动,若以A,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,则a的值为( )
A. 4B. 6C. 4或92D. 4或245
9. 如图,图1中的阴影部分移动成图2,根据两个图形中阴影部分的关系,可以验证下列哪个计算公式( )
A. (a+b)(a−b)=a2−b2B. (a−b)2=a2−2ab+b2
C. (a+b)2=a2+2ab+b2D. (a+b)2=4ab+(a−b)2
10. 如图,在等边△ABC中,AD⊥BC于D,延长BC到E,使CE=12BC,F是AC的中点,连接EF并延长EF交AB于G,BG的垂直平分线分别交BG,AD于点M,点N,连接GN,CN,下列结论:
①EG⊥AB;
②GF=12EF;
③∠GNC=120°;
④S四边形AGNC=4S△MGN.
其中正确的结论序号是( )
A. ①②③B. ②③④C. ①③④D. ①②③④
二、填空题(本大题共5小题,共20.0分)
11. 如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠BOE=40°,则∠AOC的度数为______ .
12. 有5张相同的卡片,卡片正面分别标有−2,|−3|,(−2)2,−(−14)0,(−1)−2,将卡片背面朝上,从中随机抽取1张,则抽取的卡片上的数是正数的概率为______.
13. 已知m2−8m+1=0,则2m2−8m+1m2= .
14. 如图,把三角形纸片ABC沿ED折叠,使点A落在四边形BCDE外部,已知∠1=80°,∠2=30°,则∠A的度数为______ .
15. 如图,在△ABC中,D,E分别是BC,AD的中点,点F在BE上,且EF=2BF,若S△BCF=2cm2,则S△ABC等于 .
三、解答题(本大题共10小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
16. (本小题8.0分)
计算:
(1)(−2)2+(3.14−π)0−|−2|+(12)−1;
(2)(4x2−2x3+6x)÷(−2x)−(2x−1)2.
17. (本小题8.0分)
如图,已知AB//DC,∠B=30°,∠BEC=62°,下面求∠C的度数,请填写推理的根据:
解:如图,过点E作EF//AB,
∵AB//DC(已知)
∴EF//DC(______ )
∴∠B=∠BEF(______ )
∠C=∠CEF(______ )
∴∠B+∠C=∠BEF+∠CEF(______ )
即∠B+∠C=∠BEC
∴∠C=∠BEC−∠B=62°−30°=32°.
18. (本小题8.0分)
化简求值:
(1)化简求值:5x2−[x2−2x−2(x2−3x+1)],其中3x2−2x−1=0;
(2)已知A=2a2+3ma−2a−1,B=a2+ma−1,且2A−4B的值不含a的一次项,求m的值.
19. (本小题8.0分)
如图:在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形△A′B′C′(不写作法).
(2)若网格上的最小正方形的边长为1,求△ABC的面积.
20. (本小题8.0分)
2022年3月23日,“天宫课堂”第二课在中国空间站正式开讲,航天员王亚平、叶光富、翟志刚为学生们上了一堂豪华的太空课,引发了学生了解科学知识的新热潮.八(1)班社团通过查阅资料发现,声音在空气中传播的速度和气温的变化存在如下的关系:
(1)在这个变化过程中,______ 是自变量,______ 是因变量.
(2)从表中数据可知,气温每升高1℃,声音在空气中传播的速度就提高______ m/s.
(3)声音在空气中的传播速度v/(m/s)与气温t(℃)的关系式可以表示为______ ;
(4)某日的气温为22℃,小乐看到烟花燃放5s后才听到声响,那么小乐与燃放烟花所在地大约相距多远?
21. (本小题9.0分)
2022年“新课标”提出,义务教育劳动课程以丰富开放的劳动项目为载体.南开中学积极发挥劳动教育的融合性特征,从课程设计、课余生活等多维度,鼓励学生积极参与劳动.为了解七年级学生一周参与劳动时间的情况,随机抽取部分学生,统计了他们每周劳动时间(单位:h),并将收集到的数据整理分析,共分为五组:(A:x<1,B:1≤x<2,C:2≤x<3,D:3≤x<4,E:x≥4,其中每周劳动时间不少于3小时为达标),绘制了如下两幅不完整的统计图:
结合图中提供的信息,解答下列问题:
(1)本次调查的总人数为______ 人,a= ______ ;
(2)把频数分布直方图补充完整;
(3)为了让全校学生重视劳动学习,学校准备从这些达标学生中随机抽取1名学生给全校学生分享劳动收获心得,若已知在这些达标学生中有男生13人,求抽中女生的概率.
22. (本小题9.0分)
如图,在△ABC和△BCD中,AC=CD,∠BAC+∠BDC=180°,在BD的延长线上取
点E,使DE=AB,连接CE.
(1)试说明:∠ABC=∠DBC;
(2)连接AD交BC于点F,若∠ABD=60°,∠ADB=40°,试说明:BD=AB+AF.
23. (本小题10.0分)
图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
(1)观察图2,请直接写出代数式(m+n)2,(m−n)2,mn之间的等量关系;
(2)根据(1)中的等量关系,若x+2y=6,xy=4,则x−2y的值为______ ;
(3)已知(2024−a)(2022−a)=1,求(2024−a)2+(2022−a)2的值.
24. (本小题10.0分)
已知△ABC.
(1)如图1,按如下要求用尺规作图:
①作出△ABC的中线CD;
②延长CD至E,使DE=CD,连接AE;(不要求写出作法,但要保留作图痕迹.)
(2)如图2,若∠ACB=90°,CD是中线,试探究CD与AB之间的数量关系,并说明理由;
(3)如图3,若∠ACB=45°,AC=BC,CD是△ABC的中线,过点B作BE⊥AC于E,交CD于点F,连接DE,若CF=4,求DE的长.
25. (本小题12.0分)
如图,在△ABC中,∠ACB=90°,AC=BC,边CA沿着过点A的某条直线对折得到得到DA,连接CD,以CD为边在左侧作△CDE,其中∠CDE=90°,CD=DE,AD与CE交于点F,连接BD.
(1)如图1,连接AE,当点D在△ABC外部时,试说明△ADE≌△BCD;
(2)如图2,连接AE,当点D在△ABC的斜边AB上时,试判断△AEF的形状并说明理由;
(3)如图3,当点D在△ABC的内部时,若点F为AD的中点,且EF=2,求BD的长.
答案和解析
1.【答案】D
【解析】解:选项A、B、C的图形都是轴对称图形,选项D的图形不是轴对称图形.
故选:D.
根据轴对称的定义,即图形沿某条直线折叠后,能与原图形的另一部分重合,据此即可一一判定.
本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】D
【解析】解:A、a2÷a2=1,故A不符合题意;
B、(−a2)3=−a6,故B不符合题意;
C、a2⋅a3=a5,故C不符合题意;
D、(3a)2=9a2,故D符合题意;
故选:D.
利用同底数幂的除法的法则,同底数幂的乘法的法则,幂的乘方与积的乘方的法则对各项进行运算即可.
本题主要考查同底数幂的除法,幂的乘方与积的乘方,同底数幂的乘法,解答的关键是对相应的运算法则的掌握.
3.【答案】D
【解析】解:A、一名射击运动员射击一次,中靶,是随机事件,故A不符合题意;
B、彩票的中奖率是15%,那么买100张彩票不一定有15张中奖,故B不符合题意;
C、掷一枚质地均匀的骰子,掷出的点数是质数,是随机事件,故C不符合题意;
D、一个三角形,其任意两边之和大于第三边,是必然事件,故D符合题意;
故选:D.
根据概率的意义,随机事件,必然事件,不可能事件的定义,逐一判断即可解答.
本题考查了概率的意义,随机事件,熟练掌握随机事件,必然事件,不可能事件的特点是解题的关键.
4.【答案】D
【解析】解:A、当h=70cm时,t=1.59s,原说法错误,该选项不符合题意;
B、随着h逐渐升高,t逐渐变小,原说法错误,该选项不符合题意;
C、h每增加10cm,t减小的值不一定,原说法错误,该选项不符合题意;
D、随着h逐渐升高,小车下滑的平均速度逐渐加快,该选项符合题意.
故选:D.
根据表格中的数据,分析其中的规律,即可做出正确的判断.
根据表格中的数据,分析其中的规律,即可做出正确的判断.
5.【答案】C
【解析】解:∵∠2=∠5,
∴m//n,
故A不符合题意;
∵∠3+∠4=180°,
∴m//n,
故B不符合题意;
由∠3=∠5,不能判定m//n,
故C符合题意;
∵∠1=∠6,
∴m//n,
故D不符合题意;
故选:C.
根据平行线的判定定理求解即可.
此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
6.【答案】D
【解析】解:A、添加∠B=∠D,由“AAS”可证△ABC≌△ADE,故选项A不合题意;
B、添加BC=DE,由“SAS”可证△ABC≌△ADE,故选项B不合题意;
C、添加∠1=∠2,由“ASA”可证△ABC≌△ADE,故选项C不合题意;
D、添加AB=AD,不能证明△ABC≌△ADE,故选项D符合题意;
故选:D.
由全等三角形的判定依次判断可求解.
本题考查了全等三角形的判定,熟练掌握全等三角形的判定是本题的关键.
7.【答案】D
【解析】解:根据折叠的性质可得,∠EFC=∠EFC′=118°,∠GEF=∠DEF,
∴∠EFG=180°−∠EFC=180°−118°=62°,
∵四边形ABCD是长方形,
∴AD//BC,
∴∠DEF=∠EFG=62°,
∴∠GEF=∠DEF=62°,
∴∠1=∠GEF+∠EFG=62°+62°=124°,
故选:D.
首先根据折叠的性质可得,∠EFC=∠EFC′=118°,可求得∠EFG=62°,再根据平行线及折叠的性质,可求得∠GEF=∠DEF=∠EFG=62°,再由三角形的外角性质,即可求解.
本题考查了折叠的性质,平行线的性质以及三角形的外角性质,熟练掌握和运用折叠的性质是解决本题的关键.
8.【答案】D
【解析】解:由已知得:PC=BC−BP=(10−4t)cm;
①若△ABP≌△PCQ.
则AB=PC=6cm,
∴6=10−4t,
∴t=1.
∴a=4;
②若△ABP≌△QCP.
则AB=CQ=6cm,BP=CP=(10−4t)cm,则t=54.
得:54a=6.
解得:a=245.
综上,a的值为4或245.
故选:D.
先表示出CP长度,分△BPA≌△CPQ和△BPA≌△CQP两种情况进行解答.
本题考查的是矩形的性质和全等三角形的性质,正确运用数形结合思想和分类讨论思想是解题的关键.
9.【答案】B
【解析】解:根据题意得:图1中阴影部分的面积为(a−b)2,
图2中阴影部分的面积a2−2ab+b2,
根据图1与图2中阴影部分的面积相等可得(a−b)2=a2−2ab+b2.
故选:B.
根据图形确定出图1与图2中阴影部分的面积,即可作出判断.
此题考查了完全平方公式的几何背景,弄清阴影部分面积的求法是解本题的关键.
10.【答案】A
【解析】解:∵△ABC为等边三角形,
∴AB=BC=CA,∠B=∠BCA=∠CAB=60°.
①∵点F为AC的中点,
∴CF=FA=12AC,
又CE=12BC,BC=AC,
∴CE=CF,
∴∠E=∠CFE,
∵∠BCA=∠E+∠CFE=60°,
∴∠E=∠CFE=30°,
∴∠AFG=∠CFE=30°,
∴∠AGE=180°−∠CAB−∠AFG=180°−60°−30°=90°,
∴EG⊥AB,
∴结论①正确;
②设AG=a,
由①正确可知:∠AGE=90°,∠AFG=30°,
∴FA=2a,FG= 3a,
∴AC=BC=AB=4a,
∴BG=AB−AG=3a,BE=BC+CE=4a+2a=6a,
在Rt△BEG中,BG=3a,BE=6a,
由勾股定理得:EG= BE2−BG2=3 3a,
∴EF=GE−FG=3 3a− 3a=2 3a,
∴EF=2FE,
∴结论②正确;
③过点N作NH⊥AC于点H,连接BN,如图所示:
∵MN为BG的垂直平分线,
∴BN=GN,∠GMN=90°,
∵△ABC为等边三角形,AD⊥BC,
∴∠BAD=∠CAD=30°,AD为BC的垂直平分线,
∴MN=HN,BN=CN,
∴GN=CN,
在Rt△GMN和Rt△CHN中,
GN=CNMN=HN,
∴Rt△GMN≌Rt△CHN(HL),
∴∠GNM=∠CNH,
∵∠BAD=∠CAD=30°,∠GMN=90°,NH⊥AC,
∴∠ANM=∠ANH=60°,
∴∠GNC=∠ANG+∠ANH+∠GNM=∠ANM+∠ANH=120°,
∴结论③正确;
④设AG=a,MN=b,
由②可知:BG=3a,AC=4a,
由③可知:NH=MN=b,MG=12BG=3a2,
∴S△MGN=12MG⋅MN=12⋅3a2⋅b=3ab4,
又S△ANG=12AG⋅MN=12⋅a⋅b=ab2,S△ANC=12AC⋅NH=12⋅4ab=2ab,
∴S四边形AGNC=S△ANG+S△ANC=ab2+2ab=5ab2,
∴S四边形AGNC≠4S△MGN,
∴结论④不正确.
综上所述:正确的结论是①②③.
故选:A.
①由点F为AC的中点,CE=12BC可得CE=CF,据此可求出∠E=∠CFE=30°,进而可求得∠AGE=90°,据此可对结论①进行判断;
②设AG=a,则FA=2a,FG= 3a,AC=BC=AB=4a,BG=3a,BE=6a,进而在Rt△BEG中由勾股定理得EG=3 3a,据此可对结论②进行判断;
③过点N作NH⊥AC于点H,连接BN,先证GN=CN,MN=HN,进而依据“HL”判定Rt△GMN和Rt△CHN全等得∠GNM=∠CNH,最后再根据∠ANM=∠ANH=60°可得∠GNC的度数,进而可对结论③进行判断;
④设AG=a,MN=b,由②可知BG=3a,AC=4a,由③可:NH=MN=b,MG=12BG=3a2,于是可求出S△MGN=3ab4,S△ANG=ab2,S△ANC=2ab,则S四边形AGNC=5ab2,据此可对结论④进行判断,综上所述即可得出答案.
此题主要考查了等边三角形的性质,直角三角形的性质,全等三角形的判定和性质,三角形的面积,线段垂直平分线的性质等,解答此题的关键是熟练掌握全等三角形的判定方法,理解等边三角形相关性质,在直角三角形中,30°的角所对的边等于斜边的一半,线段垂直平分线上的点到线段两端的距离相等.
11.【答案】50°
【解析】解:∵OE⊥CD,
∴∠EOD=90°,
∵∠BOE=40°,
∴∠BOD=90°−40°=50°,
∴∠AOC=∠BOD=50°.
故答案为:50°.
直接利用垂直的定义结合对顶角的性质得出答案.
此题主要考查了垂线以及对顶角,正确得出∠BOD的度数是解题关键.
12.【答案】35
【解析】解:∵|−3|=3,(−2)2=4,−(−14)0=−1,(−1)−2=1,
∴5个数在有3个正数,
∴从中随机抽取1张,则抽取的卡片上的数是正数的概率为35.
故答案为:35.
先化简给出的各数,然后找出正数的个数,再根据概率公式可得答案.
此题主要考查了概率公式和应用,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
13.【答案】61
【解析】解:∵m2−8m+1=0,m≠0,
∴m+1m=8,m2−8m=−1,
两边平方得:(m+1m)2=64,
∴m2+1m2+2=64,即m2+1m2=62,
则原式=(m2−8m)+(m2+1m2)
=−1+62
=61.
故答案为:61.
根据m不为0,已知等式两边除以m表示求出m+1m的值,平方并利用完全平方公式化简求出m2+1m2的值,原式变形后代入计算即可求出值.
此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
14.【答案】25°
【解析】解:如图,设AC与A′E交于点M,
由折叠性质可得∠A′=∠A,
∵∠1=∠A+∠AME,∠AME=∠2+∠A′,
∴∠1=∠A+∠2+∠A′=2∠A+∠2,
∵∠1=80°,∠2=30°,
∴2∠A+30°=80°,
∴∠A=25°,
故答案为:25°.
设AC与A′E交于点M,然后利用折叠性质及三角形的外角性质可得∠1=2∠A+∠2,结合已知条件计算即可.
本题考查折叠性质及三角形的外角性质,结合已知条件求得∠1=2∠A+∠2是解题的关键.
15.【答案】12cm2
【解析】解:如图,∵EF=2BF,S△BCF=2cm2,
∴S△BEC=3S△BCF=3×2=6cm2,
∵D是BC的中点,
∴S△BDE=S△CDE=12S△BEC=3cm2,
∵E是AD的中点,
∴S△ABD=S△ACD=2S△BDE=6cm2,
∴S△ABC=2S△ABD=12cm2,
∴△ABC的面积为12cm2,
故答案为:12cm2.
根据EF=2BF,S△BCF=2cm2,求得S△BEC=3S△BCF=6cm2,根据三角形中线把三角形分成两个面积相等的三角形可得S△BDE=S△CDE=12S△BEC=3cm2,从而求出S△ABD=S△ACD=2S△BDE=6cm2,再根据S△ABC=2S△ABD计算即可得解.
本题考查了三角形的面积,解题主要利用了三角形中线把三角形分成两个面积相等的三角形,理论依据是等底等高的三角形的面积相等,需熟记.
16.【答案】解:(1)原式=4+1−2+2
=5;
(2)原式=−2x+x2−3−4x2+4x−1
=−3x2+2x−4.
【解析】(1)根据幂的乘方,零指数幂,负指数幂的性质求解即可;
(2)先计算乘除,后计算加减可得结论.
本题考查整式的加减,实数的运算等知识,解题的关键是掌握整式的混合运算的法则,属于中考常考题型.
17.【答案】两条直线都与第三条直线平行,那么这两条直线平行 两直线平行,内错角相等 两直线平行,内错角相等 等量代换
【解析】解:∵AB//DC,EF//AB,
∴EF//DC(两条直线都与第三条直线平行,那么这两条直线平行),
∴∠B=∠BEF(两直线平行,内错角相等),
∠C=∠CEF(两直线平行,内错角相等),
∴∠B+∠C=∠BEF+∠CEF,(等量代换),
即∠B+∠C=∠BEC,
∴∠C=∠BEC−∠B=62°−30°=32°.
故答案为:两条直线都与第三条直线平行,那么这两条直线平行;两直线平行,内错角相等;两直线平行,内错角相等;等量代换.
根据平行线的性质解答即可.
本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a//b,b//c⇒a//c.
18.【答案】解:(1)原式=5x2−x2+2x+2(x2−3x+1)
=5x2−x2+2x+2x2−6x+2
=6x2−4x+2,
∵3x2−2x−1=0,
∴3x2−2x=1,
∴6x2−4x=2,
∴原式=2+2=4;
(2)∵A=2a2+3ma−2a−1,B=a2+ma−1,
∴2A−4B
=2(2a2+3ma−2a−1)−4(a2+ma−1)
=4a2+6ma−4a−2−4a2−4ma+4
=2ma−4a+2,
∵2A−4B的值不含a的一次项,
∴2m−4=0,
解得:m=2.
【解析】(1)先去括号,再合并同类项,最后整体代换即可求出答案;
(2)先化简2A−4B,根据不含a的一次项,即可求出m的值.
本题主要考查了整式的加减—化简求值,掌握去括号法则和合并同类项法则是解题的关键.
19.【答案】解:(1)如图所示:△A′B′C′即为所求;
(2)△ABC的面积为:2×3−12×1×2−12×1×3−12×1×2=2.5
【解析】此题主要考查了轴对称变换以及三角形面积求法,正确得出对应点位置是解题关键.
(1)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(2)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案.
20.【答案】气温 声音在空气中的传播速度 0.6 v=331+0.6t
【解析】解:(1)根据题意可知,气温是自变量,声音在空气中的传播速度是因变量,
故答案为:气温,声音在空气中的传播速度;
(2)由表中数据可知,气温每升高1℃,声音在空气中传播的速度就提高3÷5=0.6m/s,
故答案为:0.6;
(3)由表格中两个变量对应值的变化规律可得,v=331+3t5=331+0.6t,
故答案为:v=331+0.6t;
(4)当t=22时,v=331+13.2=344.2(m/s),
344.2×5=1721(m),
答:小乐与燃放烟花所在地大约相距1721m.
(1)根据题意和表格中的两个量的变化关系得出答案;
(2)从表格中两个变量对应值的变化规律得出答案;
(3)利用(2)中的变化关系得出函数关系式;
(4)当t=22时,求出v,再根据路程等于速度乘以时间进行计算即可.
本题考查函数的表示方法,常量与变量,理解常量与变量的定义,求出函数的关系式是正确解答的前提.
21.【答案】50 36
【解析】解:(1)12÷24%=50(人),
即调查的总人数为60人,
a%=1850=36%,a=36.
故答案为50,36;
(2)B组人数为50−(2+12+18+10)=8(人).
补全频数分布直方图如图所示:
(3)∵每周劳动时间不少于3小时为达标,
∴达标总人数为18+10=28(人),
∵这些达标学生中有男生13人,
∴女生有28−13=15(人),
∴抽中女生的概率为1528.
(1)根据C组的频数和百分比求出总人数,再用D组频数除以总人数求出a的值;
(2)先求出B组人数,再补全频数分布直方图;
(3)用达标学生中女生的人数除以达标总人数即可.
本题考查频数分布直方图、扇形统计图、概率公式等知识,解题的关键是掌握基本概念,属于中考常考题型.
22.【答案】解:(1)∵∠BAC+∠BDC=180°,∠CDE+∠BDC=180°,
∴∠CDE=∠BAC,
在△BAC和△EDC中,
AC=CD∠BAC=∠CDEAB=DE,
∴△BAC≌△EDC(SAS),
∴∠ABC=∠CEB,BC=CE,
∴∠CEB=∠CBE,
∴∠ABC=∠DBC;
(2)如图,在BD上截取BH=AB,连接FH,
∵∠ABD=60°,∠ADB=40°,
∴∠BAD=80°,
在△ABF和△HBF中,
AB=BH∠ABF=∠HBFBF=BF,
∴△ABF≌△HBF(SAS),
∴∠BAD=∠BHF=80°,AF=FH,
∵∠BHF=∠ADB+∠DFH,
∴∠DFH=40°=∠ADB,
∴DH=FH=AF,
∴BD=BH+DH=AB+AF.
【解析】(1)由“SAS”可证△BAC≌△EDC,可得∠ABC=∠CEB,BC=CE,由等腰三角形的性质可得∠ABC=∠CEB=∠CBE;
(2)由“SAS”可证△ABF≌△HBF,可得∠BAD=∠BHF=80°,AF=FH,可证FH=DH,即可得结论.
本题考查了全等三角形的判定和性质,等腰三角形的性质,角平分线的性质,添加恰当辅助线构造全等三角形是解题的关键.
23.【答案】±2
【解析】解:(1)图2中阴影部分是边长为(m−n)的正方形,因此阴影部分面积为(m−n)2;
图2中阴影部分面积也可以看作从边长为(m+n)的正方形面积减去4个长为m,宽为n的长方形面积,即(m+n)2−4mn,
因此有(m−n)2=(m+n)2−4mn;
(2)由(1)可知,
(x−2y)2=(x+2y)2−4x⋅2y
=(x+2y)2−8xy
=62−8×4
=36−32
=4,
∴x−2y=± 4=±2,
故答案为:±2;
(3)设x=2024−a,y=2022−a,则x−y=2,xy=(2024−a)(2022−a)=1,
∴(2024−a)2+(2022−a)2
=x2+y2
=(x−y)2+2xy
=4+2
=6,
答:(2024−a)2+(2022−a)2的值为6.
(1)由拼图可知图2中阴影部分是边长为(m−n)的正方形,可表示面积;大正方形面积减去四个长方形面积也可以得出阴影部分的面积,进而得出关系式;
(2)由(1)得(x−2y)2=(x+2y)2−4x⋅2y,再代入计算即可;
(3)设x=2024−a,y=2022−a,由题意可得x−y=2,xy=1,根据
x2+y2=(x−y)2+2xy,求出x2+y2的值即可.
本题考查了完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的关键.
24.【答案】解:(1)①如图1所示,线段CD即为所求.
②如图1中,线段DE,AE即为所求.
(2)AB与CD的数量关系是:AB=2CD,理由如下:
如图2,延长CD至E,使DE=DC,连接BE,
∵CD是中线,
∴AD=BD,
在△ADC和△BDE中,
AD=BD∠ADC=∠BDEDC=DE,
∴△ADC≌△BDE(SAS),
∴∠E=∠ACD,AC=BE,
∴AC//BE,
∴∠ACB+∠EBC=180°,
∵∠ACB=90°,
∴∠EBC=90°,
在△ACB和△EBC中,
AC=BE∠ACB=∠EBCCB=BC,
∴△ACB≌△EBC(SAS),
∴AB=CE,
∵CE=2CD,
∴AB=2CD.
(3)∵BE⊥AC,∠ACB=45°,
∴∠CEB=∠BEA=90°,∠ECB=∠EBC=45°,
∴EC=EB,
∵AC=BC,CD是中线,
∴CD⊥AB,
∵∠CEF=∠BDF=90°,∠CFE=∠BFD,
∴∠ECF=∠ABE,
在△CEF和△BEA中,
∠ECF=∠EBACE=BE∠CEF=∠BEA,
∴△CEF≌△BEA(ASA),
∴CF=AB=4,
∵AD=BD,∠AEB=90°,
∴DE=12AB=2.
【解析】(1)①根据三角形的中线的定义作出图形即可;
②根据要求作出图形即可;
(2)结论:AB=2CD.利用全等三角形的判定和性质证明即可;
(3)利用全等三角形的性质证明AB=CF,再利用(2)中结论解决问题.
本题是三角形综合题,考查了三角形的中线的定义,直角三角形斜边中线的性质,全等三角形的判定和性质等知识,解题的关键是学会倍长中线,构造全等三角形解决问题,属于中考常考题型.
25.【答案】(1)证明:如图1中,
∵AC=AD,
∴∠ACD=∠ADC,
∵∠ACB=∠CDE=90°,
∴∠BCD+∠ACD=90°,∠ADC+∠ADE=90°,
∴∠BCD=∠ADE,
∵CA=CB,AC=AD,
∴DA=CB,
在Rt△ADE和△BCD中,
DA=CB∠ADE=∠BCDDE=CD,
∴△ADE≌△BCD(SAS);
(2)解:结论:△AEF是等腰三角形.
理由:如图2中,
∵CA=CB,∠ACB=90°,
∴∠CAB=∠B=45°,
∵AC=AD,
∴∠ACD=∠ADC=75°,
∵△ADE≌△BCD,
∴∠DAE=∠B=45°,
∴∠EAF=∠DCF,
∵∠AFE=∠CFD,
∴∠AEF=∠CDF=67.5°,
∴∠AFE=180°−45°−67.5°=67.5°,
∴∠AFE=∠AEF=67.5°,
∴△AEF是等腰三角形;
(3)解:如图3中,延长CF到T,使得FT=CF,连接AT,DT.
∵AF=DF,CF=FT,
∴四边形ATDC是平行四边形,
∴AC=DT,AC//DT,
∴∠CAD=∠ADT,
∵AC=AD,
∴DA=DT,
∵∠ACD+∠DCB=90°,∠CAD+2∠ACD=180°,
∴12∠CAD+∠ACD=90°,
∴∠DCB=12∠CAD,
∴∠CAD=∠ADT=2∠DCB,
∵∠DCB=∠ADE,
∴∠ADE=∠TDE,
∵DA=DT,
∴DE⊥AT,
∴DE平分AT,
∵AF=FD,
∴点E是△ADT是重心,
∴ET=2EF=4,
∵DE垂直平分线段AT,
∴EA=ET=4,
∵△ADE≌△BCD,
∴BD=AE=4.
【解析】(1)根据SAS证明三角形全等即可;
(2)△AEF是等腰三角形.证明∠AEF=∠AFE=75°即可;
(3)如图3中,延长CF到T,使得FT=CF,连接AT,DT.证明△ADT是等腰三角形,推出点E是三角形的重心,可得ET=2EF=4,再证明EA=ET,可得结论.
本题属于几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,等腰三角形的判定和性质,三角形的重心的性质,属于中考压轴题.
支撑物的高度h(cm)
10
20
30
40
50
60
70
小车下滑的时间t(s)
4.23
3.00
2.45
2.13
1.89
1.71
1.59
气温t/℃
0
5
10
15
20
25
声音在空气中的传播速度v/(m/s)
331
334
337
340
343
346
2022-2023学年四川省达州市达川区南岳初级中学八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年四川省达州市达川区南岳初级中学八年级(下)期末数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年四川省达州市达川区石梯中学八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年四川省达州市达川区石梯中学八年级(下)期末数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年四川省达州市达川区石梯中学八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年四川省达州市达川区石梯中学八年级(下)期末数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












