


2022-2023学年湖南省长沙市湖南师大附中博才实验中学七下数学期末质量跟踪监视试题含答案
展开2022-2023学年湖南省长沙市湖南师大附中博才实验中学七下数学期末质量跟踪监视试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.如图,![]() 是一钢架,且
是一钢架,且![]() ,为使钢架更加牢固,需在其内部添加-一些钢管
,为使钢架更加牢固,需在其内部添加-一些钢管![]() 、
、![]() 、
、![]() ,添加的钢管都与
,添加的钢管都与![]() 相等,则最多能添加这样的钢管( )
相等,则最多能添加这样的钢管( )
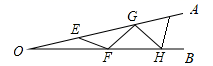
A.![]() 根 B.
根 B.![]() 根 C.
根 C.![]() 根 D.无数根
根 D.无数根
2.在四边形![]() 中,若
中,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.不等式组![]() 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.当x=3时,函数y=-2x+1的值是( )
A.3 B.-5 C.7 D.5
5.如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
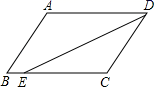
A.2cm B.4cm C.6cm D.8cm
6.如图,直线![]() 与
与![]() 分别交x轴于点
分别交x轴于点![]() ,
,![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
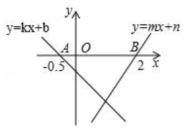
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
7.某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分,90分,88分,则小彤这学期的体育成绩为()
A.89分 B.90分 C.92分 D.93分
8.在平面直角坐标系中,下列各点位于第四象限的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为![]() ,再分别取A1C、B1C的中点A2、B2,取A2C、B2C的中点A3、B3,依次取下去…利用这一图形,能直观地计算出
,再分别取A1C、B1C的中点A2、B2,取A2C、B2C的中点A3、B3,依次取下去…利用这一图形,能直观地计算出![]() ( )
( )
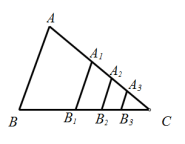
A.1 B.![]() C.
C.![]() D.
D.![]()
10.方程x2+x﹣12=0的两个根为( )
A.x1=﹣2,x2=6 B.x1=﹣6,x2=2 C.x1=﹣3,x2=4 D.x1=﹣4,x2=3
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若实数a、b满足a2—7a+2=0和b2—7b+2=0,则式子![]() 的值是____.
的值是____.
12.平面直角坐标系中,点M(-3,-4)到x轴的距离为______________________.
13.已知:x=![]() ,y=
,y=![]() .那么
.那么![]() ______.
______.
14.如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
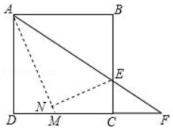
15.某高科技开发公司从2013年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是____________.
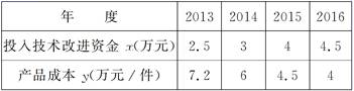
16.如图,已知边长为4的菱形ABCD中,AC=BC,E,F分别为AB,AD边上的动点,满足BE=AF,连接EF交AC于点G,CE、CF分别交BD与点M,N,给出下列结论:①∠AFC=∠AGE;②EF=BE+DF;③△ECF面积的最小值为3![]() ,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)解不等式组: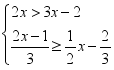 ,并把解集表示在数轴上.
,并把解集表示在数轴上.
18.(8分)如图,![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)如图①,若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)如图②,![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,满足
,满足![]() ,
,![]() .求证:
.求证:![]() .
.
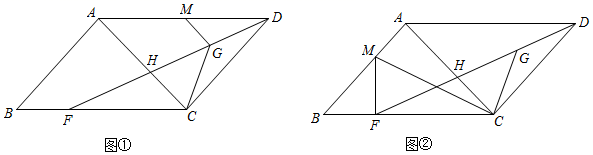
19.(8分)如图,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2,直线MN:y=x﹣4沿x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图2所示.
(1)点A的坐标为 ,矩形ABCD的面积为 ;
(2)求a,b的值;
(3)在平移过程中,求直线MN扫过矩形ABCD的面积S与t的函数关系式,并写出自变量t的取值范围.
20.(8分)当![]() 在什么范围内取值时,关于
在什么范围内取值时,关于![]() 的一元一次方程
的一元一次方程![]() 的解满足
的解满足![]() ?
?
21.(8分)求下列分式的值:![]() ,并从x=0,﹣1,﹣2中选一个适当的值,计算分式的值.
,并从x=0,﹣1,﹣2中选一个适当的值,计算分式的值.
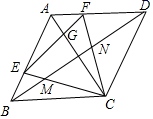
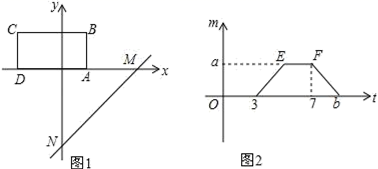
22.(10分)如图,点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点.
(1)如果图中线段都可画成有向线段,那么在这些有向线段所表示的向量中,与向量![]() 相等的向量是 ;
相等的向量是 ;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .试用向量
.试用向量![]() ,
,![]() 或
或![]() 表示下列向量:
表示下列向量:![]() = ;
= ;![]() = .
= .
(3)求作:![]()
![]() .(请在原图上作图,不要求写作法,但要写出结论)
.(请在原图上作图,不要求写作法,但要写出结论)
23.(10分)如图,四边形![]() 为菱形,已知
为菱形,已知![]() ,
,![]() .
.
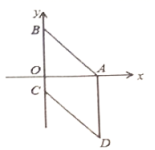
(1)求点![]() 的坐标;
的坐标;
(2)求经过点![]() ,
,![]() 两点的一次函数的解析式.
两点的一次函数的解析式.
(3)求菱形![]() 的面积.
的面积.
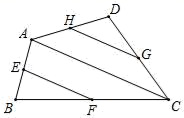
24.(12分)阅读下列材料:
数学课上,老师出示了这样一个问题:
如图1,正方形为![]() 中,点
中,点![]() 、
、![]() 在对角线
在对角线![]() 上,且
上,且![]() ,探究线段
,探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察和度量,发现图1中线段![]() 与
与![]() 相等”;
相等”;
小伟:“通过构造![]() (如图2),证明三角形全等,进而可以得到线段
(如图2),证明三角形全等,进而可以得到线段![]() 、
、![]() 、
、![]() 之间的数量关系”.
之间的数量关系”.
老师:“此题可以修改为‘正方形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上,延长
上,延长![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() (如图3).如果给出
(如图3).如果给出![]() 、
、![]() 的数量关系与
的数量关系与![]() 、
、![]() 的数量关系,那么可以求出
的数量关系,那么可以求出![]() 的值”.
的值”.
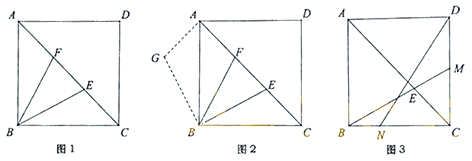
请回答:
(1)求证:![]() ;
;
(2)探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(3)若![]() ,
,![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、B
4、B
5、A
6、D
7、B
8、D
9、C
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() .
.
12、1
13、98
14、![]()
15、y=![]()
16、①③④
三、解下列各题(本大题共8小题,共72分)
17、-2≤x<2
18、(1)![]() (2)见解析
(2)见解析
19、(4)(4,7),3 ;(3)a=a=3![]() ,b=6;(3)S=
,b=6;(3)S=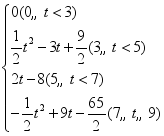 .
.
20、![]()
21、-1
22、(1)![]() ;(2)
;(2)![]() +
+![]() 、
、![]() +
+![]() ﹣
﹣![]() ;(3)如图所示见解析.
;(3)如图所示见解析. ![]() .
.
23、(1)C(0,![]() );(2)
);(2)![]() ;(3)1
;(3)1
24、(1)详见解析;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]()
湖南省长沙市明德中学2022-2023学年七下数学期末质量跟踪监视模拟试题含答案: 这是一份湖南省长沙市明德中学2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列函数中,是反比例函数的为等内容,欢迎下载使用。
湖南省长沙市大附中博才实验中学2022-2023学年七下数学期末达标检测试题含答案: 这是一份湖南省长沙市大附中博才实验中学2022-2023学年七下数学期末达标检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列说法错误的是等内容,欢迎下载使用。
湖南省师大附中博才实验中学2022-2023学年七下数学期末统考试题含答案: 这是一份湖南省师大附中博才实验中学2022-2023学年七下数学期末统考试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列事件属于必然事件的是,已知点在轴上,则点的坐标是等内容,欢迎下载使用。












