


2022-2023学年湖南省江华瑶族自治县七下数学期末经典试题含答案
展开2022-2023学年湖南省江华瑶族自治县七下数学期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列语句描述的事件中,是不可能事件的是( )
A.只手遮天,偷天换日 B.心想事成,万事如意
C.瓜熟蒂落,水到渠成 D.水能载舟,亦能覆舟
2.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设( )
A.三角形中有一个内角小于或等于60° B.三角形中有两个内角小于或等于60°
C.三角形中有三个内角小于或等于60° D.三角形中没有一个内角小于或等于60°
3.如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于( )
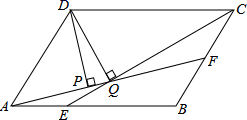
A.3∶4 B.![]() ∶
∶![]() C.
C.![]() ∶
∶![]() D.
D.![]() ∶
∶![]()
4.对于函数 y=3-x,下列结论正确的是( )
A.y 的值随 x 的增大而增大 B.它的图象必经过点(-1,3)
C.它的图象不经过第三象限 D.当 x>1 时,y<0.
5.下列等式一定成立的是( )
A.![]() -
-![]() =
=![]() B.∣2-
B.∣2-![]() =2-
=2-![]() C.
C.![]() D.-
D.-![]() =-4
=-4
6.若最简二次根式2![]() 与
与![]() 是同类二次根式,则a的值为( )
是同类二次根式,则a的值为( )
A.![]() B.2 C.﹣3 D.
B.2 C.﹣3 D.![]()
7.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
选 手 | 甲 | 乙 | 丙 | 丁 |
平均数(环) | 9.2 | 9.2 | 9.2 | 9.2 |
方差(环2) | 0.035 | 0.015 | 0.025 | 0.027 |
则这四人中成绩发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
8.甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的是( )
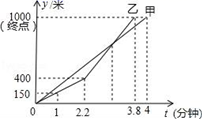
A.甲队率先到达终点 B.甲队比乙队多走了200米路程
C.乙队比甲队少用0.2分钟 D.比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快
9.将函数![]() 的图象向下平移3个单位,则得到的图象相应的函数表达式为
的图象向下平移3个单位,则得到的图象相应的函数表达式为![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.下列说法正确的是( )
A.对应边都成比例的多边形相似 B.对应角都相等的多边形相似
C.边数相同的正多边形相似 D.矩形都相似
11.如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
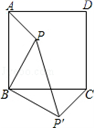
A.2![]() B.3
B.3![]() C.3 D.无法确定
C.3 D.无法确定
12.直线l1:y=ax+b与直线l2:y=mx+n在同一平面直角坐标系中的图象如图所示,则关于x的不等式ax+b<mx+n的解集为( )
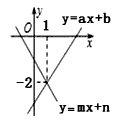
A.x>﹣2 B.x<1 C.x>1 D.x<﹣2
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.不等式2x≥-4的解集是 .
14.一次函数y=(m+2)x+3-m,若y随x的增大而增大,函数图象与y轴的交点在x轴的上方,则m的取值范围是____.
15.已知5个数![]() 的平均数为
的平均数为![]() ,则
,则![]() 这六个数的平均数为___
这六个数的平均数为___
16.点M(a,﹣5)与点N(﹣2,b)关于x轴对称,则a+b=________.
17.如图,在菱形ABCD中,AB=5,对角线AC=1.若过点A作AE⊥BC,垂足为E,则AE的长为_________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)阅读下面的解题过程,解答后面的问题:
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 点的坐标;
点的坐标;
解:分别过![]() ,
,![]() 做
做![]() 轴的平行线,过
轴的平行线,过![]() ,
,![]() 做
做![]() 轴的平行线,两组平行线的交点如图
轴的平行线,两组平行线的交点如图![]() 所示,设
所示,设![]() ,则
,则![]() ,
,![]() ,
,![]()
由图![]() 可知:
可知:
![]()
![]()
![]() 线段
线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]()
(应用新知)
利用你阅读获得的新知解答下面的问题:
(1)已知![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为
(2)平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,利用中点坐标公式求点
,利用中点坐标公式求点![]() 的坐标。
的坐标。
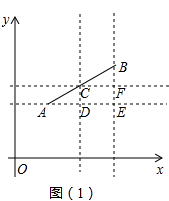
(3)如图![]() ,点
,点![]() 在函数
在函数![]() 的图象上,
的图象上, ![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() 在函数
在函数![]() 的图象上 ,以
的图象上 ,以![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点,且以
四个点为顶点,且以![]() 为一边构成平行四边形,直接写出所有满足条件的
为一边构成平行四边形,直接写出所有满足条件的![]() 点坐标。
点坐标。
19.(5分)如图,在直角坐标系中,每个小方格都是边长为![]() 的正方形,
的正方形,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标是
的坐标是![]() .
.
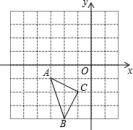
![]() 先将
先将![]() 沿
沿![]() 轴正方向向上平移
轴正方向向上平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向向左平移
轴负方向向左平移![]() 个单位长度得到
个单位长度得到![]() ,画出
,画出![]() ,点
,点![]() 坐标是________;
坐标是________;
![]() 将
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,画出
,画出![]() ,并求出点
,并求出点![]() 的坐标是________;
的坐标是________;
![]() 我们发现点
我们发现点![]() 、
、![]() 关于某点中心对称,对称中心的坐标是________.
关于某点中心对称,对称中心的坐标是________.
20.(8分)(1)计算:5![]() -
-![]() +2
+2![]()
(2)解不等式组: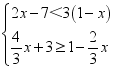
21.(10分)如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、DQ、CQ、BQ,设AP=x.
(1)BQ+DQ的最小值是_______,此时x的值是_______;
(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.
①求证:点E是CD的中点; ②求x的值.
(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.

22.(10分)如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,,
,,![]()
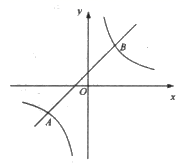
(1)求反比例函数与一次函数的函数表达式
(2)请结合图像直接写出不等式![]() 的解集;
的解集;
(3)若点P为x轴上一点,△ABP的面积为10,求点P的坐标,
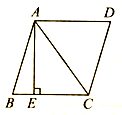
23.(12分)如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=1.
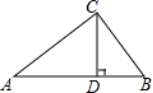
(1)求CD,AD的值;
(2)判断△ABC的形状,并说明理由.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、D
3、B
4、C
5、D
6、B
7、B
8、C
9、B
10、C
11、B
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、x≥-1
14、-2<m<1
15、![]()
16、2
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、 (1)线段![]() 的中点坐标是
的中点坐标是![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)符合条件的
;(3)符合条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.
19、![]() ,
, ![]() ,
, ![]() .
.
20、(1)5![]() ;(2)-1≤x<1.
;(2)-1≤x<1.
21、(1)![]() ,
,![]() ;(3) ①理由详见解析;②
;(3) ①理由详见解析;②![]() ;(3) 3﹣
;(3) 3﹣![]() 或
或![]() 或3+
或3+![]() .
.
22、(1)![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() ;(3)点P的坐标为(3,0)或(-5,0).
;(3)点P的坐标为(3,0)或(-5,0).
23、(1)12,16;(2)△ABC为直角三角形,理由见解析
湖南省长沙青雅丽发中学2022-2023学年七下数学期末经典试题含答案: 这是一份湖南省长沙青雅丽发中学2022-2023学年七下数学期末经典试题含答案,共7页。
湖南省武冈市洞庭学校2022-2023学年七下数学期末经典模拟试题含答案: 这是一份湖南省武冈市洞庭学校2022-2023学年七下数学期末经典模拟试题含答案,共7页。试卷主要包含了下列图案中,中心对称图形的是等内容,欢迎下载使用。
湖南省娄底新化县联考2022-2023学年七下数学期末经典模拟试题含答案: 这是一份湖南省娄底新化县联考2022-2023学年七下数学期末经典模拟试题含答案,共7页。试卷主要包含了甲、乙两车从A城出发前往B城,下列函数中,一次函数的是等内容,欢迎下载使用。












