

2022-2023学年湖北省武汉第二初级中学七年级数学第二学期期末学业质量监测试题含答案
展开2022-2023学年湖北省武汉第二初级中学七年级数学第二学期期末学业质量监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如图,∠BAC=90°,四边形ADEB、BFGC、CHIA均为正方形,若 S四边形ADEB=6,S四边形BFGC=18,四边形CHIA的周长为( )
A.4![]() B.8
B.8![]() C.12
C.12![]() D.8
D.8![]()
2.如图,在▱ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
A.2个 B.3个 C.4个 D.5个
3.如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )
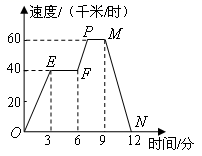
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
4.若关于x的方程![]() 的一个根是3,则m-n的值是
的一个根是3,则m-n的值是
A.-1 B.-3 C.1 D.3
5.下列事件中,必然事件是( )
A.“奉贤人都爱吃鼎丰腐乳”
B.“2018年上海中考,小明数学考试成绩是满分150分”
C.“10只鸟关在3个笼子里,至少有一只笼子关的鸟超过3只”
D.“在一副扑克牌中任意抽10张牌,其中有5张A”
6.小黄在自家种的西瓜地里随意称了10个西瓜,重量(单位:斤)分别是:
5,8,6,8,10,1,1,1,7,1.
按市场价西瓜每斤2元的价格计算,你估算一下,小黄今天卖了350个西瓜约收入( )
A.160元 B.700元 C.5600 D.7000
7.下列各式中,正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若![]() ,则下列不等式中成立的是( )
,则下列不等式中成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
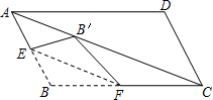
9.如图,将两块完全相同的矩形纸片ABCD和矩形纸片AEFG按图示方式放置(点A、D、E在同一直线上),连接AC、AF、CF,已知AD=3,DC=4,则CF的长是( )
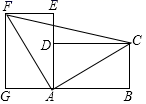
A.5 B.7 C.5![]() D.10
D.10
10.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
二、填空题(本大题共有6小题,每小题3分,共18分)
11.点A(2,1)在反比例函数y=![]() 的图象上,当1<x<4时,y的取值范围是 .
的图象上,当1<x<4时,y的取值范围是 .
12.若一元二次方程![]() 的两个根分别是矩形的边长,则矩形对角线长为______.
的两个根分别是矩形的边长,则矩形对角线长为______.
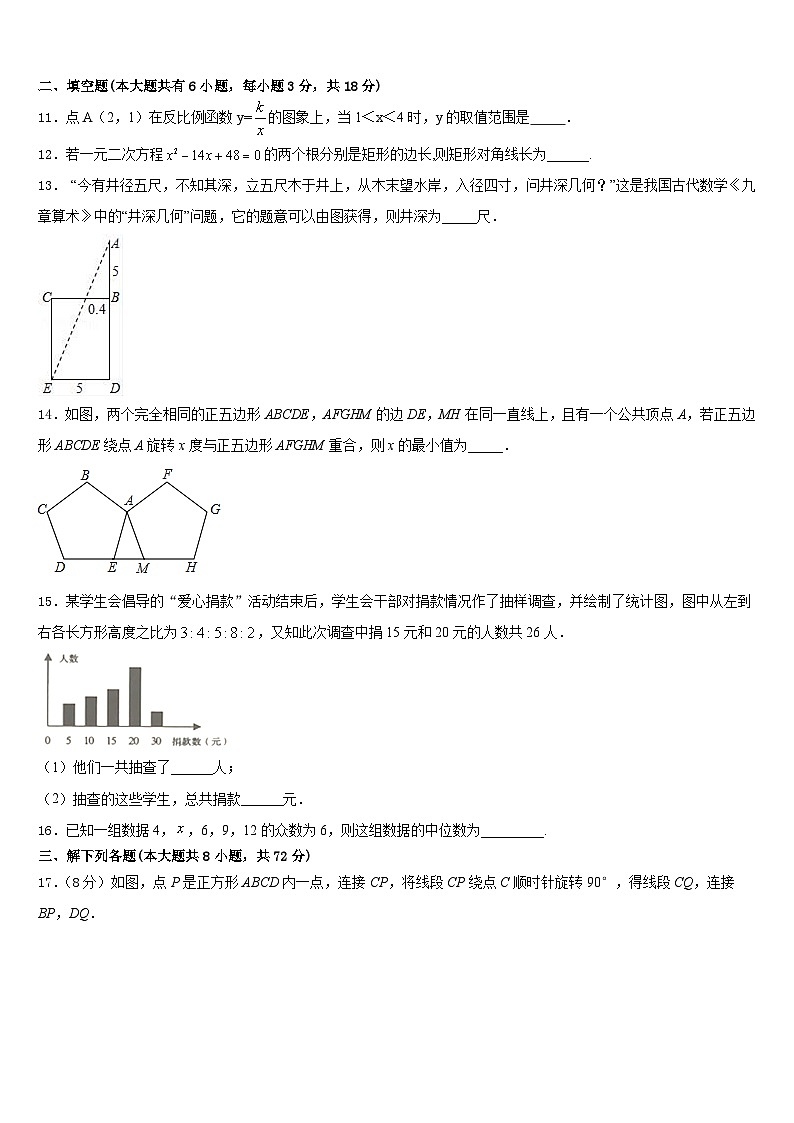
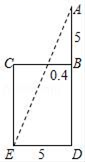
13. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为_____尺.
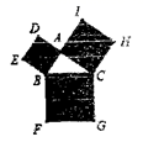
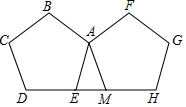
14.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一直线上,且有一个公共顶点A,若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合,则x的最小值为_____.
15.某学生会倡导的“爱心捐款”活动结束后,学生会干部对捐款情况作了抽样调查,并绘制了统计图,图中从左到右各长方形高度之比为![]() ,又知此次调查中捐15元和20元的人数共26人.
,又知此次调查中捐15元和20元的人数共26人.
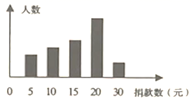
(1)他们一共抽查了______人;
(2)抽查的这些学生,总共捐款______元.
16.已知一组数据4,![]() ,6,9,12的众数为6,则这组数据的中位数为_________.
,6,9,12的众数为6,则这组数据的中位数为_________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,点P是正方形ABCD内一点,连接CP,将线段CP绕点C顺时针旋转90°,得线段CQ,连接BP,DQ.
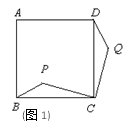
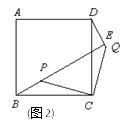
(1)求证:△BCP≌△DCQ;
(2)延长BP交直线DQ于点E.
①如图2,求证:BE⊥DQ;
②若△BCP是等边三角形,请画出图形,判断△DEP的形状,并说明理由.
18.(8分)目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共![]() 只,这两种节能灯的进价、售价如下表:
只,这两种节能灯的进价、售价如下表:
| 进价(元/只) | 售价(元/只) |
甲型 |
|
|
乙型 |
|
|
(1)如何进货,进货款恰好为![]() 元?
元?
(2)设商场购进甲种节能灯![]() 只,求出商场销售完节能灯时总利润
只,求出商场销售完节能灯时总利润![]() 与购进甲种节能灯
与购进甲种节能灯![]() 之间的函数关系式;
之间的函数关系式;
(3)如何进货,商场销售完节能灯时获利最多且不超过进货价的![]() ,此时利润为多少元?
,此时利润为多少元?
19.(8分)解不等式组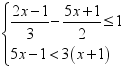 并在数轴上表示出不等式组的解集.
并在数轴上表示出不等式组的解集.
20.(8分)如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD.
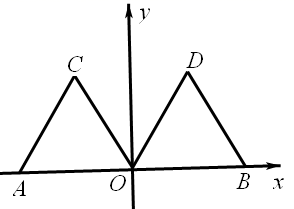
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数.
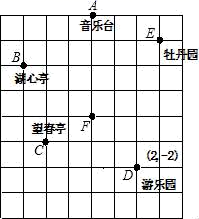
21.(8分)小倩和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴;只知道游乐园D的坐标为(2,﹣2).
(1)画出平面直角坐标系;
(2)求出其他各景点的坐标.
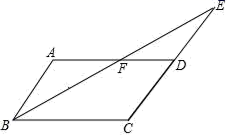
22.(10分)如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF,
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
23.(10分)某中学积极开展跳绳锻炼,一次体育測试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和頻数分布直方图,如图:
次数 | 频数 |
|
|
| 4 |
| 18 |
| 13 |
| 8 |
|
|
| 1 |
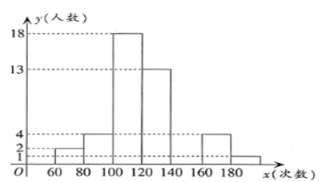
(1)补全频数分布表和频数分布直方图;
(2)表中组距是 次,组数是 组;
(3)跳绳次数在![]() 范围的学生有 人,全班共有 人;
范围的学生有 人,全班共有 人;
(4)若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
24.(12分)如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是1.
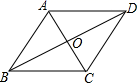
求:(1)两条对角线的长度;(2)菱形的面积.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、B
5、C
6、C
7、B
8、C
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() <y<1
<y<1
12、1
13、57.5
14、144°.
15、1, 2.
16、1
三、解下列各题(本大题共8小题,共72分)
17、(1)证明见解析;(2)①证明见解析;②作图见解析;△DEP为等腰直角三角形,理由见解析.
18、(1)乙型节能灯为800; (2)![]()
![]() ; (3)购进乙型节能灯
; (3)购进乙型节能灯![]() 只时的最大利润为
只时的最大利润为![]() 元.
元.
19、-1≤x<2
20、(1)2;y轴;120(2)90°
21、A(0,4),B(﹣3,2),C(﹣2,﹣1),E(3,3),F(0,0).
22、①见解析②1
23、(1)见解析,(2)表中组距是20次,组数是7组;(3)31人,50人;(4)26%
24、(1)AC=8,BD=![]() ;(2)
;(2)![]() .
.
2023-2024学年湖北省武汉第二初级中学九上数学期末学业质量监测模拟试题含答案: 这是一份2023-2024学年湖北省武汉第二初级中学九上数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,如图,AB是⊙O的弦,下列事件中,是必然事件的是等内容,欢迎下载使用。
湖北省武汉市武汉外学校2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份湖北省武汉市武汉外学校2022-2023学年七下数学期末学业质量监测模拟试题含答案,共6页。试卷主要包含了下列结论中正确的有,一个正比例函数的图象经过等内容,欢迎下载使用。
湖北省武汉市蔡甸区誉恒联盟2022-2023学年七年级数学第二学期期末学业质量监测试题含答案: 这是一份湖北省武汉市蔡甸区誉恒联盟2022-2023学年七年级数学第二学期期末学业质量监测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,已知一次函数y=kx+b等内容,欢迎下载使用。












