2022-2023学年湖北省宜昌西陵区五校联考数学七下期末统考试题含答案

2022-2023学年湖北省宜昌西陵区五校联考数学七下期末统考试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．如果成立，那么实数a的取值范围是(    )

A． B． C． D．

2．化简：（    ）

A．2 B．-2 C．4 D．-4

3．如图1，在矩形ABCD中，动点E从点B出发，沿BADC方向运动至点C处停止，设点E运动的路程为x，△BCE的面积为y，如果y关于x的函数图象如图2所示，则矩形ABCD的周长为（　　）

A．20 B．21 C．14 D．7

4．计算的结果为（ ）

A． B． C．3 D．5

5．四边形的对角线互相平分，要使它变为矩形，需要添加的条件是（ ）

A．AB=CD B．AC=BD

C．AB=BC D．AD=BC

6．下面图形中是中心对称但不一定是轴对称图形的是       （　 　）

A．平行四边形    B．长方形    C．菱形    D．正方形

7．在平行四边形ABCD中，对角线AC，BD相交于点O． 下列条件不能判定平行四边形ABCD为矩形的是(　 　)

A．∠ABC＝90° B．AC＝BD

C．AC⊥BD D．∠BAD＝∠ADC

8．某校将举办一场“中国汉字听写大赛”，要求每班推选一名同学参加比赛，为此，初二(1)班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学的平均分都是96分，甲的成绩的方差是0.3，乙的成绩的方差是0.4，根据以上数据，下列说法正确的是(   )

A．甲的成绩比乙的成绩稳定

B．乙的成绩比甲的成绩稳定

C．甲、乙两人的成绩一样稳定

D．无法确定甲、乙的成绩谁更稳定

9．如图，两个连接在一起的菱形的边长都是1cm，一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行，当电子甲虫爬行2014cm时停下，则它停的位置是(　   　)

A．点F B．点E C．点A D．点C

10．在▱ABCD中，∠A+∠C=130°，则∠A的度数是（　　）

A．50° B．65° C．70° D．80°

11．体育课上，某班三名同学分别进行了6次短跑训练，要判断哪一名同学的短跑成绩比较稳定，通常需要比较三名同学短跑成绩的 （    ）

A．平均数 B．频数 C．方差 D．中位数

12．如图，顺次连接四边形ABCD各边的中点的四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（   ）

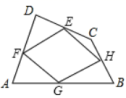
A．AB∥DC B．AC=BD C．AC⊥BD D．AB=CD

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．若整数m满足，且，则m的值为___________.

14．若，则a与b的大小关系为a_____b(填“＞”、“＜”或“=”)

15．在平面直角坐标系中，点A（x，y）在第三象限，则点B（x，﹣y）在第_____象限．

16．如图，在矩形ABCD中，DE⊥AC，∠CDE=2∠ADE，那么∠BDC的度数是________．

17．如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠EPF=147°，则∠PFE的度数是___．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，将▱ABCD的边AB延长到点E，使，DE交边BC于点F．

求证：；

若，求证：四边形BECD是矩形．

19．（5分）已知y是x的函数，自变量x的取值范围是，下表是y与x的几组对应值．

小华根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．下面是小华的探究过程，请将其补充完整：

（1）如图，在平面直角坐标系xOy中，描出了以上表中各组对应值为坐标的点．根据描出的点，画出该函数的图象．

（2）根据画出的函数图象，写出：

①时，对应的函数值y约为          （结果精确到0.01）；

②该函数的一条性质：                                                  ．

20．（8分）一个批发兼零售的文具店规定：凡一次购买铅笔300枝以上，（不包括300枝），可以按批发价付款，购买300枝以下，（包括300枝）只能按零售价付款．小明来该店购买铅笔，如果给八年级学生每人购买1枝，那么只能按零售价付款，需用120元，如果购买60枝，那么可以按批发价付款，同样需要120元，

（1）  这个八年级的学生总数在什么范围内？

（2）  若按批发价购买6枝与按零售价购买5枝的款相同，那么这个学校八年级学生有多少人？

21．（10分）在正方形中，过点A引射线，交边于点H（H不与点D重合）．通过翻折，使点B落在射线上的点G处，折痕交于E，连接E，G并延长交于F．

（1）如图1，当点H与点C重合时，与的大小关系是_________；是____________三角形.

（2）如图2，当点H为边上任意一点时（点H与点C不重合）．连接，猜想与的大小关系，并证明你的结论．

（3）在图2，当，时，求的面积．

22．（10分）选择合适的点，在如图所示的坐标系中描点画出函数的图象，并指出当为何值时，的值大于1．

23．（12分）学校准备从甲乙两位选手中选择一位参加汉字听写大赛，学校对两位选手的表达能力、阅读理解、综合素质和汉字听写四个方面做了测试，他们的各项成绩（百分制）如表：

如果表达能力、阅读理解、综合素质和汉字听写成绩按照2：1：3：4的比确定，请分别计算两名选手的平均成绩，从他们的成绩看，应选派谁？

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、B

2、A

3、C

4、C

5、B

6、A

7、C

8、A

9、A

10、B

11、C

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、，，．

14、=

15、二

16、30°

17、16.5°

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）证明见解析；（2）证明见解析.

19、（1）见解析；（2）①-2.01（答案不唯一）；②y随x的增大而增大（答案不唯一）

20、（1）240人＜八年级学生数≤300人

（2）这个学校八年级学生有300人．

21、（1）；等腰直角．（2）详见解析；（3）

22、图象见详解；时，．

23、应派乙去