


2022-2023学年浙江省台州黄岩区六校联考数学七年级第二学期期末达标检测试题含答案
展开2022-2023学年浙江省台州黄岩区六校联考数学七年级第二学期期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.点![]() 到
到![]() 轴的距离为( )
轴的距离为( )
A.3 B.4 C.5 D.![]()
2.如图,![]() 沿直线边BC所在的直线向右平移得到
沿直线边BC所在的直线向右平移得到![]() ,下列结论中不一定正确的是
,下列结论中不一定正确的是![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.下列各式从左到右的变形属于因式分解的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元.设每半年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )
A.438(1+x)2=389 B.389(1+x)2=438
C.389(1+2x)=438 D.438(1+2x)=389
5.估计(![]() +3
+3![]() )×
)×![]() 的运算结果应在( )之间.
的运算结果应在( )之间.
A.2和3 B.3和4 C.4和5 D.5和6
6.如图,OC平分∠AOB,点P是射线OC上的一点,PD⊥OB于点D,且PD=3,动点Q在射线OA上运动,则线段PQ的长度不可能是( )
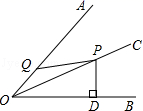
A.2 B.3 C.4 D.5
7.在平面直角坐标系中,函数y=﹣2x+|a|+1的大致图象是( )
A.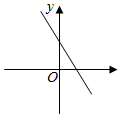 B.
B.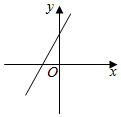
C.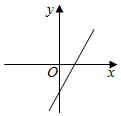 D.
D.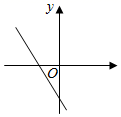
8.若不等式组![]() ,只有三个正整数解,则a的取值范围为( )
,只有三个正整数解,则a的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图所示,“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是![]() ”,这种说明问题的方式体现的数学思想方法叫做( )
”,这种说明问题的方式体现的数学思想方法叫做( )
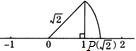
A.代入法 B.换元法 C.数形结合 D.分类讨论
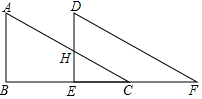
10.《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.书中有下列问題:“今有邑方不知大小,各中开门,出北门八十步有木,出西门二百四十五步见木,问邑方有几何?”意思是:如图,点![]() 、点
、点![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 过点
过点![]() ,
,![]() 步,
步,![]() 步,则正方形的边长为( )
步,则正方形的边长为( )
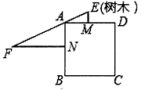
A.![]() 步 B.
步 B.![]() 步 C.
步 C.![]() 步 D.
步 D.![]() 步
步
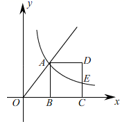
11.如图,![]() 是射线
是射线![]() 上一点,过
上一点,过![]() 作
作![]() 轴于点
轴于点![]() ,以
,以![]() 为边在其右侧作正方形
为边在其右侧作正方形![]() ,过
,过![]() 的双曲线
的双曲线![]() 交
交![]() 边于点
边于点![]() ,则
,则![]() 的值为
的值为![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
12.已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是( )
A.3 B.4 C.5 D.6
二、填空题(每题4分,满分20分,将答案填在答题纸上)
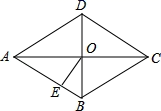
13.如图所示,在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() .OE⊥AB,垂足为
.OE⊥AB,垂足为![]() ,若
,若![]() ,则
,则![]() 的大小为____________.
的大小为____________.
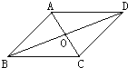
14.如图已知四边形ABCD中,AB=CD,AB//CD要使四边形ABCD是菱形,应添加的条件是_____________________________(只填写一个条件,不使用图形以外的字母).
15.如果直线 y=-2x+k 与两坐标轴所围成的三角形面积是 9,则 k的值为_____.
16.矩形、菱形和正方形的对角线都具有的性质是_____.
17.不等式9﹣3x>0的非负整数解的和是_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
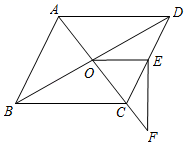
18.(5分)如图,O是平行四边形ABCD对角线AC、BD的交点,E是CD的中点,EF⊥OE交AC延长线于F,若∠ACB=50°,求∠F的度数.
19.(5分)已知BD是△ABC的角平分线,ED⊥BC,∠BAC=90°,∠C=30°.
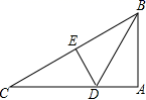
(1)求证:CE=BE;
(2)若AD=3,求△ABC的面积.
20.(8分)如图,在平面直角坐标系中,直线y=![]() x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
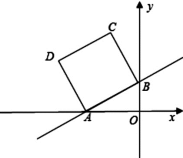
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)在x轴上找一点M,使△MDB的周长最小,请求出M点的坐标.
21.(10分)如图,四边形![]() 是菱形,对角线
是菱形,对角线![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() .
.
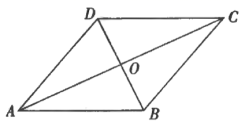
(1)菱形![]() 的周长为 ;
的周长为 ;
(2)若![]() ,求
,求![]() 的长.
的长.
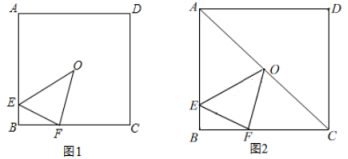
22.(10分)如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.
23.(12分)某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月底统计知三月份的销量达到了500件.
(1)求二、三月份服装销售量的平均月增长率;
(2)从四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、C
3、D
4、B
5、C
6、A
7、A
8、A
9、C
10、A
11、A
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、65°
14、AC![]() BD,或AB=AD(答案不唯一)
BD,或AB=AD(答案不唯一)
15、±1.
16、对角线互相平分
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、∠F的度数是40°.
19、(1)见解析;(2)△ABC的面积=![]() .
.
20、(1)![]() ;(2)D(-6,4);(3)M(-2,0)
;(2)D(-6,4);(3)M(-2,0)
21、 (1)1; (2)AC=![]()
22、(1)45°;(2)证明见解析;(3)![]()
23、(1)二、三月份销售量的平均月增长率为25%;(2)每件降价50元,四月份可获利12000元.
2023-2024学年浙江省台州黄岩区六校联考数学九上期末质量跟踪监视试题含答案: 这是一份2023-2024学年浙江省台州黄岩区六校联考数学九上期末质量跟踪监视试题含答案,共8页。试卷主要包含了下列判断正确的是,如图图形中,是中心对称图形的是,如果,那么的值为,若将抛物线y=2等内容,欢迎下载使用。
2023-2024学年浙江省台州黄岩区六校联考九上数学期末质量检测试题含答案: 这是一份2023-2024学年浙江省台州黄岩区六校联考九上数学期末质量检测试题含答案,共7页。
浙江省台州黄岩区六校联考2023-2024学年八年级数学第一学期期末预测试题含答案: 这是一份浙江省台州黄岩区六校联考2023-2024学年八年级数学第一学期期末预测试题含答案,共8页。试卷主要包含了的平方根与-8的立方根之和是,下列语句正确的是,若关于x的方程无解,则a的值是等内容,欢迎下载使用。












