


2022-2023学年江西育华学校数学七下期末调研试题含答案
展开2022-2023学年江西育华学校数学七下期末调研试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
平均数(环) | 9. 3 | 9. 3 | 9. 3 | 9. 3 |
方差 | 0. 025 | 0. 015 | 0. 035 | 0. 023 |
则这四人中成绩发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.一次函数![]() 在平面直角坐标系内的图像如图所示,则k和b的取值范围是( )
在平面直角坐标系内的图像如图所示,则k和b的取值范围是( )
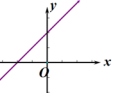
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
3.如图,在矩形ABCD中对角线AC、BD相交于点O,∠ACB=60°,则∠AOB的大小为( )
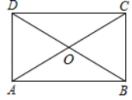
A.30° B.60° C.120° D.150°
4.如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )
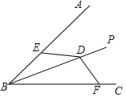
A.40° B.50° C.60° D.70°
5.甲、乙、丙、丁四名射击选手,在相同条件下各射靶10次,他们的成绩统计如下表所示,
若要从他们中挑选一位成绩最高且波动较小的选手参加射击比赛,那么一般应选( )
| 甲 | 乙 | 丙 | 丁 |
平均数(环) | 9 | 9.5 | 9 | 9.5 |
方差 | 3.5 | 4 | 4 | 5.4 |
A.甲 B.乙 C.丙 D.丁
6.如图,在平面直角坐标系中,点![]() 是直线
是直线![]() 上一点,过
上一点,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]()
![]() ,依次作下去,若点
,依次作下去,若点![]() 的纵坐标是1,则
的纵坐标是1,则![]() 的纵坐标是( ).
的纵坐标是( ).
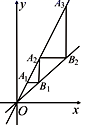
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
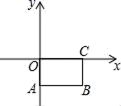
A.(4,2) B.(﹣2,4) C.(4,﹣2) D.(﹣4,2)
8.点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.当S=12时,则点P的坐标为( )
A.(6,2) B.(4,4) C.(2,6) D.(12,﹣4)
9.已知点P(a,3+a)在第二象限,则a的取值范围是( )
A.a<0 B.a>﹣3 C.﹣3<a<0 D.a<﹣3
10.如图,图中的四边形都是正方形,三角形都是直角三角形,其中正方形的面积分别记为A,B,C,D,则它们之间的关系为 ( )
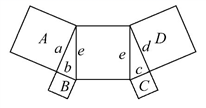
A.A+B=C+D B.A+C=B+D
C.A+D=B+C D.以上都不对
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在平面直角坐标系中,已知点![]() ,直线
,直线![]() 与线段
与线段![]() 有交点,则
有交点,则![]() 的取值范围为__________.
的取值范围为__________.
12.直线![]() 与两坐标轴围成的三角形的面积为4,则
与两坐标轴围成的三角形的面积为4,则![]() 的值为______.
的值为______.
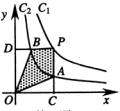
13.如图,两个反比例函数y= ![]() 和y=
和y= ![]() 在第一象限内的图象依次是C2和C1,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为_________.
在第一象限内的图象依次是C2和C1,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为_________.
14.若![]() ,则
,则![]() =_______________.
=_______________.
15.王玲和李凯进行投球比赛,每人连投12次,投中一次记2分,投空一次记1分,王玲先投,投得16分,李凯要想超过王玲,应至少投中________次.
16.4是_____的算术平方根.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在![]() 的网格中,网格线的公共点称为格点.已知格点
的网格中,网格线的公共点称为格点.已知格点![]() 、
、![]() ,如图所示线段
,如图所示线段![]() 上存在另外一个格点.
上存在另外一个格点.
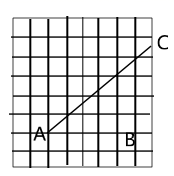
(1)建立平面直角坐标系,并标注![]() 轴、
轴、![]() 轴、原点;
轴、原点;
(2)直接写出线段![]() 经过的另外一个格点的坐标:_____;
经过的另外一个格点的坐标:_____;
(3)用无刻度的直尺画图,运用所学的三角形全等的知识画出经过格点![]() 的射线
的射线![]() ,使
,使![]() (保留画图痕迹),并直接写出点
(保留画图痕迹),并直接写出点![]() 的坐标:_____.
的坐标:_____.
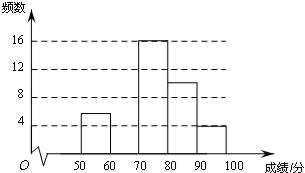
18.(8分)为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 | a | 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | c | b |
合计 | 50 | 1.00 |
(1)表中的a=______,b=______,c=______;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
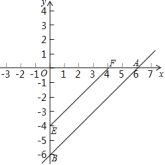
19.(8分)直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF//AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(_____,______),B(______,_____);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?
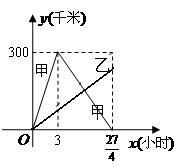
20.(8分)已知:甲、乙两车分别从相距300千米的![]() 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到![]() 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象.
(小时)之间的函数图象.
(1)求甲车离出发地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了![]() 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
21.(8分)如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象有一个交点为
的图象有一个交点为![]() .
.
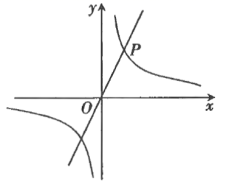
(1)求反比例函数![]() 函数表达式;
函数表达式;
(2)根据图象,直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
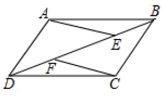
22.(10分)如图,四边形![]() 是平行四边形,
是平行四边形,![]() 、
、![]() 是对角线
是对角线![]() 上的两个点,且
上的两个点,且![]() .求证:
.求证:![]() .
.
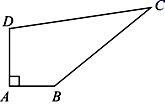
23.(10分)我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?
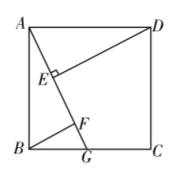
24.(12分)如图,四边形![]() 是正方形,点
是正方形,点![]() 是
是![]() 上的任意一点,
上的任意一点,![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:
.求证:![]()
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、C
4、A
5、B
6、B
7、C
8、B
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]()
13、2
14、36
15、1
16、16.
三、解下列各题(本大题共8小题,共72分)
17、(1)如图所示见解析;(2)(5,4);(3)![]() .
.
18、(1)14;0.08;4;(2)详见解析;(3)80.
19、(1)①6,0,0,-6;②见详解;(2)证明见详解,当![]() 时,四边形DHEF为菱形;(3)四边形ABCD是矩形,当
时,四边形DHEF为菱形;(3)四边形ABCD是矩形,当![]() 时,四边形ABCD的面积为1.
时,四边形ABCD的面积为1.
20、见解析
21、(1)![]() ;(1)
;(1)![]() .
.
22、见解析
23、(1)2;(2)7200元.
24、见详解.
2023-2024学年江西育华学校数学九上期末调研试题含答案: 这是一份2023-2024学年江西育华学校数学九上期末调研试题含答案,共7页。试卷主要包含了某班7名女生的体重,一元二次方程的根的情况为,已知,则代数式的值为,在中,,,,则的值为等内容,欢迎下载使用。
2023-2024学年江西育华学校数学八上期末联考模拟试题含答案: 这是一份2023-2024学年江西育华学校数学八上期末联考模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,在实数,,,中,无理数是,在,,,,中,是分式的有等内容,欢迎下载使用。
2023-2024学年江西省育华学校八上数学期末预测试题含答案: 这是一份2023-2024学年江西省育华学校八上数学期末预测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列分式中,是最简分式的是等内容,欢迎下载使用。












